
Concept explainers
a.
To find: Plot the graph and the analyze the various features of the graph.
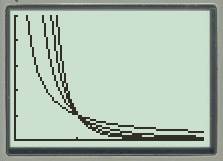
The graph of the functions is shown below.
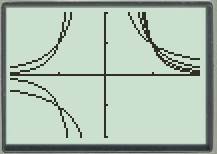
The analysis of the graph is as follows:
| Domain | ||||
| Range | ||||
| Continuous | Yes | Yes | Yes | Yes |
| Increasing | ||||
| Decreasing | ||||
| Symmetry | Origin | Y-axis | Origin | Y-axis |
| Bounded | Not bounded | Below | Not bounded | Below |
| Extrema | No | No | No | No |
| Asymptotes | ||||
| End behavior |
Given:
The functions are
Calculation:
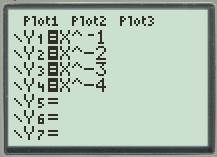
First of all plot all the functions
Press the
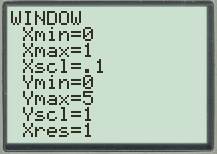
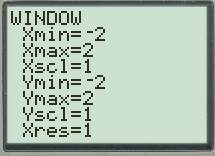
Set up the graphing window.
Press the
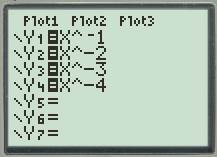
Next plot all the functions
Press the
Set up the graphing window.
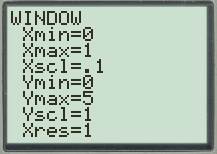
Press the
Next plot all the functions
Press the
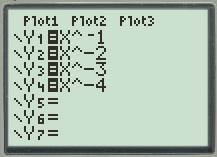
Set up the graphing window.
Press the
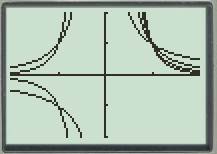
The analysis of the graphs is shown as below.
| Domain | ||||
| Range | ||||
| Continuous | Yes | Yes | Yes | Yes |
| Increasing | ||||
| Decreasing | ||||
| Symmetry | Origin | Y-axis | Origin | Y-axis |
| Bounded | Not bounded | Below | Not bounded | Below |
| Extrema | No | No | No | No |
| Asymptotes | ||||
| End behavior |
b.
To find: Plot the graph and the analyze the various features of the graph.
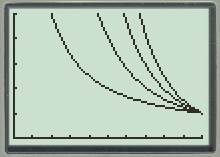
The graph of the functions is shown below.
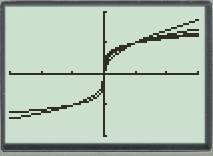
The analysis of the graph is as follows:
| Domain | ||||
| Range | ||||
| Continuous | Yes | Yes | Yes | Yes |
| Increasing | ||||
| Decreasing | ||||
| Symmetry | Origin | Y-axis | Origin | Y-axis |
| Bounded | Not bounded | Below | Not bounded | Below |
| Extrema | No | No | No | No |
| Asymptotes | ||||
| End behavior |
Given:
The functions are
Calculation:
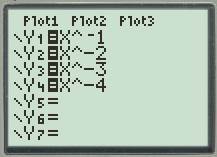
First of all plot all the functions
Press the
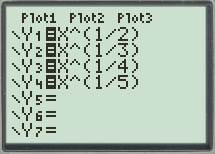
Set up the graphing window.
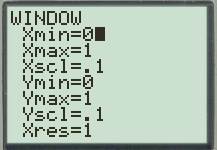
Press the
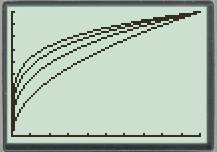
Next plot all the functions
Press the
Set up the graphing window.
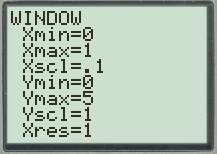
Press the
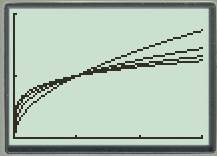
Next plot all the functions
Press the

Set up the graphing window.
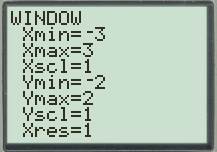
Press the
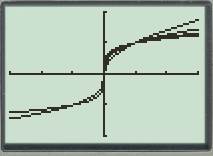
The analysis of the graphs is shown as below.
| Domain | ||||
| Range | ||||
| Continuous | Yes | Yes | Yes | Yes |
| Increasing | ||||
| Decreasing | ||||
| Symmetry | Origin | Y-axis | Origin | Y-axis |
| Bounded | Not bounded | Below | Not bounded | Below |
| Extrema | No | No | No | No |
| Asymptotes | ||||
| End behavior |
Chapter 2 Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





