Chapter 2.8, Problem 60E

Solution

To find: The arc of length $x$ .

The arc length is less than $11.1$ inches.

Given information:

Cone Problem Beginning with a circular piece of paper with a $4-$ inches radius, as shown in (a), cut out a sector with an arc of length $x$ .

Join the two radical edges of the remaining portion of the paper to form a cone with radius $r$ and height $h$, as shown in (b):

  

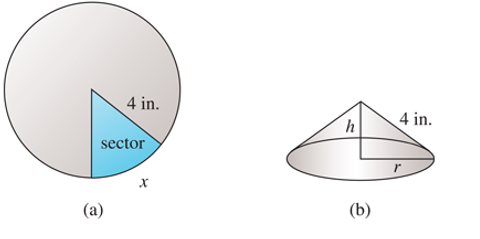
Calculation:

From the figure (a):

The circumference of a circle with radius $4-$ inches is:

  $\begin{array}{c}C=2\pi \times 4\\ =8\pi \end{array}$

Since the circumference of the base of the cone is equal to the arc length of the remainder of the circle, the circumference is $8\pi -x$ .

From the figure (b):

Since the radius of the base of the cone is $r$ , so the circumference of the base of the cone can be written as below:

  $8\pi -x=2\pi r$

Solve for $r$ :

  $\begin{array}{c}8\pi -2\pi r=x\\ 2\pi \left(4-r\right)=x\\ 4-r=\frac{x}{2\pi }\\ r=4-\frac{x}{2\pi }\end{array}$

In the figure (a), the radius $r$ , the height $h$ and the slant height $4$ make a right triangle.

Use the Pythagorean Theorem and calculate the value of $h$ below:

  $\begin{array}{c}{h}^2+r^2=4^2\\ h^2+{\left(4-\frac{x}{2\pi }\right)}^2=16\\ h^2+16+\frac{x^2}{4{\pi }^2}-\frac{4x}{\pi }=16\\ h^2+\frac{x^2}{4{\pi }^2}-\frac{4x}{\pi }=0\\ h^2=\frac{4x}{\pi }-\frac{x^2}{4{\pi }^2}\\ h=\sqrt{\frac{4x}{\pi }-\frac{x^2}{4{\pi }^2}}\end{array}$

Now, the volume of the cone is $V=\frac{1}{3}\pi r^{2}h$ .

Since the volume of the cone is greater than $21$ in³.

Therefore, the volume can be written in inequality below:

  $\frac{1}{3}\pi {\left(4-\frac{x}{2\pi }\right)}^2\left(\sqrt{\frac{4x}{\pi }-\frac{x^2}{4{\pi }^2}}\right)>21$

Solve for $x$ :

  $\begin{array}{l}\pi {\left(4-\frac{x}{2\pi }\right)}^2\left(\sqrt{\frac{4x}{\pi }-\frac{x^2}{4{\pi }^2}}\right)>63\\ \pi {\left(\frac{8\pi -x}{2\pi }\right)}^2\left(\sqrt{\frac{16\pi x-x^2}{4{\pi }^2}}\right)>63\\ \pi \frac{{\left(8\pi -x\right)}^2}{4{\pi }^2}\frac{\sqrt{16\pi x-x^2}}{2\pi }>63\\ \frac{{\left(8\pi -x\right)}^2}{8{\pi }^2}\sqrt{16\pi x-x^2}>63\end{array}$

Since the arc length $x$ cannot be greater than the circumference of the circle, so $0<x<8\pi$ . Therefore,

  $\begin{array}{c}\frac{{\left(8\pi -x\right)}^2}{8{\pi }^2}\times 8\pi >63\\ \frac{{\left(8\pi -x\right)}^2}{\pi }>63\\ {\left(8\pi -x\right)}^2>63\pi \\ 8\pi -x>\pm \sqrt{63\pi }\\ x<8\pi \pm \sqrt{63\pi }\end{array}$

Since the arc length $x$ is $0<x<8\pi$ , so ignore the positive sign.

Therefore,

  $\begin{array}{l}x<8\pi -\sqrt{63\pi }\\ x<11.1\end{array}$

Hence, the arc length is less than $11.1$ inches.