Fundamentals of Heat and Mass Transfer
7th Edition
ISBN: 9780470917855
Author: Bergman, Theodore L./
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2, Problem 2.62P
Consider the steady-state temperature distribution within a composite wall composed of Materials A and B.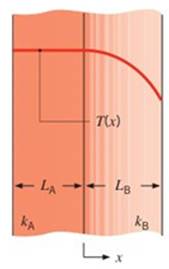 
The conduction process is one-dimensional. Within which material does uniform volumetric generation occur? What is the boundary condition at
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Do fast i will give you good rate
Can you help me with question 3 show all the steps taken.
What is the analogical reason between heat transfer by conduction and flow of electricity through ohmic resistance? Use a composite wall of a building to illustrate the concept. A composite slab with three layers of thermal conductivities k1, k2, k3 and thickness ti, t2, të respectively, are placed in a close contact. Derive an expression from the first principle for the heat flow through the composite slab per unit surface area in terms of the overall temperature difference across the slab.
Chapter 2 Solutions
Fundamentals of Heat and Mass Transfer
Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - Assume steady-state, one-dimensional conduction in...Ch. 2 - A hot water pipe with outside radius r, has a...Ch. 2 - A spherical shell with inner radius r1 and outer...Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - A composite rod consists of two different...Ch. 2 - A solid, truncated cone serves as a support for a...Ch. 2 - To determine the effect of the temperature...Ch. 2 - A young engineer is asked to design a thermal...Ch. 2 - A one-dimensional plane wall of thickness 2L=100mm...
Ch. 2 - Consider steady-state conditions for...Ch. 2 - Consider a plane wall 100 mm thick and of thermal...Ch. 2 - A cylinder of radius ro, length L, and thermal...Ch. 2 - In the two-dimensional body illustrated, the...Ch. 2 - Consider the geometry of Problem 2.14 for the case...Ch. 2 - Steady-state, one-dimensional conduction occurs in...Ch. 2 - An apparatus for measuring thermal conductivity...Ch. 2 - An engineer desires to measure the thermal...Ch. 2 - Consider a 300mm300mm window in an aircraft. For a...Ch. 2 - Consider a small but known volume of metal that...Ch. 2 - Use INT to perform the following tasks. Graph the...Ch. 2 - Calculate the thermal conductivity of air,...Ch. 2 - A method for determining the thermal conductivity...Ch. 2 - Compare and contrast the heat capacity cp of...Ch. 2 - A cylindrical rod of stainless steel is insulated...Ch. 2 - At a given instant of time, the temperature...Ch. 2 - A pan is used to boil water by placing it on a...Ch. 2 - Uniform internal heat generation at q=5107W/m3 is...Ch. 2 - Consider a one-dimensional plane wall with...Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - The temperature distribution across a wall 0.3 m...Ch. 2 - Prob. 2.33PCh. 2 - One-dimensional, steady-state conduction with...Ch. 2 - Derive the heat diffusion equation, Equation 2.26,...Ch. 2 - Derive the heat diffusion equation, Equation 2.29....Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - Prob. 2.41PCh. 2 - Prob. 2.42PCh. 2 - cylindrical system illustrated has negligible...Ch. 2 - Beginning with a differential control volume in...Ch. 2 - Prob. 2.45PCh. 2 - Prob. 2.46PCh. 2 - For a long circular tube of inner and outer radii...Ch. 2 - Passage of an electric current through a long...Ch. 2 - Two-dimensional. steady-state conduction occurs in...Ch. 2 - An electric cable of radius r1 and thermal...Ch. 2 - A spherical shell of inner and outer radii ri and...Ch. 2 - A chemically reacting mixture is stored in a...Ch. 2 - A thin electrical heater dissipating 4000W/m2 is...Ch. 2 - The one-dimensional system of mass M with constant...Ch. 2 - Consider a one-dimensional plane wall of thickness...Ch. 2 - A large plate of thickness 2L is at a uniform...Ch. 2 - The plane wall with constant properties and no...Ch. 2 - Consider the steady-state temperature...Ch. 2 - A plane wall has constant properties, no internal...Ch. 2 - A plane wall with constant properties is initially...Ch. 2 - Consider the conditions associated with Problem...Ch. 2 - Consider the steady-state temperature distribution...Ch. 2 - A spherical particle of radius r1 experiences...Ch. 2 - Prob. 2.64PCh. 2 - A plane wall of thickness L=0.1m experiences...Ch. 2 - Prob. 2.66PCh. 2 - A composite one-dimensional plane wall is of...Ch. 2 - Typically, air is heated in a hair dryer by...Ch. 2 - Prob. 2.69P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A square silicon chip 7mm7mm in size and 0.5-mm thick is mounted on a plastic substrate as shown in the sketch below. The top surface of the chip is cooled by a synthetic liquid flowing over it. Electronic circuits on the bottom of the chip generate heat at a rate of 5 W that must be transferred through the chip. Estimate the steady-state temperature difference between the front and back surfaces of the chip. The thermal conductivity of silicon is 150 W/m K. Problem 1.6arrow_forward1.3 A furnace wall is to be constructed of brick having standard dimensions of Two kinds of material are available. One has a maximum usable temperature of 1040°C and a thermal conductivity of 1.7 W/(m K), and the other has a maximum temperature limit of 870°C and a thermal conductivity of 0.85 W/(m K). The bricks have the same cost and are laid in any manner, but we wish to design the most economical wall for a furnace with a temperature of 1040°C on the hot side and 200°C on the cold side. If the maximum amount of heat transfer permissible is 950 , determine the most economical arrangement using the available bricks.arrow_forwardA section of a composite wall with the dimensions shown below has uniform temperatures of 200C and 50C over the left and right surfaces, respectively. If the thermal conductivities of the wall materials are: kA=70W/mK,kB=60W/mK, kC=40W/mK, and kP=20W/mK, determine the rate of heat transfer through this section of the wall and the temperatures at the interfaces. Repeat Problem 1.34, including a contact resistance of 0.1 K/W at each of the interfaces.arrow_forward
- 5.10 Experiments have been performed on the temperature distribution in a homogeneous long cylinder (0.1 m diameter, thermal conductivity of 0.2 W/m K) with uniform internal heat generation. By dimensional analysis, determine the relation between the steady-state temperature at the center of the cylinder , the diameter, the thermal conductivity, and the rate of heat generation. Take the temperature at the surface as your datum. What is the equation for the center temperature if the difference between center and surface temperature is when the heat generation is ?arrow_forward1.4 To measure thermal conductivity, two similar 1-cm-thick specimens are placed in the apparatus shown in the accompanying sketch. Electric current is supplied to the guard heater, and a wattmeter shows that the power dissipation is 10 W. Thermocouples attached to the warmer and to the cooler surfaces show temperatures of 322 and 300 K, respectively. Calculate the thermal conductivity of the material at the mean temperature in W/m K. Problem 1.4arrow_forwardPlease help me answer question 1, show all the steps taken.arrow_forward
- solve this question completlyarrow_forwardA very long, rectangular cross-section block is made from metal with the following properties: thermal conductivity = 130 W/mK, density = 2771 kg/m³, and specific heat capacity = 703 J/kgK. Initially all 4 sides of the cross section are maintained at 373 K. Then the temperature of one side is suddenly increased to 473 K. The temperature profile in the block will be investigated using an explicit finite difference model. If the time step is fixed at 5.5 seconds, what is the limit for node spacing that should be used to ensure stability of the solution? Give your numerical answer in mm to 1 decimal place.arrow_forwardlook into the attached filearrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Understanding Conduction and the Heat Equation; Author: The Efficient Engineer;https://www.youtube.com/watch?v=6jQsLAqrZGQ;License: Standard youtube license