Fundamentals of Heat and Mass Transfer
7th Edition
ISBN: 9780470917855
Author: Bergman, Theodore L./
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2, Problem 2.5P
Assume steady-state, one-dimensional heat conduction through the symmetric shape shown.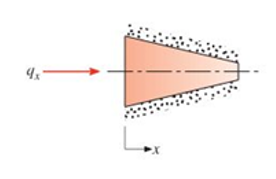 
Assuming that there is no internal heat generation, derive an expression for the thermal conductivity
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Pb 9) 4.44
bas gnibus& WX 002 grillimatul fred
bail (e)
For the simply supported I-beam, a load of 1000 lb in center. Find the maximum transverse shear
stress. Compare your answer with the approximation obtained by dividing the shear load by the
area of the web only with the web considered to extend for the full 8-in depth.
-
3½ in.
12
bas in 0% to tolerabib tormi no grived
in.
8 in.
38
in.
12
½ in.
Pb 12) 4.61
Draw the Mohr circle for the stresses experienced by the surface of an internally pressurized
steel tube that is subject to the tangential and axial stresses in the outer surface of 45 ksi and 30
ksi, respectively, and a torsional stress of 18 ksi.
yx
18
45
30
Pb 8) 4.39
For the C-clamp shown, what force F can be exerted by the screw if the maximum tensile stress
in the clamp is to be limited to 30 ksi?
F
2 in.
სის
3436
16
13
blos 0101 alos12 nodus 121A (s
3 in.
in.
16 in.
16
web
leonas OFF elson yollA (d
016 (& d
of bolow-bloo ai 15912 020112LA
sue) vilisub 22 bal.90
Swman a bris ctxibasqqA) laste is tools?
Chapter 2 Solutions
Fundamentals of Heat and Mass Transfer
Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - Assume steady-state, one-dimensional conduction in...Ch. 2 - A hot water pipe with outside radius r, has a...Ch. 2 - A spherical shell with inner radius r1 and outer...Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - A composite rod consists of two different...Ch. 2 - A solid, truncated cone serves as a support for a...Ch. 2 - To determine the effect of the temperature...Ch. 2 - A young engineer is asked to design a thermal...Ch. 2 - A one-dimensional plane wall of thickness 2L=100mm...
Ch. 2 - Consider steady-state conditions for...Ch. 2 - Consider a plane wall 100 mm thick and of thermal...Ch. 2 - A cylinder of radius ro, length L, and thermal...Ch. 2 - In the two-dimensional body illustrated, the...Ch. 2 - Consider the geometry of Problem 2.14 for the case...Ch. 2 - Steady-state, one-dimensional conduction occurs in...Ch. 2 - An apparatus for measuring thermal conductivity...Ch. 2 - An engineer desires to measure the thermal...Ch. 2 - Consider a 300mm300mm window in an aircraft. For a...Ch. 2 - Consider a small but known volume of metal that...Ch. 2 - Use INT to perform the following tasks. Graph the...Ch. 2 - Calculate the thermal conductivity of air,...Ch. 2 - A method for determining the thermal conductivity...Ch. 2 - Compare and contrast the heat capacity cp of...Ch. 2 - A cylindrical rod of stainless steel is insulated...Ch. 2 - At a given instant of time, the temperature...Ch. 2 - A pan is used to boil water by placing it on a...Ch. 2 - Uniform internal heat generation at q=5107W/m3 is...Ch. 2 - Consider a one-dimensional plane wall with...Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - The temperature distribution across a wall 0.3 m...Ch. 2 - Prob. 2.33PCh. 2 - One-dimensional, steady-state conduction with...Ch. 2 - Derive the heat diffusion equation, Equation 2.26,...Ch. 2 - Derive the heat diffusion equation, Equation 2.29....Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - Prob. 2.41PCh. 2 - Prob. 2.42PCh. 2 - cylindrical system illustrated has negligible...Ch. 2 - Beginning with a differential control volume in...Ch. 2 - Prob. 2.45PCh. 2 - Prob. 2.46PCh. 2 - For a long circular tube of inner and outer radii...Ch. 2 - Passage of an electric current through a long...Ch. 2 - Two-dimensional. steady-state conduction occurs in...Ch. 2 - An electric cable of radius r1 and thermal...Ch. 2 - A spherical shell of inner and outer radii ri and...Ch. 2 - A chemically reacting mixture is stored in a...Ch. 2 - A thin electrical heater dissipating 4000W/m2 is...Ch. 2 - The one-dimensional system of mass M with constant...Ch. 2 - Consider a one-dimensional plane wall of thickness...Ch. 2 - A large plate of thickness 2L is at a uniform...Ch. 2 - The plane wall with constant properties and no...Ch. 2 - Consider the steady-state temperature...Ch. 2 - A plane wall has constant properties, no internal...Ch. 2 - A plane wall with constant properties is initially...Ch. 2 - Consider the conditions associated with Problem...Ch. 2 - Consider the steady-state temperature distribution...Ch. 2 - A spherical particle of radius r1 experiences...Ch. 2 - Prob. 2.64PCh. 2 - A plane wall of thickness L=0.1m experiences...Ch. 2 - Prob. 2.66PCh. 2 - A composite one-dimensional plane wall is of...Ch. 2 - Typically, air is heated in a hair dryer by...Ch. 2 - Prob. 2.69P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Quiz/An eccentrically loaded bracket is welded to the support as shown in Figure below. The load is static. The weld size for weld w1 is h1 = 6mm, for w2 h2 = 5mm, and for w3 is h3 =5.5 mm. Determine the safety factor (S.f) for the welds. F=22 kN. Use an AWS Electrode type (E90xx). 140 S Find the centroid I want university professor solutions O REDMI NOTE 8 PRO CAI QUAD CAMERA 101.15 Farrow_forwardPb 6) 4.31 do = 25 mm 4.31 What bending moment is required to produce a maximum normal stress of 400 MPa: (a) In a straight round rod of 40-mm diameter? (b) In a straight square rod, 40 mm on a side (with bending about the X axis as shown for a rectangular section in Appendix B-2)?arrow_forwardPb 13) 4.73 Find the maximum value of stress at the hole and semicircular notch. 45000 N 50 mm 100 mm 15 mm 25 mm 45000 Narrow_forward
- Pb 11) 4.53 Consider the 1-in solid round shaft supported by self-aligning bearings at A and B. Attached to the shaft are two chain sprockets that are loaded as shown. Treat this as a static loading problem and identify the specific shat location subjected to the most severe state of stress and make a Mohr circle representation of this stress state. 1-in.-dia. shaft 500 lb 2 in. 1000 lb 3 in. 3 in.arrow_forwardPb 5) 4.19 Estimate the torque required to produce a maximum shear stress of 570 MPa in a hollow shaft having an inner diameter of 20 mm and an outer diameter of 25 mm. d; = 20 mm T d = 25 mm Tmax = 570 MPaarrow_forwardQuiz/An eccentrically loaded bracket is welded to the support as shown in Figure below. The load is static. The weld size for weld w1 is h1 = 6mm, for w2 h2 = 5mm, and for w3 is h3 =5.5 mm. Determine the safety factor (S.f) for the welds. F=22 kN. Use an AWS Electrode type (E90xx). I want university professor solutions O REDMI NOTE 8 PRO CAI QUAD CAMERA 140 S 101.15 Farrow_forward
- Research and select different values for the R ratio from various engine models, then analyze how these changes affect instantaneous velocity and acceleration, presenting your findings visually using graphsarrow_forwardMeh Battery operated train Coll CD Af Pair 160,000kg 0.0005 0.15 5m² 1.2kg/m³ 19 7et nong 0.98 0.9 0.88 Tesla Prated Tesla Trated Ywheel ng Jaxle. 270kW 440NM 0.45m 20 2 8.5kgm² Consider a drive cycle of a 500km trip with 3 stops in the middle. Other than the acceleration and deceleration associated with the three stops, the tran maintains. constant cruise speed velocity of 324 km/hr. The tran will fast charge at each stop for 15 min at a rate Peharge = 350 kW (ผม τ (MN 15MIN Stop w charging (350kW GMIJ restored during 15 minutes of fast charging at Calculate the battery energy Pcharge = 350kW Calculate the net energy gain per stop t 64 Determice the total battery energy required Ebat to complete the 500km trip with 3 stops. etcarrow_forwardDO NOT COPY SOLUTION The differential equation of a cruise control system is provided by the following equation: Find the closed loop transfer function with respect to the reference velocity (vr) . a. Find the poles of the closed loop transfer function for different values of K. How does the poles move as you change K? b. Find the step response for different values of K and plot in MATLAB. What can you observe? c. For the given transfer function, find tp, ts, tr, Mp . Plot the resulting step response. G(s) = 40/(s^2 + 4s + 40)arrow_forward
- Aswatan gas occupies a space of 0.3 millike cube at a pressure of 2 bar and temperature of 77 degree Celsius it is indicate at constant volume at pressure of 7 parts determine temperature at the end of process mass of a gas changing internal energy change in enthalpy during the process assume CP is equal to 10 1.005 CV is equal to 0.712 is equal to 287arrow_forwardAUTO CONTROLDNO COPIED ANSWERS, SHOW FULL SOLUTION The differential equation of a DC motor can be described by the following equation Find the transfer function between the applied voltage ( Va)and the motor speed (thetadot m). What is the steady state speed of the motor after a voltage (Va = 10V) has been applied. Find the transfer function between the applied voltage (Va) and the shaft angle (thetadot m) .arrow_forwardAuto Controls DONT COPY ANSWERS Perform the partial fraction expansion of the following transfer function and find the impulse response: G(s) = (s/2 + 5/3) / (s^2 + 4s + 6) G(s) =( 6s^2 + 50) / (s+3)(s^2 +4)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Understanding Conduction and the Heat Equation; Author: The Efficient Engineer;https://www.youtube.com/watch?v=6jQsLAqrZGQ;License: Standard youtube license