Introduction to Heat Transfer
6th Edition
ISBN: 9780470501962
Author: Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, Adrienne S. Lavine
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2, Problem 2.41P
One-dimensional, steady-state conduction with no energy generation is occurring in a plane wall of constant thermal conductivity.
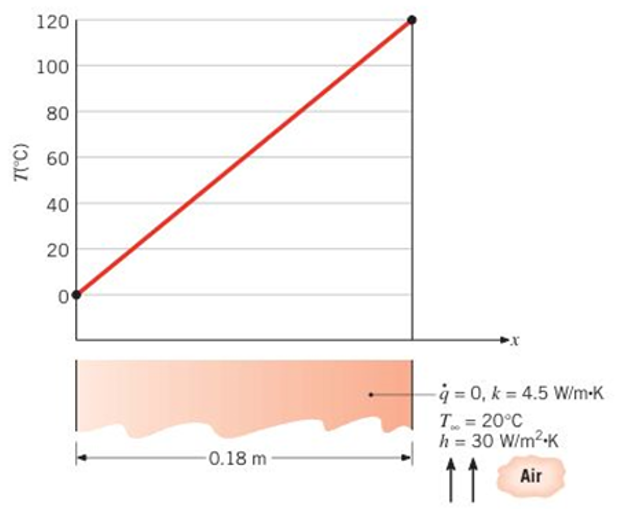
(a) Is the prescribed temperature distribution possible? Briefly explain your reasoning.
(b) With the temperature at
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
1-D, steady-state conduction with uniform internal energy generation occurs in a plane wall with
a thickness of 50 mm and a constant thermal conductivity of 5 W/m/K. The temperature
distribution has the form T = a + bx + cx² °C. The surface at x=0 has a temperature of To =
120 °C and experiences convection with a fluid for which T..
surface at x= 50 mm is well insulated (no heat transfer). Find:
(a) The volumetric energy generation rate q. (15)
(b) Determine the coefficients a, b, and c.
20 °C and h 500 W/m² K. The
To:
= 120°C
T = 20°C
h = 500 W/m².K
111
Fluid
T(x)-
=
q, k = 5 W/m.K
L = 50 mm
A plane wall of thickness 2L = 30 mm and thermal conductivity k = 7 W/m-K experiences uniform volumetric heat generation at a
rate q, while convection heat transfer occurs at both of its surfaces (x = − L, + L), each of which is exposed to a fluid of
temperature T = 20°C. Under steady-state conditions, the temperature distribution in the wall is of the form
T(x) = a + bx + cx² where a = 82.0°C, b = -210°C/m, c = -2x 10°C/m², and x is in meters. The origin of the x-coordinate is at
the midplane of the wall.
(a) What is the volumetric rate à of heat generation in the wall?
(b) Determine the surface heat fluxes, q" (L)and q ( + L).
(c) What are the convection coefficients for the surfaces at x = - Land x = + L?
The volumetric rate of heat generation in the wall, in W/m³:
q = i
W/m³
The surface heat flux, in W/m²:
qx ( - L) = i
The surface heat flux, in W/m²:
q (+ L) = i
W/m²
W/m²
The convection coefficients for the surface at x = - L, in W/m²-K:
h(- L) = i
W/m².K
The convection…
A plane wall of thickness 2L = 2*33 mm and thermal conductivity k = 7 W/m-K experiences uniform volumetric heat generation at a rate q˙, while convection heat transfer occurs at both of its surfaces (x = −L, + L), each of which is exposed to a fluid of temperature T∞ = 31°C. Under steady-state conditions, the temperature distribution in the wall is of the form T(x) = a + bx + cx2 where a = 85°C, b = −-218°C/m, c = −-23,942°C/m2, and x is in meters. The origin of the x-coordinate is at the midplane of the wall.
(a) Sketch the temperature distribution and identify significant physical features.
(b) What is the volumetric rate of heat generation q˙ in the wall?
(c) Obtain an expression for the heat flux distribution qx″(x). Is the heat flux zero at any location? Explain any significant features of the distribution.
(d) Determine the surface heat fluxes, qx″(−L) and qx″(+L). How are these fluxes related to the heat generation rate?
(e) What are the convection coefficients…
Chapter 2 Solutions
Introduction to Heat Transfer
Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - Assume steady-state, one-dimensional conduction in...Ch. 2 - A hot water pipe with outside radius r1 has a...Ch. 2 - A spherical shell with inner radius r1 and outer...Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - A composite rod consists of two different...Ch. 2 - A solid, truncated cone serves as a support for a...Ch. 2 - To determine the effect of the temperature...Ch. 2 - Prob. 2.9PCh. 2 - A one-dimensional plane wall of thickness 2L=100mm...
Ch. 2 - Consider steady-state conditions for...Ch. 2 - Consider a plane wall 100 mm thick and of thermal...Ch. 2 - Prob. 2.13PCh. 2 - In the two-dimensional body illustrated, the...Ch. 2 - Consider the geometry of Problem 2.14 for the case...Ch. 2 - Steady-state, one-dimensional conduction occurs in...Ch. 2 - Prob. 2.17PCh. 2 - Prob. 2.18PCh. 2 - Consider a 300mm300mm window in an aircraft. For a...Ch. 2 - Prob. 2.20PCh. 2 - Use IHT to perform the following tasks. Graph the...Ch. 2 - Calculate the thermal conductivity of air,...Ch. 2 - A method for determining the thermal conductivity...Ch. 2 - Prob. 2.24PCh. 2 - Prob. 2.25PCh. 2 - At a given instant of time, the temperature...Ch. 2 - Prob. 2.27PCh. 2 - Uniform internal heat generation at q.=5107W/m3 is...Ch. 2 - Prob. 2.29PCh. 2 - The steady-state temperature distribution in a...Ch. 2 - The temperature distribution across a wall 0.3 m...Ch. 2 - Prob. 2.32PCh. 2 - Prob. 2.33PCh. 2 - Prob. 2.34PCh. 2 - Prob. 2.35PCh. 2 - Prob. 2.36PCh. 2 - Prob. 2.37PCh. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - Prob. 2.42PCh. 2 - Prob. 2.43PCh. 2 - Prob. 2.44PCh. 2 - Beginning with a differential control volume in...Ch. 2 - A steam pipe is wrapped with insulation of inner...Ch. 2 - Prob. 2.47PCh. 2 - Prob. 2.48PCh. 2 - Two-dimensional, steady-state conduction occurs in...Ch. 2 - Prob. 2.50PCh. 2 - Prob. 2.51PCh. 2 - A chemically reacting mixture is stored in a...Ch. 2 - A thin electrical heater dissipating 4000W/m2 is...Ch. 2 - The one-dimensional system of mass M with constant...Ch. 2 - Consider a one-dimensional plane wall of thickness...Ch. 2 - A large plate of thickness 2L is at a uniform...Ch. 2 - Prob. 2.57PCh. 2 - Prob. 2.58PCh. 2 - A plane wall has constant properties, no internal...Ch. 2 - A plane wall with constant properties is initially...Ch. 2 - Consider the conditions associated with Problem...Ch. 2 - Prob. 2.62PCh. 2 - A spherical particle of radius r1 experiences...Ch. 2 - Prob. 2.64PCh. 2 - A plane wall of thickness L=0.1m experiences...Ch. 2 - Prob. 2.66PCh. 2 - A composite one-dimensional plane wall is of...Ch. 2 - Prob. 2.68PCh. 2 - The steady-state temperature distribution in a...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A plane wall 15 cm thick has a thermal conductivity given by the relation k=2.0+0.0005T[W/mK] where T is in kelvin. If one surface of this wall is maintained at 150C and the other at 50C, determine the rate of heat transfer per square meter. Sketch the temperature distribution through the wall.arrow_forwardA plane wall, 7.5 cm thick, generates heat internally at the rate of 105 W/m3. One side of the wall is insulated, and the other side is exposed to an environment at 90C. The convection heat transfer coefficient between the wall and the environment is 500 W/m2 K. If the thermal conductivity of the wall is 12 W/m K, calculate the maximum temperature in the wall.arrow_forwardA plane wall of thickness 2L has internal heat sources whose strength varies according to qG=qocos(ax) Where qo is the heat generated per unit volume at the center of the wall (x=0) and a is a constant. If both sides of the wall are maintained at a constant temperature of Tw, derive an expression for the total heat loss from the wall per unit surface area.arrow_forward
- 4x F2 # 3 E 4, F3 54 $ R F4 Ac = 1m² ▬ H DII x= 1 m (4) Consider a wall (as shown above) of thickness L-1 m and thermal conductivity k-1 W/m-K. The left (x=0) and the right (x=1 m) surfaces of the wall are subject to convection with a convectional heat transfer coefficient h= 1 W/m²K and an ambient temperature T. 1 K. There is no heat generation inside the wall. You may assume 1-D heat transfer, steady state condition, and neglect any thermal contact resistance. Find T(x). % To,1 = 1 K h₁ = 1 W/m²K 5 Q Search F5 T T₁ A 6 x=0 F6 à = 0 W/m³ k= 1W/mK L=1m Y 994 F7 & 7 T₂ U Ton2 = 1 K h₂ = 1 W/m²K1 PrtScn F8 Page of 7 ) 0 PgUp F11 Parrow_forwardA plane wall of thickness 2L=40 mm and thermal conductivity k=5 W/m·K experiences uniform volumetric heat generation at a rate q, while convection heat transfer occurs at both of its surfaces (x=-L, +L), each of which is exposed to a fluid of temperature T=20 °C. Under steady-state conditions, the temperature distribution in the wall is of the form T(x) = a+bx+cx² where a = 82.0 °C, b=-210 °C/m, c = -2x10 °C/m², and x is in meters. The origin of the x- coordinate is at the midplane of the wall. -L x -L (a) Determine the surface heat fluxes, qx(-L) and qx(+L). (b) What is the volumetric rate of heat generation & in the wall? (c) What is the convection heat transfer coefficient for the surfaces at x = +L? (d) Obtain an expression for the heat flux distribution q (as a function of x). Is the heat flux zero at any location? (e) If the source of the heat generation is suddenly deactivated (i. e. q = 0), what temperature will the wall eventually reach with q = 0?arrow_forwardplease provide answers with step-by-step calculations and explanationarrow_forward
- Which formula is used to calculate the heat conduction in the AXIAL direction in a vertically located pipe segment whose inner and outer surfaces are perfectly insulated. Here r, is inner radius, r, outer radius, Tri pipe inner surface temperature, Tro pipe outer surface temperature, L is the length of the pipe, T the temperature on the lower surface, Ty the temperature on upper surface. Tu r; Tro rarrow_forward= Consider a large plane wall of thickness L=0.3 m, thermal conductivity k = 2.5 W/m.K, and surface area A = 12 m². The left side of the wall at x=0 is subjected to a net heat flux of ɖo = 700 W/m² while the temperature at that surface is measured to be T₁ = 80°C. Assuming constant thermal conductivity and no heat generation in the wall, (a) express the differential equation and the boundary equations for steady one- dimensional heat conduction through the wall, (b) obtain a relation for the variation of the temperature in the wall by solving the differential equation, and (c) evaluate the temperature of the right surface of the wall at x=L. Ti до L Xarrow_forwardSolve using the methodology : Known, Find, Schematic Diagram, Assumptions, Properties, Analysis and Comments.arrow_forward
- Find the two-dimensional temperature distribution T(x,y) and midplane temperature T(B/2,W/2) under steady state condition. The density, conductivity and specific heat of the material are p=(1200*32)kg/mº, k=400 W/m.K, and cp=2500 J/kg.K, respectively. A uniform heat flux 9" =1000 W/m² is applied to the upper surface. The right and left surfaces are also kept at 0°C. Bottom surface is insulated. 9" (W/m) T=0°C T=0°C W=(10*32)cm B=(30*32)cmarrow_forwardContinuous temperature distribution in a semi-permeable material with laser radiation on it, thickness L and with a heat conduction coefficient k, T(x)=-A/k.a^2.e^-ax+Bx+C It is given by equality. Here A, a, B and C are known constants. For this case, the radiation absorption in the material manifests itself in a uniform heat generation term in the form q (x). a) Obtain a relationship for the type that gives the conduction heat fluxes on the front and back surfaces. b) get a correlation for q(x) c) Obtain a relation that gives the radiation energy produced per unit surface area in the whole material.arrow_forwardFind the two-dimensional temperature distribution T(x,y) and midplane temperature T(B/2,W/2) under steady state condition. The density, conductivity and specific heat of the material are ρ =1200 kg/m 3, k=400 W/m.K, and cp=2500 J/kg.K, respectively. A uniform heat flux q =1000 W/m 2 is applied to the upper surface. The right and left surfaces are also kept at 0oC. Bottom surface is insulated.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Understanding Conduction and the Heat Equation; Author: The Efficient Engineer;https://www.youtube.com/watch?v=6jQsLAqrZGQ;License: Standard youtube license