
Introduction to Heat Transfer
6th Edition
ISBN: 9780470501962
Author: Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, Adrienne S. Lavine
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 2, Problem 2.11P
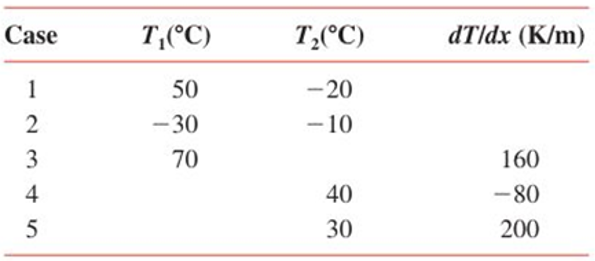
Consider steady-state conditions for one-dimensional conduction in a plane wall having a thermal conductivity

Determine the heat flux and the unknown quantity for each case and sketch the temperature distribution, indicating the direction of the heat flux.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Two large tanks, each holding 100 L of liquid, are interconnected by pipes, with the liquid flowing from tank
A into tank B at a rate of 3 L/min and from B into A at a rate of 1 L/min (see Figure Q1). The liquid inside each
tank is kept well stirred. A brine solution with a concentration of 0.2 kg/L of salt flows into tank A at a rate of
6 L/min. The diluted solution flows out of the system from tank A at 4 L/min and from tank B at 2 L/min. If,
initially, tank A contains pure water and tank B contains 20 kg of salt.
A
6 L/min
0.2 kg/L
x(t)
100 L
4 L/min
x(0) = 0 kg
3 L/min
1 L/min
B
y(t)
100 L
y(0) = 20 kg
2 L/min
Figure Q1 - Mixing problem for interconnected tanks
Determine the mass of salt in each tank at time t≥ 0:
Analytically (hand calculations)
Using MATLAB Numerical Functions (ode45)
Creating Simulink Model
Plot all solutions on the same graph for the first 15 min. The graph must be fully formatted by code.
5. Estimate the friction pressure gradient in a 10.15 cm bore unheated horizontal
pipe for the following conditions:
Fluid-propylene
Pressure 8.175 bar
Temperature-7°C
Mass flow of liquid-2.42 kg/s. Density of liquid-530 kg/m³
Mass flow of vapour-0.605 kg/s. Density of vapour-1.48 kg/m³
Describe the following HVAC systems.
a) All-air systems
b) All-water systems
c) Air-water systems
Graphically represent each system with a sketch.
Chapter 2 Solutions
Introduction to Heat Transfer
Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - Assume steady-state, one-dimensional conduction in...Ch. 2 - A hot water pipe with outside radius r1 has a...Ch. 2 - A spherical shell with inner radius r1 and outer...Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - A composite rod consists of two different...Ch. 2 - A solid, truncated cone serves as a support for a...Ch. 2 - To determine the effect of the temperature...Ch. 2 - Prob. 2.9PCh. 2 - A one-dimensional plane wall of thickness 2L=100mm...
Ch. 2 - Consider steady-state conditions for...Ch. 2 - Consider a plane wall 100 mm thick and of thermal...Ch. 2 - Prob. 2.13PCh. 2 - In the two-dimensional body illustrated, the...Ch. 2 - Consider the geometry of Problem 2.14 for the case...Ch. 2 - Steady-state, one-dimensional conduction occurs in...Ch. 2 - Prob. 2.17PCh. 2 - Prob. 2.18PCh. 2 - Consider a 300mm300mm window in an aircraft. For a...Ch. 2 - Prob. 2.20PCh. 2 - Use IHT to perform the following tasks. Graph the...Ch. 2 - Calculate the thermal conductivity of air,...Ch. 2 - A method for determining the thermal conductivity...Ch. 2 - Prob. 2.24PCh. 2 - Prob. 2.25PCh. 2 - At a given instant of time, the temperature...Ch. 2 - Prob. 2.27PCh. 2 - Uniform internal heat generation at q.=5107W/m3 is...Ch. 2 - Prob. 2.29PCh. 2 - The steady-state temperature distribution in a...Ch. 2 - The temperature distribution across a wall 0.3 m...Ch. 2 - Prob. 2.32PCh. 2 - Prob. 2.33PCh. 2 - Prob. 2.34PCh. 2 - Prob. 2.35PCh. 2 - Prob. 2.36PCh. 2 - Prob. 2.37PCh. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - Prob. 2.42PCh. 2 - Prob. 2.43PCh. 2 - Prob. 2.44PCh. 2 - Beginning with a differential control volume in...Ch. 2 - A steam pipe is wrapped with insulation of inner...Ch. 2 - Prob. 2.47PCh. 2 - Prob. 2.48PCh. 2 - Two-dimensional, steady-state conduction occurs in...Ch. 2 - Prob. 2.50PCh. 2 - Prob. 2.51PCh. 2 - A chemically reacting mixture is stored in a...Ch. 2 - A thin electrical heater dissipating 4000W/m2 is...Ch. 2 - The one-dimensional system of mass M with constant...Ch. 2 - Consider a one-dimensional plane wall of thickness...Ch. 2 - A large plate of thickness 2L is at a uniform...Ch. 2 - Prob. 2.57PCh. 2 - Prob. 2.58PCh. 2 - A plane wall has constant properties, no internal...Ch. 2 - A plane wall with constant properties is initially...Ch. 2 - Consider the conditions associated with Problem...Ch. 2 - Prob. 2.62PCh. 2 - A spherical particle of radius r1 experiences...Ch. 2 - Prob. 2.64PCh. 2 - A plane wall of thickness L=0.1m experiences...Ch. 2 - Prob. 2.66PCh. 2 - A composite one-dimensional plane wall is of...Ch. 2 - Prob. 2.68PCh. 2 - The steady-state temperature distribution in a...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Two large tanks, each holding 100 L of liquid, are interconnected by pipes, with the liquid flowing from tank A into tank B at a rate of 3 L/min and from B into A at a rate of 1 L/min (see Figure Q1). The liquid inside each tank is kept well stirred. A brine solution with a concentration of 0.2 kg/L of salt flows into tank A at a rate of 6 L/min. The diluted solution flows out of the system from tank A at 4 L/min and from tank B at 2 L/min. If, initially, tank A contains pure water and tank B contains 20 kg of salt. A 6 L/min 0.2 kg/L x(t) 100 L 4 L/min x(0) = 0 kg 3 L/min 1 L/min B y(t) 100 L y(0) = 20 kg 2 L/min Figure Q1 - Mixing problem for interconnected tanks Determine the mass of salt in each tank at time t≥ 0: Analytically (hand calculations) Using MATLAB Numerical Functions (ode45) Creating Simulink Model Plot all solutions on the same graph for the first 15 min. The graph must be fully formatted by code.arrow_forwardased on the corresponding mass flow rates (and NOT the original volumetric flow rates) determine: a) The mass flow rate of the mixed air (i.e., the combination of the two flows) leaving the chamber in kg/s. b) The temperature of the mixed air leaving the chamber. Please use PyscPro software for solving this question. Notes: For part (a), you will first need to find the density or specific volume for each state (density = 1/specific volume). The units the 'v' and 'a' are intended as subscripts: · kgv = kg_v = kgv = kilogram(s) [vapour] kga = kg_a =kga = kilogram(s) [air]arrow_forwardThe answers to this question s wasn't properly given, I need expert handwritten solutionsarrow_forward
- I need expert handwritten solutions to this onlyarrow_forwardTwo large tanks, each holding 100 L of liquid, are interconnected by pipes, with the liquid flowing from tank A into tank B at a rate of 3 L/min and from B into A at a rate of 1 L/min (see Figure Q1). The liquid inside each tank is kept well stirred. A brine solution with a concentration of 0.2 kg/L of salt flows into tank A at a rate of 6 L/min. The diluted solution flows out of the system from tank A at 4 L/min and from tank B at 2 L/min. If, initially, tank A contains pure water and tank B contains 20 kg of salt. A 6 L/min 0.2 kg/L x(t) 100 L 4 L/min x(0) = 0 kg 3 L/min B y(t) 100 L y(0) = 20 kg 2 L/min 1 L/min Figure Q1 - Mixing problem for interconnected tanks Determine the mass of salt in each tank at time t > 0: Analytically (hand calculations)arrow_forwardTwo springs and two masses are attached in a straight vertical line as shown in Figure Q3. The system is set in motion by holding the mass m₂ at its equilibrium position and pushing the mass m₁ downwards of its equilibrium position a distance 2 m and then releasing both masses. if m₁ = m₂ = 1 kg, k₁ = 3 N/m and k₂ = 2 N/m. www.m k₁ = 3 (y₁ = 0). m₁ = 1 k2=2 (y₂ = 0) |m₂ = 1 Y2 y 2 System in static equilibrium (Net change in spring length =32-31) System in motion Figure Q3 - Coupled mass-spring system Determine the equations of motion y₁(t) and y₂(t) for the two masses m₁ and m₂ respectively: Analytically (hand calculations)arrow_forward
- 100 As a spring is heated, its spring constant decreases. Suppose the spring is heated and then cooled so that the spring constant at time t is k(t) = t sin N/m. If the mass-spring system has mass m = 2 kg and a damping constant b = 1 N-sec/m with initial conditions x(0) = 6 m and x'(0) = -5 m/sec and it is subjected to the harmonic external force f(t) = 100 cos 3t N. Find at least the first four nonzero terms in a power series expansion about t = 0, i.e. Maclaurin series expansion, for the displacement: Analytically (hand calculations)arrow_forwardthis is answer to a vibrations question. in the last part it states an assumption of x2, im not sure where this assumption comes from. an answer would be greatly appreciatedarrow_forwardPlease answer with the sketches.arrow_forward
- The beam is made of elastic perfectly plastic material. Determine the shape factor for the cross section of the beam (Figure Q3). [Take σy = 250 MPa, yNA = 110.94 mm, I = 78.08 x 106 mm²] y 25 mm 75 mm I 25 mm 200 mm 25 mm 125 Figure Q3arrow_forwardA beam of the cross section shown in Figure Q3 is made of a steel that is assumed to be elastic- perfectectly plastic material with E = 200 GPa and σy = 240 MPa. Determine: i. The shape factor of the cross section ii. The bending moment at which the plastic zones at the top and bottom of the bar are 30 mm thick. 15 mm 30 mm 15 mm 30 mm 30 mm 30 mmarrow_forwardA torque of magnitude T = 12 kNm is applied to the end of a tank containing compressed air under a pressure of 8 MPa (Figure Q1). The tank has a 180 mm inner diameter and a 12 mm wall thickness. As a result of several tensile tests, it has been found that tensile yeild strength is σy = 250 MPa for thr grade of steel used. Determine the factor of safety with respect to yeild, using: (a) The maximum shearing stress theory (b) The maximum distortion energy theory T Figure Q1arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning

Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Understanding Conduction and the Heat Equation; Author: The Efficient Engineer;https://www.youtube.com/watch?v=6jQsLAqrZGQ;License: Standard youtube license