Introduction to Heat Transfer
6th Edition
ISBN: 9780470501962
Author: Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, Adrienne S. Lavine
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2, Problem 2.2P
Assume steady-state, one-dimensional conduction in the axisymmetric object below, which is insulated around its perimeter.
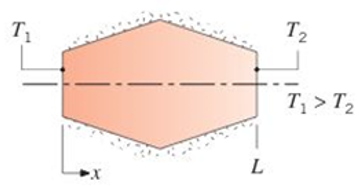
If the properties remain constant and no internal heat generation occurs, sketch the heat flux distribution,
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
2. A rectangular block has thickness B in the x-direction. The side at x = 0 is held at temperature
T, while the side at x = B is held at T2. The other four sides are well insulated. Heat is generated
in the block at a uniform rate per unit volume of [.
(a) Use the conduction equation to derive an expression for the steady-state temperature profile,
T(x). Assume constant thermal conductivity.
(b) Use the result of part (a) to calculate the maximum temperature in the block for the following
values of the parameters:
T₁-120 °C k-0.2 W/(m K) B-1.0 m T₂-0 F-100 W/m³
Do part 3,4
Please help me answer question 1, show all the steps taken.
Chapter 2 Solutions
Introduction to Heat Transfer
Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - Assume steady-state, one-dimensional conduction in...Ch. 2 - A hot water pipe with outside radius r1 has a...Ch. 2 - A spherical shell with inner radius r1 and outer...Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - A composite rod consists of two different...Ch. 2 - A solid, truncated cone serves as a support for a...Ch. 2 - To determine the effect of the temperature...Ch. 2 - Prob. 2.9PCh. 2 - A one-dimensional plane wall of thickness 2L=100mm...
Ch. 2 - Consider steady-state conditions for...Ch. 2 - Consider a plane wall 100 mm thick and of thermal...Ch. 2 - Prob. 2.13PCh. 2 - In the two-dimensional body illustrated, the...Ch. 2 - Consider the geometry of Problem 2.14 for the case...Ch. 2 - Steady-state, one-dimensional conduction occurs in...Ch. 2 - Prob. 2.17PCh. 2 - Prob. 2.18PCh. 2 - Consider a 300mm300mm window in an aircraft. For a...Ch. 2 - Prob. 2.20PCh. 2 - Use IHT to perform the following tasks. Graph the...Ch. 2 - Calculate the thermal conductivity of air,...Ch. 2 - A method for determining the thermal conductivity...Ch. 2 - Prob. 2.24PCh. 2 - Prob. 2.25PCh. 2 - At a given instant of time, the temperature...Ch. 2 - Prob. 2.27PCh. 2 - Uniform internal heat generation at q.=5107W/m3 is...Ch. 2 - Prob. 2.29PCh. 2 - The steady-state temperature distribution in a...Ch. 2 - The temperature distribution across a wall 0.3 m...Ch. 2 - Prob. 2.32PCh. 2 - Prob. 2.33PCh. 2 - Prob. 2.34PCh. 2 - Prob. 2.35PCh. 2 - Prob. 2.36PCh. 2 - Prob. 2.37PCh. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - Prob. 2.42PCh. 2 - Prob. 2.43PCh. 2 - Prob. 2.44PCh. 2 - Beginning with a differential control volume in...Ch. 2 - A steam pipe is wrapped with insulation of inner...Ch. 2 - Prob. 2.47PCh. 2 - Prob. 2.48PCh. 2 - Two-dimensional, steady-state conduction occurs in...Ch. 2 - Prob. 2.50PCh. 2 - Prob. 2.51PCh. 2 - A chemically reacting mixture is stored in a...Ch. 2 - A thin electrical heater dissipating 4000W/m2 is...Ch. 2 - The one-dimensional system of mass M with constant...Ch. 2 - Consider a one-dimensional plane wall of thickness...Ch. 2 - A large plate of thickness 2L is at a uniform...Ch. 2 - Prob. 2.57PCh. 2 - Prob. 2.58PCh. 2 - A plane wall has constant properties, no internal...Ch. 2 - A plane wall with constant properties is initially...Ch. 2 - Consider the conditions associated with Problem...Ch. 2 - Prob. 2.62PCh. 2 - A spherical particle of radius r1 experiences...Ch. 2 - Prob. 2.64PCh. 2 - A plane wall of thickness L=0.1m experiences...Ch. 2 - Prob. 2.66PCh. 2 - A composite one-dimensional plane wall is of...Ch. 2 - Prob. 2.68PCh. 2 - The steady-state temperature distribution in a...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Can you help me with question 3 show all the steps taken.arrow_forward8m long rod is at an initial temperature of 80c the left side of the rod is at temperature equal to 39c and the right side is at temperature equal to 68c thermal diffusivity is equal to 10^-4 and grid space is equal to 2m find the temperature distribution at 30_60_90 secondsarrow_forwardHi, kindly help me with this and show the complete solution. Thank youarrow_forward
- 4arrow_forwardThe thermal conductivity of a specific material is highly dependent on a number of factors. These include the temperature gradient, the properties of the material, and the path length that the heat follows. My question is how to add thermal conductivity? for example SS316 material has thermal conductivity=15W/mk if Gyroid shape is created with SS316 then what will be the total thermal conductivity?arrow_forwardLooking for a handwritten solution as fast as possible.arrow_forward
- : Assume steady-state, one-dimensional heat conduction through the symmetric shape shown in Figure 1. Assuming that there is no internal heat generation, derive an expression for the thermal conductivity k(x) for these conditions: A(x) = (1 - x), T(x) = 300(1 - 2x - x3), and q = 6000 W, where A is in square meters, T in kelvins, and x in meters. Consider x= 0 and 1.arrow_forwardQuestion 5:Assume steady-state, one-dimensional heat conduction through the symmetric shape shown in Figure 1.Assuming that there is no internal heat generation, derive an expression for the thermal conductivity k(x) for these conditions: A(x) = (1 -x), T(x) = 300(1 - 2x -x3),and q = 6000 W, where A is in square meters, T in kelvins, and x in meters. Consider x= 0 and 1arrow_forwardHi, kindly solve this problem and show the solution. Thank youarrow_forward
- A square piece is initially at 10 degrees Celsius everywhere. Each side is 0.05 m long. Then the four sides are instantly heated up to 25 degrees Celsius, 50 degrees Celsius, 30 degrees Celsius, and 0 degrees Celsius. a. Find how long it takes for the temperature profile of this square to become steady if the material is copper. What is the final temperature at the center of the square? b. Find how long it takes for the temperature profile of this square to become steady if the material is air. What is the final temperature at the center of the square? c. Which material takes longer to reach steady state and why?arrow_forward2. One end of a 40 cm metal rod 2.0 cm2 in cross section is in a steam bath while the other end is embedded in ice. It is observed that 13.3 grams of ice melted in 15 minutes from the heat conducted by the rod. What is the thermal conductivity of the rod.arrow_forwardA 20 cm thick block of copper is placed against a 40 cm block of iron. Let Question 9 the dimensions of the faces of each block be 3 m by 2 m. Also, the conductivity of copper is 200 and the conductivity of iron is 300 K. If the left face of the copper block is 100°C and the right face of the iron block is at 10°C, calculate: m K (a) the temperature between the blocks (the interface). (b) the heat transfer rate through the system of blocks. Question 10 Its separates the inside of your home, which is at 30°C, from the outside, which is at 5°C. If the conductivity of the window is 250, calculate the heat transfer rate through There is a window whose dimensions are 2 m by 3 m, and is 10 cm thick. the window.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Understanding Conduction and the Heat Equation; Author: The Efficient Engineer;https://www.youtube.com/watch?v=6jQsLAqrZGQ;License: Standard youtube license