Chapter 2, Problem 132CR

To determine

To graph: the function $f(x)$ and check for intercept and various asymptotes.

Answer to Problem 132CR

y-intercept is $0$

x-intercept is $0$

Vertical asymptote is at $x=\pm 2$

Horizontal asymptote is at $y=2$

No holes

No slant asymptotes

Explanation of Solution

Given information:

  $f(x)=\frac{2x^2}{x^2-4}$

Graph: Assuming the value of x to find $f(x)$ and plot the graph

  

  

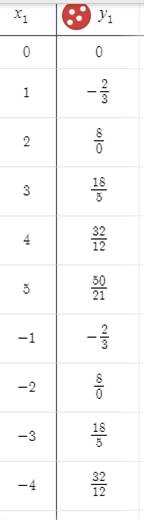
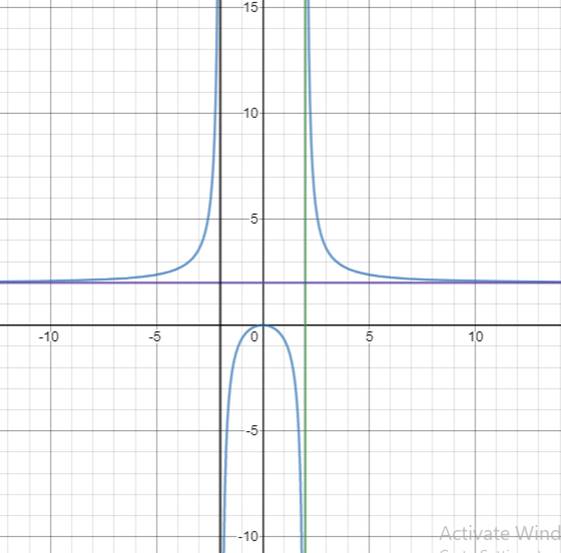
Interpretation :

To determine y-intercept put $x=0$ and solve for $y$ or $f(x)$

  $f(x)=\frac{2x^2}{x^2-4}=\frac{2\times 0^2}{0^2-4}=0$

To determine x-intercept put $y=0$ and solve for $x$

  $f(x)=\frac{2x^2}{x^2-4}\Rightarrow 0=\frac{2x^2}{x^2-4}\Rightarrow 2x^2=0\Rightarrow x=0$

To find the vertical asymptotes we have to solve the denominator by equating it equal to zero:

  $x^2-4=0\Rightarrow x^2=4\Rightarrow x=\pm 2$

A horizontal asymptotes is defined when the degree of the denominator is greater than or equal to degree of the numerator.

Here the degree of denominator is equal to numerator therefore we calculate $\underset{x\to \infty }{\lim }f(x)$

  $\begin{array}{c}\underset{x\to \infty }{\lim }f(x)=\underset{x\to \infty }{\lim }\frac{2x^2}{x^2-4}\\ =\underset{x\to \infty }{\lim }\frac{\frac{2x^2}{x^2}}{{\frac{x}{x^2}}^2-\frac{4}{2x^2}}\\ =\underset{x\to \infty }{\lim }\frac{2}{1-\frac{2}{x^2}}\\ =\underset{x\to \infty }{\lim }\frac{2}{1-\frac{2}{\infty }}\\ =\underset{x\to \infty }{\lim }\frac{2}{1-0}\\ =2\end{array}$

As $x$ gets bigger $f(x)$ gets nearer to zero

Therefore after solving horizontal asymptote is at $y=2$

Slant asymptotes occur when the degree of denominator is lower than that of the numerator. since the function is having horizontal asymptotes therefore slant asymptote is not possible.

Now, the degree of the denominator is equal to the degree of the numerator therefore there will be a hole possible in the graph.

But in the given function there is no common factor found both at numerator and denominator

Therefore there is no hole for the given function.