EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR
8th Edition
ISBN: 9780357022078
Author: Larson
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 2.2, Problem 118E
(a)
To determine
The degree of the polynomial function that represents the graph.
(a)
Expert Solution
Answer to Problem 118E
The degree of the polynomial is 3.
Explanation of Solution
Given information:
The graph is shown below as,
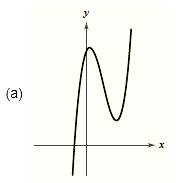
Formula used:
The leading coefficient is used.
Calculation:
Consider the following graph
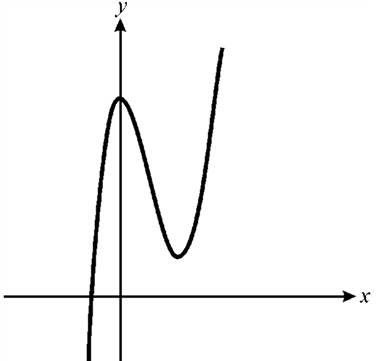
Since the graph rises to right and falls to the left, hence the leading coefficient is negative and degree of the polynomial is odd.
From the above it is clear that the graph has only one root. Since the graph crosses the x-axis, hence this root has odd multiplicity.
Also the graph has two turns; hence the degree of the polynomial is 3.
Conclusion:
The degree of the polynomial is 3.
(b)
To determine
To find: The degree of the polynomial function that represents the graph.
(b)
Expert Solution
Answer to Problem 118E
The degree of the polynomial is 2.
Explanation of Solution
Given information:
The graph is given as,
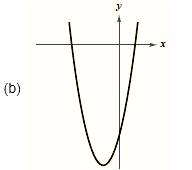
Formula used:
The leading coefficient is used.
Calculation:
Since the graph rises to right and to the left, hence the leading coefficient is positive and degree of the polynomial is even.
From the above it is clear that the graph has two roots. Since the graph crosses the x-axis, hence these roots have odd multiplicity.
Also the graph has one turn; hence the degree of the polynomial is 2.
Conclusion:
The degree of the polynomial is 2.
(c)
To determine
To find: The degree of the polynomial function that represents the graph.
(c)
Expert Solution
Answer to Problem 118E
The degree of the polynomial is 4.
Explanation of Solution
Given information:
The graph is given as,
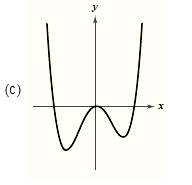
Formula used:
The leading coefficient is used.
Calculation:
Consider the following graph
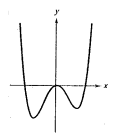
Since the graph rises to right and to the left, hence the leading coefficient is positive and degree of the polynomial is even.
From the above it is clear that the graph has three roots. Since the graph crosses the x-axis at two points, hence these roots have odd multiplicity. The graph touches the x-axis at one point hence this root has even multiplicity.
Also the graph has three turns; hence the degree of the polynomial is 4.
Conclusion:
The degree of the polynomial is 4.
(d)
To determine
To find: The degree of the polynomial function that represents the graph.
(d)
Expert Solution
Answer to Problem 118E
The degree of the polynomial is 5.
Explanation of Solution
Given information:
The graph is given as,
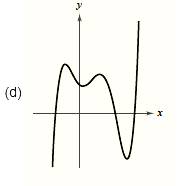
Formula used:
The leading coefficient is used.
Calculation:
Consider the following graph
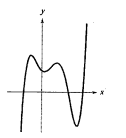
Since the graph rises to right and falls to the left, hence the leading coefficient is negative and degree of the polynomial is odd.
From the above it is clear that the graph has three roots. Since the graph crosses the x-axis at three points, hence these roots have odd multiplicity. Also the graph has four turns; hence the degree of the polynomial is 5.
Conclusion:
The degree of the polynomial is 5.
Chapter 2 Solutions
EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR
Ch. 2.1 - Prob. 1ECh. 2.1 - Prob. 2ECh. 2.1 - Prob. 3ECh. 2.1 - Prob. 4ECh. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - Prob. 9ECh. 2.1 - Prob. 10E
Ch. 2.1 - Prob. 11ECh. 2.1 - Prob. 12ECh. 2.1 - Prob. 13ECh. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - Prob. 25ECh. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Prob. 32ECh. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.1 - Prob. 41ECh. 2.1 - Prob. 42ECh. 2.1 - Prob. 43ECh. 2.1 - Prob. 44ECh. 2.1 - Prob. 45ECh. 2.1 - Prob. 46ECh. 2.1 - Prob. 47ECh. 2.1 - Prob. 48ECh. 2.1 - Prob. 49ECh. 2.1 - Prob. 50ECh. 2.1 - Prob. 51ECh. 2.1 - Prob. 52ECh. 2.1 - Prob. 53ECh. 2.1 - Prob. 54ECh. 2.1 - Prob. 55ECh. 2.1 - Prob. 56ECh. 2.1 - Prob. 57ECh. 2.1 - Prob. 58ECh. 2.1 - Prob. 59ECh. 2.1 - Prob. 60ECh. 2.1 - Prob. 61ECh. 2.1 - Prob. 62ECh. 2.1 - Prob. 63ECh. 2.1 - Prob. 64ECh. 2.1 - Prob. 65ECh. 2.1 - Prob. 66ECh. 2.1 - Prob. 67ECh. 2.1 - Prob. 68ECh. 2.1 - Prob. 69ECh. 2.1 - Prob. 70ECh. 2.1 - Prob. 71ECh. 2.1 - Prob. 72ECh. 2.1 - Prob. 73ECh. 2.1 - Prob. 74ECh. 2.1 - Prob. 75ECh. 2.1 - Prob. 76ECh. 2.1 - Prob. 77ECh. 2.1 - Prob. 78ECh. 2.1 - Prob. 79ECh. 2.1 - Prob. 80ECh. 2.1 - Prob. 81ECh. 2.1 - Prob. 82ECh. 2.1 - Prob. 83ECh. 2.1 - Prob. 84ECh. 2.1 - Prob. 85ECh. 2.1 - Prob. 86ECh. 2.1 - Prob. 87ECh. 2.1 - Prob. 88ECh. 2.1 - Prob. 89ECh. 2.2 - Prob. 1ECh. 2.2 - Prob. 2ECh. 2.2 - Prob. 3ECh. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Prob. 11ECh. 2.2 - Prob. 12ECh. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Prob. 48ECh. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - Prob. 51ECh. 2.2 - Prob. 52ECh. 2.2 - Prob. 53ECh. 2.2 - Prob. 54ECh. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - Prob. 57ECh. 2.2 - Prob. 58ECh. 2.2 - Prob. 59ECh. 2.2 - Prob. 60ECh. 2.2 - Prob. 61ECh. 2.2 - Prob. 62ECh. 2.2 - Prob. 63ECh. 2.2 - Prob. 64ECh. 2.2 - Prob. 65ECh. 2.2 - Prob. 66ECh. 2.2 - Prob. 67ECh. 2.2 - Prob. 68ECh. 2.2 - Prob. 69ECh. 2.2 - Prob. 70ECh. 2.2 - Prob. 71ECh. 2.2 - Prob. 72ECh. 2.2 - Prob. 73ECh. 2.2 - Prob. 74ECh. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2.2 - Prob. 77ECh. 2.2 - Prob. 78ECh. 2.2 - Prob. 79ECh. 2.2 - Prob. 80ECh. 2.2 - Prob. 81ECh. 2.2 - Prob. 82ECh. 2.2 - Prob. 83ECh. 2.2 - Prob. 84ECh. 2.2 - Prob. 85ECh. 2.2 - Prob. 86ECh. 2.2 - Prob. 87ECh. 2.2 - Prob. 88ECh. 2.2 - Prob. 89ECh. 2.2 - Prob. 90ECh. 2.2 - Prob. 91ECh. 2.2 - Prob. 92ECh. 2.2 - Prob. 93ECh. 2.2 - Prob. 94ECh. 2.2 - Prob. 95ECh. 2.2 - Prob. 96ECh. 2.2 - Prob. 97ECh. 2.2 - Prob. 98ECh. 2.2 - Prob. 99ECh. 2.2 - Prob. 100ECh. 2.2 - Prob. 101ECh. 2.2 - Prob. 102ECh. 2.2 - Prob. 103ECh. 2.2 - Prob. 104ECh. 2.2 - Prob. 105ECh. 2.2 - Prob. 106ECh. 2.2 - Prob. 107ECh. 2.2 - Prob. 108ECh. 2.2 - Prob. 109ECh. 2.2 - Prob. 110ECh. 2.2 - Prob. 111ECh. 2.2 - Prob. 112ECh. 2.2 - Prob. 113ECh. 2.2 - Prob. 114ECh. 2.2 - Prob. 115ECh. 2.2 - Prob. 116ECh. 2.2 - Prob. 117ECh. 2.2 - Prob. 118ECh. 2.2 - Prob. 119ECh. 2.2 - Prob. 120ECh. 2.2 - Prob. 121ECh. 2.2 - Prob. 122ECh. 2.2 - Prob. 123ECh. 2.2 - Prob. 124ECh. 2.2 - Prob. 125ECh. 2.2 - Prob. 126ECh. 2.2 - Prob. 127ECh. 2.2 - Prob. 128ECh. 2.3 - Prob. 1ECh. 2.3 - Prob. 2ECh. 2.3 - Prob. 3ECh. 2.3 - Prob. 4ECh. 2.3 - Prob. 5ECh. 2.3 - Prob. 6ECh. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - Prob. 21ECh. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Prob. 38ECh. 2.3 - Prob. 39ECh. 2.3 - Prob. 40ECh. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - Prob. 43ECh. 2.3 - Prob. 44ECh. 2.3 - Prob. 45ECh. 2.3 - Prob. 46ECh. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Prob. 49ECh. 2.3 - Prob. 50ECh. 2.3 - Prob. 51ECh. 2.3 - Prob. 52ECh. 2.3 - Prob. 53ECh. 2.3 - Prob. 54ECh. 2.3 - Prob. 55ECh. 2.3 - Prob. 56ECh. 2.3 - Prob. 57ECh. 2.3 - Prob. 58ECh. 2.3 - Prob. 59ECh. 2.3 - Prob. 60ECh. 2.3 - Prob. 61ECh. 2.3 - Prob. 62ECh. 2.3 - Prob. 63ECh. 2.3 - Prob. 64ECh. 2.3 - Prob. 65ECh. 2.3 - Prob. 66ECh. 2.3 - Prob. 67ECh. 2.3 - Prob. 68ECh. 2.3 - Prob. 69ECh. 2.3 - Prob. 70ECh. 2.3 - Prob. 71ECh. 2.3 - Prob. 72ECh. 2.3 - Prob. 73ECh. 2.3 - Prob. 74ECh. 2.3 - Prob. 75ECh. 2.3 - Prob. 76ECh. 2.3 - Prob. 77ECh. 2.3 - Prob. 78ECh. 2.3 - Prob. 79ECh. 2.3 - Prob. 80ECh. 2.3 - Prob. 81ECh. 2.3 - Prob. 82ECh. 2.3 - Prob. 83ECh. 2.3 - Prob. 84ECh. 2.3 - Prob. 85ECh. 2.3 - Prob. 86ECh. 2.3 - Prob. 87ECh. 2.3 - Prob. 88ECh. 2.3 - Prob. 89ECh. 2.3 - Prob. 90ECh. 2.3 - Prob. 91ECh. 2.3 - Prob. 92ECh. 2.3 - Prob. 93ECh. 2.3 - Prob. 94ECh. 2.3 - Prob. 95ECh. 2.3 - Prob. 96ECh. 2.3 - Prob. 97ECh. 2.3 - Prob. 98ECh. 2.3 - Prob. 99ECh. 2.3 - Prob. 100ECh. 2.3 - Prob. 101ECh. 2.3 - Prob. 102ECh. 2.3 - Prob. 103ECh. 2.3 - Prob. 104ECh. 2.3 - Prob. 105ECh. 2.3 - Prob. 106ECh. 2.3 - Prob. 107ECh. 2.3 - Prob. 108ECh. 2.3 - Prob. 109ECh. 2.3 - Prob. 110ECh. 2.3 - Prob. 111ECh. 2.3 - Prob. 112ECh. 2.3 - Prob. 113ECh. 2.3 - Prob. 114ECh. 2.3 - Prob. 115ECh. 2.3 - Prob. 116ECh. 2.3 - Prob. 117ECh. 2.3 - Prob. 118ECh. 2.3 - Prob. 119ECh. 2.3 - Prob. 120ECh. 2.4 - Prob. 1ECh. 2.4 - Prob. 2ECh. 2.4 - Prob. 3ECh. 2.4 - Prob. 4ECh. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - Prob. 12ECh. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - Prob. 18ECh. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Prob. 23ECh. 2.4 - Prob. 24ECh. 2.4 - Prob. 25ECh. 2.4 - Prob. 26ECh. 2.4 - Prob. 27ECh. 2.4 - Prob. 28ECh. 2.4 - Prob. 29ECh. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Prob. 33ECh. 2.4 - Prob. 34ECh. 2.4 - Prob. 35ECh. 2.4 - Prob. 36ECh. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Prob. 39ECh. 2.4 - Prob. 40ECh. 2.4 - Prob. 41ECh. 2.4 - Prob. 42ECh. 2.4 - Prob. 43ECh. 2.4 - Prob. 44ECh. 2.4 - Prob. 45ECh. 2.4 - Prob. 46ECh. 2.4 - Prob. 47ECh. 2.4 - Prob. 48ECh. 2.4 - Prob. 49ECh. 2.4 - Prob. 50ECh. 2.4 - Prob. 51ECh. 2.4 - Prob. 52ECh. 2.4 - Prob. 53ECh. 2.4 - Prob. 54ECh. 2.4 - Prob. 55ECh. 2.4 - Prob. 56ECh. 2.4 - Prob. 57ECh. 2.4 - Prob. 58ECh. 2.4 - Prob. 59ECh. 2.4 - Prob. 60ECh. 2.4 - Prob. 61ECh. 2.4 - Prob. 62ECh. 2.4 - Prob. 63ECh. 2.4 - Prob. 64ECh. 2.4 - Prob. 65ECh. 2.4 - Prob. 66ECh. 2.4 - Prob. 67ECh. 2.4 - Prob. 68ECh. 2.4 - Prob. 69ECh. 2.4 - Prob. 70ECh. 2.4 - Prob. 71ECh. 2.4 - Prob. 72ECh. 2.4 - Prob. 73ECh. 2.4 - Prob. 74ECh. 2.4 - Prob. 75ECh. 2.4 - Prob. 76ECh. 2.4 - Prob. 77ECh. 2.4 - Prob. 78ECh. 2.4 - Prob. 79ECh. 2.4 - Prob. 80ECh. 2.4 - Prob. 81ECh. 2.4 - Prob. 82ECh. 2.4 - Prob. 83ECh. 2.4 - Prob. 84ECh. 2.4 - Prob. 85ECh. 2.4 - Prob. 86ECh. 2.4 - Prob. 87ECh. 2.4 - Prob. 88ECh. 2.4 - Prob. 89ECh. 2.4 - Prob. 90ECh. 2.4 - Prob. 91ECh. 2.4 - Prob. 92ECh. 2.4 - Prob. 93ECh. 2.4 - Prob. 94ECh. 2.4 - Prob. 95ECh. 2.4 - Prob. 96ECh. 2.4 - Prob. 97ECh. 2.4 - Prob. 98ECh. 2.5 - Prob. 1ECh. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - Prob. 9ECh. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Prob. 37ECh. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - Prob. 40ECh. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - Prob. 45ECh. 2.5 - Prob. 46ECh. 2.5 - Prob. 47ECh. 2.5 - Prob. 48ECh. 2.5 - Prob. 49ECh. 2.5 - Prob. 50ECh. 2.5 - Prob. 51ECh. 2.5 - Prob. 52ECh. 2.5 - Prob. 53ECh. 2.5 - Prob. 54ECh. 2.5 - Prob. 55ECh. 2.5 - Prob. 56ECh. 2.5 - Prob. 57ECh. 2.5 - Prob. 58ECh. 2.5 - Prob. 59ECh. 2.5 - Prob. 60ECh. 2.5 - Prob. 61ECh. 2.5 - Prob. 62ECh. 2.5 - Prob. 63ECh. 2.5 - Prob. 64ECh. 2.5 - Prob. 65ECh. 2.5 - Prob. 66ECh. 2.5 - Prob. 67ECh. 2.5 - Prob. 68ECh. 2.5 - Prob. 69ECh. 2.5 - Prob. 70ECh. 2.5 - Prob. 71ECh. 2.5 - Prob. 72ECh. 2.5 - Prob. 73ECh. 2.5 - Prob. 74ECh. 2.5 - Prob. 75ECh. 2.5 - Prob. 76ECh. 2.5 - Prob. 77ECh. 2.5 - Prob. 78ECh. 2.6 - Prob. 1ECh. 2.6 - Prob. 2ECh. 2.6 - Prob. 3ECh. 2.6 - Prob. 4ECh. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Prob. 12ECh. 2.6 - Prob. 13ECh. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Prob. 16ECh. 2.6 - Prob. 17ECh. 2.6 - Prob. 18ECh. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - Prob. 21ECh. 2.6 - Prob. 22ECh. 2.6 - Prob. 23ECh. 2.6 - Prob. 24ECh. 2.6 - Prob. 25ECh. 2.6 - Prob. 26ECh. 2.6 - Prob. 27ECh. 2.6 - Prob. 28ECh. 2.6 - Prob. 29ECh. 2.6 - Prob. 30ECh. 2.6 - Prob. 31ECh. 2.6 - Prob. 32ECh. 2.6 - Prob. 33ECh. 2.6 - Prob. 34ECh. 2.6 - Prob. 35ECh. 2.6 - Prob. 36ECh. 2.6 - Prob. 37ECh. 2.6 - Prob. 38ECh. 2.6 - Prob. 39ECh. 2.6 - Prob. 40ECh. 2.6 - Prob. 41ECh. 2.6 - Prob. 42ECh. 2.6 - Prob. 43ECh. 2.6 - Prob. 44ECh. 2.6 - Prob. 45ECh. 2.6 - Prob. 46ECh. 2.6 - Prob. 47ECh. 2.6 - Prob. 48ECh. 2.6 - Prob. 49ECh. 2.6 - Prob. 50ECh. 2.6 - Prob. 51ECh. 2.6 - Prob. 52ECh. 2.6 - Prob. 53ECh. 2.6 - Prob. 54ECh. 2.6 - Prob. 55ECh. 2.6 - Prob. 56ECh. 2.6 - Prob. 57ECh. 2.6 - Prob. 58ECh. 2.6 - Prob. 59ECh. 2.6 - Prob. 60ECh. 2.6 - Prob. 61ECh. 2.6 - Prob. 62ECh. 2.6 - Prob. 63ECh. 2.6 - Prob. 64ECh. 2.6 - Prob. 65ECh. 2.6 - Prob. 66ECh. 2.7 - Prob. 1ECh. 2.7 - Prob. 2ECh. 2.7 - Prob. 3ECh. 2.7 - Prob. 4ECh. 2.7 - Prob. 5ECh. 2.7 - Prob. 6ECh. 2.7 - Prob. 7ECh. 2.7 - Prob. 8ECh. 2.7 - Prob. 9ECh. 2.7 - Prob. 10ECh. 2.7 - Prob. 11ECh. 2.7 - Prob. 12ECh. 2.7 - Prob. 13ECh. 2.7 - Prob. 14ECh. 2.7 - Prob. 15ECh. 2.7 - Prob. 16ECh. 2.7 - Prob. 17ECh. 2.7 - Prob. 18ECh. 2.7 - Prob. 19ECh. 2.7 - Prob. 20ECh. 2.7 - Prob. 21ECh. 2.7 - Prob. 22ECh. 2.7 - Prob. 23ECh. 2.7 - Prob. 24ECh. 2.7 - Prob. 25ECh. 2.7 - Prob. 26ECh. 2.7 - Prob. 27ECh. 2.7 - Prob. 28ECh. 2.7 - Prob. 29ECh. 2.7 - Prob. 30ECh. 2.7 - Prob. 31ECh. 2.7 - Prob. 32ECh. 2.7 - Prob. 33ECh. 2.7 - Prob. 34ECh. 2.7 - Prob. 35ECh. 2.7 - Prob. 36ECh. 2.7 - Prob. 37ECh. 2.7 - Prob. 38ECh. 2.7 - Prob. 39ECh. 2.7 - Prob. 40ECh. 2.7 - Prob. 41ECh. 2.7 - Prob. 42ECh. 2.7 - Prob. 43ECh. 2.7 - Prob. 44ECh. 2.7 - Prob. 45ECh. 2.7 - Prob. 46ECh. 2.7 - Prob. 47ECh. 2.7 - Prob. 48ECh. 2.7 - Prob. 49ECh. 2.7 - Prob. 50ECh. 2.7 - Prob. 51ECh. 2.7 - Prob. 52ECh. 2.7 - Prob. 53ECh. 2.7 - Prob. 54ECh. 2.7 - Prob. 55ECh. 2.7 - Prob. 56ECh. 2.7 - Prob. 57ECh. 2.7 - Prob. 58ECh. 2.7 - Prob. 59ECh. 2.7 - Prob. 60ECh. 2.7 - Prob. 61ECh. 2.7 - Prob. 62ECh. 2.7 - Prob. 63ECh. 2.7 - Prob. 64ECh. 2.7 - Prob. 65ECh. 2.7 - Prob. 66ECh. 2.7 - Prob. 67ECh. 2.7 - Prob. 68ECh. 2.7 - Prob. 69ECh. 2.7 - Prob. 70ECh. 2.7 - Prob. 71ECh. 2.7 - Prob. 72ECh. 2.7 - Prob. 73ECh. 2.7 - Prob. 74ECh. 2.7 - Prob. 75ECh. 2.7 - Prob. 76ECh. 2.7 - Prob. 77ECh. 2.7 - Prob. 78ECh. 2.7 - Prob. 79ECh. 2.7 - Prob. 80ECh. 2.7 - Prob. 81ECh. 2.7 - Prob. 82ECh. 2.7 - Prob. 83ECh. 2.7 - Prob. 84ECh. 2.7 - Prob. 85ECh. 2.7 - Prob. 86ECh. 2.7 - Prob. 87ECh. 2.7 - Prob. 88ECh. 2.7 - Prob. 89ECh. 2.7 - Prob. 90ECh. 2.7 - Prob. 91ECh. 2.7 - Prob. 92ECh. 2.7 - Prob. 93ECh. 2.7 - Prob. 94ECh. 2.7 - Prob. 95ECh. 2.7 - Prob. 96ECh. 2.7 - Prob. 97ECh. 2.7 - Prob. 98ECh. 2.7 - Prob. 99ECh. 2.7 - Prob. 100ECh. 2.7 - Prob. 101ECh. 2.8 - Prob. 1ECh. 2.8 - Prob. 2ECh. 2.8 - Prob. 3ECh. 2.8 - Prob. 4ECh. 2.8 - Prob. 5ECh. 2.8 - Prob. 6ECh. 2.8 - Prob. 7ECh. 2.8 - Prob. 8ECh. 2.8 - Prob. 9ECh. 2.8 - Prob. 10ECh. 2.8 - Prob. 11ECh. 2.8 - Prob. 12ECh. 2.8 - Prob. 13ECh. 2.8 - Prob. 14ECh. 2.8 - Prob. 15ECh. 2.8 - Prob. 16ECh. 2.8 - Prob. 17ECh. 2.8 - Prob. 18ECh. 2.8 - Prob. 19ECh. 2.8 - Prob. 20ECh. 2.8 - Prob. 21ECh. 2.8 - Prob. 22ECh. 2.8 - Prob. 23ECh. 2.8 - Prob. 24ECh. 2.8 - Prob. 25ECh. 2.8 - Prob. 26ECh. 2.8 - Prob. 27ECh. 2.8 - Prob. 28ECh. 2.8 - Prob. 29ECh. 2.8 - Prob. 30ECh. 2.8 - Prob. 31ECh. 2.8 - Prob. 32ECh. 2.8 - Prob. 33ECh. 2.8 - Prob. 34ECh. 2.8 - Prob. 35ECh. 2.8 - Prob. 36ECh. 2.8 - Prob. 37ECh. 2.8 - Prob. 38ECh. 2.8 - Prob. 39ECh. 2.8 - Prob. 40ECh. 2 - Prob. 1CRCh. 2 - Prob. 2CRCh. 2 - Prob. 3CRCh. 2 - Prob. 4CRCh. 2 - Prob. 5CRCh. 2 - Prob. 6CRCh. 2 - Prob. 7CRCh. 2 - Prob. 8CRCh. 2 - Prob. 9CRCh. 2 - Prob. 10CRCh. 2 - Prob. 11CRCh. 2 - Prob. 12CRCh. 2 - Prob. 13CRCh. 2 - Prob. 14CRCh. 2 - Prob. 15CRCh. 2 - Prob. 16CRCh. 2 - Prob. 17CRCh. 2 - Prob. 18CRCh. 2 - Prob. 19CRCh. 2 - Prob. 20CRCh. 2 - Prob. 21CRCh. 2 - Prob. 22CRCh. 2 - Prob. 23CRCh. 2 - Prob. 24CRCh. 2 - Prob. 25CRCh. 2 - Prob. 26CRCh. 2 - Prob. 27CRCh. 2 - Prob. 28CRCh. 2 - Prob. 29CRCh. 2 - Prob. 30CRCh. 2 - Prob. 31CRCh. 2 - Prob. 32CRCh. 2 - Prob. 33CRCh. 2 - Prob. 34CRCh. 2 - Prob. 35CRCh. 2 - Prob. 36CRCh. 2 - Prob. 37CRCh. 2 - Prob. 38CRCh. 2 - Prob. 39CRCh. 2 - Prob. 40CRCh. 2 - Prob. 41CRCh. 2 - Prob. 42CRCh. 2 - Prob. 43CRCh. 2 - Prob. 44CRCh. 2 - Prob. 45CRCh. 2 - Prob. 46CRCh. 2 - Prob. 47CRCh. 2 - Prob. 48CRCh. 2 - Prob. 49CRCh. 2 - Prob. 50CRCh. 2 - Prob. 51CRCh. 2 - Prob. 52CRCh. 2 - Prob. 53CRCh. 2 - Prob. 54CRCh. 2 - Prob. 55CRCh. 2 - Prob. 56CRCh. 2 - Prob. 57CRCh. 2 - Prob. 58CRCh. 2 - Prob. 59CRCh. 2 - Prob. 60CRCh. 2 - Prob. 61CRCh. 2 - Prob. 62CRCh. 2 - Prob. 63CRCh. 2 - Prob. 64CRCh. 2 - Prob. 65CRCh. 2 - Prob. 66CRCh. 2 - Prob. 67CRCh. 2 - Prob. 68CRCh. 2 - Prob. 69CRCh. 2 - Prob. 70CRCh. 2 - Prob. 71CRCh. 2 - Prob. 72CRCh. 2 - Prob. 73CRCh. 2 - Prob. 74CRCh. 2 - Prob. 75CRCh. 2 - Prob. 76CRCh. 2 - Prob. 77CRCh. 2 - Prob. 78CRCh. 2 - Prob. 79CRCh. 2 - Prob. 80CRCh. 2 - Prob. 81CRCh. 2 - Prob. 82CRCh. 2 - Prob. 83CRCh. 2 - Prob. 84CRCh. 2 - Prob. 85CRCh. 2 - Prob. 86CRCh. 2 - Prob. 87CRCh. 2 - Prob. 88CRCh. 2 - Prob. 89CRCh. 2 - Prob. 90CRCh. 2 - Prob. 91CRCh. 2 - Prob. 92CRCh. 2 - Prob. 93CRCh. 2 - Prob. 94CRCh. 2 - Prob. 95CRCh. 2 - Prob. 96CRCh. 2 - Prob. 97CRCh. 2 - Prob. 98CRCh. 2 - Prob. 99CRCh. 2 - Prob. 100CRCh. 2 - Prob. 101CRCh. 2 - Prob. 102CRCh. 2 - Prob. 103CRCh. 2 - Prob. 104CRCh. 2 - Prob. 105CRCh. 2 - Prob. 106CRCh. 2 - Prob. 107CRCh. 2 - Prob. 108CRCh. 2 - Prob. 109CRCh. 2 - Prob. 110CRCh. 2 - Prob. 111CRCh. 2 - Prob. 112CRCh. 2 - Prob. 113CRCh. 2 - Prob. 114CRCh. 2 - Prob. 115CRCh. 2 - Prob. 116CRCh. 2 - Prob. 117CRCh. 2 - Prob. 118CRCh. 2 - Prob. 119CRCh. 2 - Prob. 120CRCh. 2 - Prob. 121CRCh. 2 - Prob. 122CRCh. 2 - Prob. 123CRCh. 2 - Prob. 124CRCh. 2 - Prob. 125CRCh. 2 - Prob. 126CRCh. 2 - Prob. 127CRCh. 2 - Prob. 128CRCh. 2 - Prob. 129CRCh. 2 - Prob. 130CRCh. 2 - Prob. 131CRCh. 2 - Prob. 132CRCh. 2 - Prob. 133CRCh. 2 - Prob. 134CRCh. 2 - Prob. 135CRCh. 2 - Prob. 136CRCh. 2 - Prob. 137CRCh. 2 - Prob. 138CRCh. 2 - Prob. 139CRCh. 2 - Prob. 140CRCh. 2 - Prob. 141CRCh. 2 - Prob. 142CRCh. 2 - Prob. 143CRCh. 2 - Prob. 144CRCh. 2 - Prob. 145CRCh. 2 - Prob. 146CRCh. 2 - Prob. 147CRCh. 2 - Prob. 148CRCh. 2 - Prob. 149CRCh. 2 - Prob. 150CRCh. 2 - Prob. 151CRCh. 2 - Prob. 152CRCh. 2 - Prob. 153CRCh. 2 - Prob. 154CRCh. 2 - Prob. 155CRCh. 2 - Prob. 156CRCh. 2 - Prob. 157CRCh. 2 - Prob. 158CRCh. 2 - Prob. 159CRCh. 2 - Prob. 160CRCh. 2 - Prob. 161CRCh. 2 - Prob. 162CRCh. 2 - Prob. 163CRCh. 2 - Prob. 164CRCh. 2 - Prob. 165CRCh. 2 - Prob. 166CRCh. 2 - Prob. 1CTCh. 2 - Prob. 2CTCh. 2 - Prob. 3CTCh. 2 - Prob. 4CTCh. 2 - Prob. 5CTCh. 2 - Prob. 6CTCh. 2 - Prob. 7CTCh. 2 - Prob. 8CTCh. 2 - Prob. 9CTCh. 2 - Prob. 10CTCh. 2 - Prob. 11CTCh. 2 - Prob. 12CTCh. 2 - Prob. 13CTCh. 2 - Prob. 14CTCh. 2 - Prob. 15CTCh. 2 - Prob. 16CTCh. 2 - Prob. 17CTCh. 2 - Prob. 18CTCh. 2 - Prob. 19CTCh. 2 - Prob. 20CTCh. 2 - Prob. 21CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 1. One of the partial fractions for 2 4x²+x-9 x3+2x²-3x 2 x+1 a) x23 b) x 1½ c) x² d) x-1 x isarrow_forward1. One of the partial fractions for 2 2 4x²+x-9 x3+2x²-3x a) x3 b) x11 c) x² d) z x-1 2. Identify the improper integral. 1 x 2 x dx a) 3x dx b) f² 3x dx 0 3-2x 0 3-2x x is c) √2^: 4 √232x dx d) fo² 3x dx 1 1 0 3-2x B. So eax dx converges to if : a) O if a0 c) - 1½ ifa 0arrow_forwardComplete the square and find the indefinite integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) dx x²-12x+27arrow_forward
- Complete the table. Enter DNE if a quantity doesn't exist or NEI if not enough information is given. f(c) limx-->c- f(x) limx-->c+ f(x) limx -->c f(x) continuity at x=c 2 4arrow_forwardFind the indefinite integral. (Use C for the constant of integration.) 9x arcsin(x) dxarrow_forwardFind the indefinite integral using the substitution x = 5 sin(e). (Use C for the constant of integration.) 1 dx (25-x²)3/2arrow_forward
- Find the indefinite integral using the substitution x = 7 sec(0). (Use C for the constant of integration.) √ ׳ √x² - 49 dxarrow_forward2 Graph of h 6. The graph of the function h is given in the xy-plane. Which of the following statements is correct? , the graph of h is increasing at an increasing rate. (A) For (B) For (C) For 苏|4 K|4 π π , the graph of h is increasing at a decreasing rate. 2 0 and b>1 (B) a>0 and 01 (D) a<0 and 0arrow_forward3. Consider the sequences of functions fn: [-T, π] → R, sin(n²x) n(2) n (i) Find a function f : [-T, π] R such that fnf pointwise as n∞. Further, show that f uniformly on [-T,π] as n→ ∞. [20 Marks] (ii) Does the sequence of derivatives f(x) has a pointwise limit on [-7,π]? Justify your answer. [10 Marks]arrow_forwardGood Day, Please assist with the following. Regards,arrow_forwardFor each given function f(x) find f'(x) using the rules learned in section 9.5. 1. f(x)=x32 32x 2. f(x)=7x+13 3. f(x) = x4 4. f(x) = √√x³ 5. f(x) = 3x²+ 3 x2arrow_forwardFind: lim x →-6 f (x) limx-4 f (x) lim x-1 f (x) lim x →4 f (x) (-6,3) • (-1,5) -8 -7 (-6,-2) 4+ (4,5) (4,2) • (-1,1) -6arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Polynomials with Trigonometric Solutions (2 of 3: Substitute & solve); Author: Eddie Woo;https://www.youtube.com/watch?v=EnfhYp4o20w;License: Standard YouTube License, CC-BY
Quick Revision of Polynomials | Tricks to Solve Polynomials in Algebra | Maths Tricks | Letstute; Author: Let'stute;https://www.youtube.com/watch?v=YmDnGcol-gs;License: Standard YouTube License, CC-BY
Introduction to Polynomials; Author: Professor Dave Explains;https://www.youtube.com/watch?v=nPPNgin7W7Y;License: Standard Youtube License