EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR

8th Edition

ISBN: 9780357022078

Author: Larson

Publisher: CENGAGE L

See similar textbooks

Concept explainers

Minimization

In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…

Maxima and Minima

The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.

Derivatives

A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …

Concavity

In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …

Videos

Question

Chapter 2.5, Problem 76E

To determine

To find: The possible translation of equation so that function has four distinct real zeroes.

Expert Solution

Answer to Problem 76E

f(x)=x4−4x2+e such that e∈(0,4)

Explanation of Solution

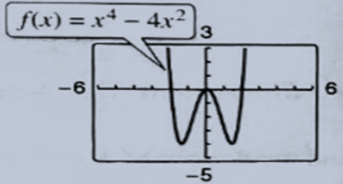
Given information:

The given graph has an equation of f(x)=x4−4x2

Formula used:

f(x)=x4−4x2+a

Given equation is a polynomial equation with degree 4 .

The standard form of a polynomial in 4^t^h degree will be ax4+bx3+cx2+dx+e.

By definition, a 4 th degree polynomial equation always has 4 roots.

As asked in the question, for translating an equation,change is made in the constant that is e.

For four distinct real zeroes the graph should attain value of f(x) as zero four times that is it should touch the x-axis 4 times.

Looking at the graph it can be derived that if the value e has any value between 0 and 4 excluding 0 and 4 it will give 4 zeroes

EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR, Chapter 2.5, Problem 76E , additional homework tip 1

Conclusion:

For having four real distinct zeroes the equation must be translated as f(x)=x4−4x2+e such that e∈(0,4) .

To determine

To find: The possible translation of equation so that function has two real zeroes, each of multiplicity 2 .

Expert Solution

Answer to Problem 76E

f(x)=x4−4x2+4

Explanation of Solution

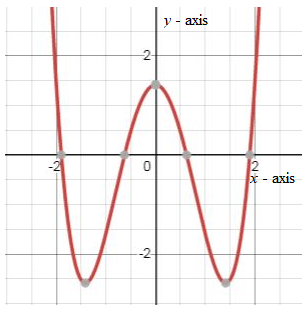
Given information:

The given graph has an equation of f(x)=x4−4x2

Formula used:

f(x)=x4−4x2+a

Given equation is a polynomial equation with degree 4 .

The standard form of a polynomial in 4 th degree will be ax4+bx3+cx2+dx+e.

By definition, a 4 th degree polynomial equation always has 4 roots.

As asked in the question, for translating an equation change is made in the constant that is e.

For having 2 real zeroes and 2 imaginary zeroes each of multiplicity 2 , e can have only one specific value as 4.

The graph will touch at x-axis at only 2 points that is 2 and −2.

The remaining two roots will be imaginary.

EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR, Chapter 2.5, Problem 76E , additional homework tip 2

Conclusion:

To translate the graph in such a way that it has two real zeroes each of multiplicity it should be written/translated as f(x)=x4−4x2+4 .

To determine

To find: The possible translation of equation so that function has two real zeroes and two imaginary zeroes.

Expert Solution

Answer to Problem 76E

f(x)=x4−4x2+e such that e∈(−∞,0)

Explanation of Solution

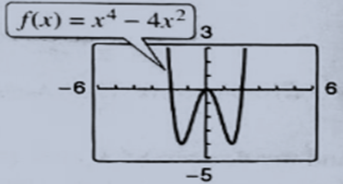
Given information:

The given graph has an equation of f(x)=x4−4x2

Formula used:

f(x)=x4−4x2+a

Given equation is a polynomial equation with degree 4 .

The standard form of a polynomial in 4 th degree will be ax4+bx3+cx2+dx+e.

By definition, a 4 th degree polynomial equation always has 4 roots.

As asked in the question, for translating an equation change is made in the constant that is e.

For having 2 real and 2 imaginary zeroes the graph should touch x-axis only at two points.

For doing so the graph should be moved towards negative y-axis such that e has value between −∞ and 0 excluding the extreme values.

EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR, Chapter 2.5, Problem 76E , additional homework tip 3

Conclusion:

To translate the equation such that it has 2 real and 2 imaginary zeroes, the equation must be written as f(x)=x4−4x2+e such that e∈(−∞,0) .

Here the negative sign indicates that the graph has to be moved towards the negative y-axis.

To determine

To find: The possible translation of equation so that function has four imaginary zeroes.

Expert Solution

Answer to Problem 76E

f(x)=x4−4x2+e such that e∈(4,∞)

Explanation of Solution

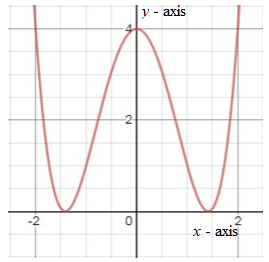
Given information:

The given graph has an equation of f(x)=x4−4x2

Formula used:

f(x)=x4−4x2+a

Given equation is a polynomial equation with degree 4 .

The standard form of a polynomial in 4 th degree will be ax4+bx3+cx2+dx+e.

By definition, a 4 th degree polynomial equation always has 4 roots.

As asked in the question, for translating an equation change is made in the constant that is e.

For having all 4 zeroes as imaginary the graph should not touch the x-axis at any point.

This can be achieved only if the value of e is greater than 4 up to infinity.

EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR, Chapter 2.5, Problem 76E , additional homework tip 4

Conclusion:

The equation must be translated as f(x)=x4−4x2+e such that e∈(4,∞) to obtain 4 imaginary zeroes.

Chapter 2.5, Problem 75E

Chapter 2.5, Problem 77E

Chapter 2 Solutions

EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR

Ch. 2.1 - Prob. 1E Ch. 2.1 - Prob. 2E Ch. 2.1 - Prob. 3E Ch. 2.1 - Prob. 4E Ch. 2.1 - Prob. 5E Ch. 2.1 - Prob. 6E Ch. 2.1 - Prob. 7E Ch. 2.1 - Prob. 8E Ch. 2.1 - Prob. 9E Ch. 2.1 - Prob. 10E

Ch. 2.1 - Prob. 11E Ch. 2.1 - Prob. 12E Ch. 2.1 - Prob. 13E Ch. 2.1 - Prob. 14E Ch. 2.1 - Prob. 15E Ch. 2.1 - Prob. 16E Ch. 2.1 - Prob. 17E Ch. 2.1 - Prob. 18E Ch. 2.1 - Prob. 19E Ch. 2.1 - Prob. 20E Ch. 2.1 - Prob. 21E Ch. 2.1 - Prob. 22E Ch. 2.1 - Prob. 23E Ch. 2.1 - Prob. 24E Ch. 2.1 - Prob. 25E Ch. 2.1 - Prob. 26E Ch. 2.1 - Prob. 27E Ch. 2.1 - Prob. 28E Ch. 2.1 - Prob. 29E Ch. 2.1 - Prob. 30E Ch. 2.1 - Prob. 31E Ch. 2.1 - Prob. 32E Ch. 2.1 - Prob. 33E Ch. 2.1 - Prob. 34E Ch. 2.1 - Prob. 35E Ch. 2.1 - Prob. 36E Ch. 2.1 - Prob. 37E Ch. 2.1 - Prob. 38E Ch. 2.1 - Prob. 39E Ch. 2.1 - Prob. 40E Ch. 2.1 - Prob. 41E Ch. 2.1 - Prob. 42E Ch. 2.1 - Prob. 43E Ch. 2.1 - Prob. 44E Ch. 2.1 - Prob. 45E Ch. 2.1 - Prob. 46E Ch. 2.1 - Prob. 47E Ch. 2.1 - Prob. 48E Ch. 2.1 - Prob. 49E Ch. 2.1 - Prob. 50E Ch. 2.1 - Prob. 51E Ch. 2.1 - Prob. 52E Ch. 2.1 - Prob. 53E Ch. 2.1 - Prob. 54E Ch. 2.1 - Prob. 55E Ch. 2.1 - Prob. 56E Ch. 2.1 - Prob. 57E Ch. 2.1 - Prob. 58E Ch. 2.1 - Prob. 59E Ch. 2.1 - Prob. 60E Ch. 2.1 - Prob. 61E Ch. 2.1 - Prob. 62E Ch. 2.1 - Prob. 63E Ch. 2.1 - Prob. 64E Ch. 2.1 - Prob. 65E Ch. 2.1 - Prob. 66E Ch. 2.1 - Prob. 67E Ch. 2.1 - Prob. 68E Ch. 2.1 - Prob. 69E Ch. 2.1 - Prob. 70E Ch. 2.1 - Prob. 71E Ch. 2.1 - Prob. 72E Ch. 2.1 - Prob. 73E Ch. 2.1 - Prob. 74E Ch. 2.1 - Prob. 75E Ch. 2.1 - Prob. 76E Ch. 2.1 - Prob. 77E Ch. 2.1 - Prob. 78E Ch. 2.1 - Prob. 79E Ch. 2.1 - Prob. 80E Ch. 2.1 - Prob. 81E Ch. 2.1 - Prob. 82E Ch. 2.1 - Prob. 83E Ch. 2.1 - Prob. 84E Ch. 2.1 - Prob. 85E Ch. 2.1 - Prob. 86E Ch. 2.1 - Prob. 87E Ch. 2.1 - Prob. 88E Ch. 2.1 - Prob. 89E Ch. 2.2 - Prob. 1E Ch. 2.2 - Prob. 2E Ch. 2.2 - Prob. 3E Ch. 2.2 - Prob. 4E Ch. 2.2 - Prob. 5E Ch. 2.2 - Prob. 6E Ch. 2.2 - Prob. 7E Ch. 2.2 - Prob. 8E Ch. 2.2 - Prob. 9E Ch. 2.2 - Prob. 10E Ch. 2.2 - Prob. 11E Ch. 2.2 - Prob. 12E Ch. 2.2 - Prob. 13E Ch. 2.2 - Prob. 14E Ch. 2.2 - Prob. 15E Ch. 2.2 - Prob. 16E Ch. 2.2 - Prob. 17E Ch. 2.2 - Prob. 18E Ch. 2.2 - Prob. 19E Ch. 2.2 - Prob. 20E Ch. 2.2 - Prob. 21E Ch. 2.2 - Prob. 22E Ch. 2.2 - Prob. 23E Ch. 2.2 - Prob. 24E Ch. 2.2 - Prob. 25E Ch. 2.2 - Prob. 26E Ch. 2.2 - Prob. 27E Ch. 2.2 - Prob. 28E Ch. 2.2 - Prob. 29E Ch. 2.2 - Prob. 30E Ch. 2.2 - Prob. 31E Ch. 2.2 - Prob. 32E Ch. 2.2 - Prob. 33E Ch. 2.2 - Prob. 34E Ch. 2.2 - Prob. 35E Ch. 2.2 - Prob. 36E Ch. 2.2 - Prob. 37E Ch. 2.2 - Prob. 38E Ch. 2.2 - Prob. 39E Ch. 2.2 - Prob. 40E Ch. 2.2 - Prob. 41E Ch. 2.2 - Prob. 42E Ch. 2.2 - Prob. 43E Ch. 2.2 - Prob. 44E Ch. 2.2 - Prob. 45E Ch. 2.2 - Prob. 46E Ch. 2.2 - Prob. 47E Ch. 2.2 - Prob. 48E Ch. 2.2 - Prob. 49E Ch. 2.2 - Prob. 50E Ch. 2.2 - Prob. 51E Ch. 2.2 - Prob. 52E Ch. 2.2 - Prob. 53E Ch. 2.2 - Prob. 54E Ch. 2.2 - Prob. 55E Ch. 2.2 - Prob. 56E Ch. 2.2 - Prob. 57E Ch. 2.2 - Prob. 58E Ch. 2.2 - Prob. 59E Ch. 2.2 - Prob. 60E Ch. 2.2 - Prob. 61E Ch. 2.2 - Prob. 62E Ch. 2.2 - Prob. 63E Ch. 2.2 - Prob. 64E Ch. 2.2 - Prob. 65E Ch. 2.2 - Prob. 66E Ch. 2.2 - Prob. 67E Ch. 2.2 - Prob. 68E Ch. 2.2 - Prob. 69E Ch. 2.2 - Prob. 70E Ch. 2.2 - Prob. 71E Ch. 2.2 - Prob. 72E Ch. 2.2 - Prob. 73E Ch. 2.2 - Prob. 74E Ch. 2.2 - Prob. 75E Ch. 2.2 - Prob. 76E Ch. 2.2 - Prob. 77E Ch. 2.2 - Prob. 78E Ch. 2.2 - Prob. 79E Ch. 2.2 - Prob. 80E Ch. 2.2 - Prob. 81E Ch. 2.2 - Prob. 82E Ch. 2.2 - Prob. 83E Ch. 2.2 - Prob. 84E Ch. 2.2 - Prob. 85E Ch. 2.2 - Prob. 86E Ch. 2.2 - Prob. 87E Ch. 2.2 - Prob. 88E Ch. 2.2 - Prob. 89E Ch. 2.2 - Prob. 90E Ch. 2.2 - Prob. 91E Ch. 2.2 - Prob. 92E Ch. 2.2 - Prob. 93E Ch. 2.2 - Prob. 94E Ch. 2.2 - Prob. 95E Ch. 2.2 - Prob. 96E Ch. 2.2 - Prob. 97E Ch. 2.2 - Prob. 98E Ch. 2.2 - Prob. 99E Ch. 2.2 - Prob. 100E Ch. 2.2 - Prob. 101E Ch. 2.2 - Prob. 102E Ch. 2.2 - Prob. 103E Ch. 2.2 - Prob. 104E Ch. 2.2 - Prob. 105E Ch. 2.2 - Prob. 106E Ch. 2.2 - Prob. 107E Ch. 2.2 - Prob. 108E Ch. 2.2 - Prob. 109E Ch. 2.2 - Prob. 110E Ch. 2.2 - Prob. 111E Ch. 2.2 - Prob. 112E Ch. 2.2 - Prob. 113E Ch. 2.2 - Prob. 114E Ch. 2.2 - Prob. 115E Ch. 2.2 - Prob. 116E Ch. 2.2 - Prob. 117E Ch. 2.2 - Prob. 118E Ch. 2.2 - Prob. 119E Ch. 2.2 - Prob. 120E Ch. 2.2 - Prob. 121E Ch. 2.2 - Prob. 122E Ch. 2.2 - Prob. 123E Ch. 2.2 - Prob. 124E Ch. 2.2 - Prob. 125E Ch. 2.2 - Prob. 126E Ch. 2.2 - Prob. 127E Ch. 2.2 - Prob. 128E Ch. 2.3 - Prob. 1E Ch. 2.3 - Prob. 2E Ch. 2.3 - Prob. 3E Ch. 2.3 - Prob. 4E Ch. 2.3 - Prob. 5E Ch. 2.3 - Prob. 6E Ch. 2.3 - Prob. 7E Ch. 2.3 - Prob. 8E Ch. 2.3 - Prob. 9E Ch. 2.3 - Prob. 10E Ch. 2.3 - Prob. 11E Ch. 2.3 - Prob. 12E Ch. 2.3 - Prob. 13E Ch. 2.3 - Prob. 14E Ch. 2.3 - Prob. 15E Ch. 2.3 - Prob. 16E Ch. 2.3 - Prob. 17E Ch. 2.3 - Prob. 18E Ch. 2.3 - Prob. 19E Ch. 2.3 - Prob. 20E Ch. 2.3 - Prob. 21E Ch. 2.3 - Prob. 22E Ch. 2.3 - Prob. 23E Ch. 2.3 - Prob. 24E Ch. 2.3 - Prob. 25E Ch. 2.3 - Prob. 26E Ch. 2.3 - Prob. 27E Ch. 2.3 - Prob. 28E Ch. 2.3 - Prob. 29E Ch. 2.3 - Prob. 30E Ch. 2.3 - Prob. 31E Ch. 2.3 - Prob. 32E Ch. 2.3 - Prob. 33E Ch. 2.3 - Prob. 34E Ch. 2.3 - Prob. 35E Ch. 2.3 - Prob. 36E Ch. 2.3 - Prob. 37E Ch. 2.3 - Prob. 38E Ch. 2.3 - Prob. 39E Ch. 2.3 - Prob. 40E Ch. 2.3 - Prob. 41E Ch. 2.3 - Prob. 42E Ch. 2.3 - Prob. 43E Ch. 2.3 - Prob. 44E Ch. 2.3 - Prob. 45E Ch. 2.3 - Prob. 46E Ch. 2.3 - Prob. 47E Ch. 2.3 - Prob. 48E Ch. 2.3 - Prob. 49E Ch. 2.3 - Prob. 50E Ch. 2.3 - Prob. 51E Ch. 2.3 - Prob. 52E Ch. 2.3 - Prob. 53E Ch. 2.3 - Prob. 54E Ch. 2.3 - Prob. 55E Ch. 2.3 - Prob. 56E Ch. 2.3 - Prob. 57E Ch. 2.3 - Prob. 58E Ch. 2.3 - Prob. 59E Ch. 2.3 - Prob. 60E Ch. 2.3 - Prob. 61E Ch. 2.3 - Prob. 62E Ch. 2.3 - Prob. 63E Ch. 2.3 - Prob. 64E Ch. 2.3 - Prob. 65E Ch. 2.3 - Prob. 66E Ch. 2.3 - Prob. 67E Ch. 2.3 - Prob. 68E Ch. 2.3 - Prob. 69E Ch. 2.3 - Prob. 70E Ch. 2.3 - Prob. 71E Ch. 2.3 - Prob. 72E Ch. 2.3 - Prob. 73E Ch. 2.3 - Prob. 74E Ch. 2.3 - Prob. 75E Ch. 2.3 - Prob. 76E Ch. 2.3 - Prob. 77E Ch. 2.3 - Prob. 78E Ch. 2.3 - Prob. 79E Ch. 2.3 - Prob. 80E Ch. 2.3 - Prob. 81E Ch. 2.3 - Prob. 82E Ch. 2.3 - Prob. 83E Ch. 2.3 - Prob. 84E Ch. 2.3 - Prob. 85E Ch. 2.3 - Prob. 86E Ch. 2.3 - Prob. 87E Ch. 2.3 - Prob. 88E Ch. 2.3 - Prob. 89E Ch. 2.3 - Prob. 90E Ch. 2.3 - Prob. 91E Ch. 2.3 - Prob. 92E Ch. 2.3 - Prob. 93E Ch. 2.3 - Prob. 94E Ch. 2.3 - Prob. 95E Ch. 2.3 - Prob. 96E Ch. 2.3 - Prob. 97E Ch. 2.3 - Prob. 98E Ch. 2.3 - Prob. 99E Ch. 2.3 - Prob. 100E Ch. 2.3 - Prob. 101E Ch. 2.3 - Prob. 102E Ch. 2.3 - Prob. 103E Ch. 2.3 - Prob. 104E Ch. 2.3 - Prob. 105E Ch. 2.3 - Prob. 106E Ch. 2.3 - Prob. 107E Ch. 2.3 - Prob. 108E Ch. 2.3 - Prob. 109E Ch. 2.3 - Prob. 110E Ch. 2.3 - Prob. 111E Ch. 2.3 - Prob. 112E Ch. 2.3 - Prob. 113E Ch. 2.3 - Prob. 114E Ch. 2.3 - Prob. 115E Ch. 2.3 - Prob. 116E Ch. 2.3 - Prob. 117E Ch. 2.3 - Prob. 118E Ch. 2.3 - Prob. 119E Ch. 2.3 - Prob. 120E Ch. 2.4 - Prob. 1E Ch. 2.4 - Prob. 2E Ch. 2.4 - Prob. 3E Ch. 2.4 - Prob. 4E Ch. 2.4 - Prob. 5E Ch. 2.4 - Prob. 6E Ch. 2.4 - Prob. 7E Ch. 2.4 - Prob. 8E Ch. 2.4 - Prob. 9E Ch. 2.4 - Prob. 10E Ch. 2.4 - Prob. 11E Ch. 2.4 - Prob. 12E Ch. 2.4 - Prob. 13E Ch. 2.4 - Prob. 14E Ch. 2.4 - Prob. 15E Ch. 2.4 - Prob. 16E Ch. 2.4 - Prob. 17E Ch. 2.4 - Prob. 18E Ch. 2.4 - Prob. 19E Ch. 2.4 - Prob. 20E Ch. 2.4 - Prob. 21E Ch. 2.4 - Prob. 22E Ch. 2.4 - Prob. 23E Ch. 2.4 - Prob. 24E Ch. 2.4 - Prob. 25E Ch. 2.4 - Prob. 26E Ch. 2.4 - Prob. 27E Ch. 2.4 - Prob. 28E Ch. 2.4 - Prob. 29E Ch. 2.4 - Prob. 30E Ch. 2.4 - Prob. 31E Ch. 2.4 - Prob. 32E Ch. 2.4 - Prob. 33E Ch. 2.4 - Prob. 34E Ch. 2.4 - Prob. 35E Ch. 2.4 - Prob. 36E Ch. 2.4 - Prob. 37E Ch. 2.4 - Prob. 38E Ch. 2.4 - Prob. 39E Ch. 2.4 - Prob. 40E Ch. 2.4 - Prob. 41E Ch. 2.4 - Prob. 42E Ch. 2.4 - Prob. 43E Ch. 2.4 - Prob. 44E Ch. 2.4 - Prob. 45E Ch. 2.4 - Prob. 46E Ch. 2.4 - Prob. 47E Ch. 2.4 - Prob. 48E Ch. 2.4 - Prob. 49E Ch. 2.4 - Prob. 50E Ch. 2.4 - Prob. 51E Ch. 2.4 - Prob. 52E Ch. 2.4 - Prob. 53E Ch. 2.4 - Prob. 54E Ch. 2.4 - Prob. 55E Ch. 2.4 - Prob. 56E Ch. 2.4 - Prob. 57E Ch. 2.4 - Prob. 58E Ch. 2.4 - Prob. 59E Ch. 2.4 - Prob. 60E Ch. 2.4 - Prob. 61E Ch. 2.4 - Prob. 62E Ch. 2.4 - Prob. 63E Ch. 2.4 - Prob. 64E Ch. 2.4 - Prob. 65E Ch. 2.4 - Prob. 66E Ch. 2.4 - Prob. 67E Ch. 2.4 - Prob. 68E Ch. 2.4 - Prob. 69E Ch. 2.4 - Prob. 70E Ch. 2.4 - Prob. 71E Ch. 2.4 - Prob. 72E Ch. 2.4 - Prob. 73E Ch. 2.4 - Prob. 74E Ch. 2.4 - Prob. 75E Ch. 2.4 - Prob. 76E Ch. 2.4 - Prob. 77E Ch. 2.4 - Prob. 78E Ch. 2.4 - Prob. 79E Ch. 2.4 - Prob. 80E Ch. 2.4 - Prob. 81E Ch. 2.4 - Prob. 82E Ch. 2.4 - Prob. 83E Ch. 2.4 - Prob. 84E Ch. 2.4 - Prob. 85E Ch. 2.4 - Prob. 86E Ch. 2.4 - Prob. 87E Ch. 2.4 - Prob. 88E Ch. 2.4 - Prob. 89E Ch. 2.4 - Prob. 90E Ch. 2.4 - Prob. 91E Ch. 2.4 - Prob. 92E Ch. 2.4 - Prob. 93E Ch. 2.4 - Prob. 94E Ch. 2.4 - Prob. 95E Ch. 2.4 - Prob. 96E Ch. 2.4 - Prob. 97E Ch. 2.4 - Prob. 98E Ch. 2.5 - Prob. 1E Ch. 2.5 - Prob. 2E Ch. 2.5 - Prob. 3E Ch. 2.5 - Prob. 4E Ch. 2.5 - Prob. 5E Ch. 2.5 - Prob. 6E Ch. 2.5 - Prob. 7E Ch. 2.5 - Prob. 8E Ch. 2.5 - Prob. 9E Ch. 2.5 - Prob. 10E Ch. 2.5 - Prob. 11E Ch. 2.5 - Prob. 12E Ch. 2.5 - Prob. 13E Ch. 2.5 - Prob. 14E Ch. 2.5 - Prob. 15E Ch. 2.5 - Prob. 16E Ch. 2.5 - Prob. 17E Ch. 2.5 - Prob. 18E Ch. 2.5 - Prob. 19E Ch. 2.5 - Prob. 20E Ch. 2.5 - Prob. 21E Ch. 2.5 - Prob. 22E Ch. 2.5 - Prob. 23E Ch. 2.5 - Prob. 24E Ch. 2.5 - Prob. 25E Ch. 2.5 - Prob. 26E Ch. 2.5 - Prob. 27E Ch. 2.5 - Prob. 28E Ch. 2.5 - Prob. 29E Ch. 2.5 - Prob. 30E Ch. 2.5 - Prob. 31E Ch. 2.5 - Prob. 32E Ch. 2.5 - Prob. 33E Ch. 2.5 - Prob. 34E Ch. 2.5 - Prob. 35E Ch. 2.5 - Prob. 36E Ch. 2.5 - Prob. 37E Ch. 2.5 - Prob. 38E Ch. 2.5 - Prob. 39E Ch. 2.5 - Prob. 40E Ch. 2.5 - Prob. 41E Ch. 2.5 - Prob. 42E Ch. 2.5 - Prob. 43E Ch. 2.5 - Prob. 44E Ch. 2.5 - Prob. 45E Ch. 2.5 - Prob. 46E Ch. 2.5 - Prob. 47E Ch. 2.5 - Prob. 48E Ch. 2.5 - Prob. 49E Ch. 2.5 - Prob. 50E Ch. 2.5 - Prob. 51E Ch. 2.5 - Prob. 52E Ch. 2.5 - Prob. 53E Ch. 2.5 - Prob. 54E Ch. 2.5 - Prob. 55E Ch. 2.5 - Prob. 56E Ch. 2.5 - Prob. 57E Ch. 2.5 - Prob. 58E Ch. 2.5 - Prob. 59E Ch. 2.5 - Prob. 60E Ch. 2.5 - Prob. 61E Ch. 2.5 - Prob. 62E Ch. 2.5 - Prob. 63E Ch. 2.5 - Prob. 64E Ch. 2.5 - Prob. 65E Ch. 2.5 - Prob. 66E Ch. 2.5 - Prob. 67E Ch. 2.5 - Prob. 68E Ch. 2.5 - Prob. 69E Ch. 2.5 - Prob. 70E Ch. 2.5 - Prob. 71E Ch. 2.5 - Prob. 72E Ch. 2.5 - Prob. 73E Ch. 2.5 - Prob. 74E Ch. 2.5 - Prob. 75E Ch. 2.5 - Prob. 76E Ch. 2.5 - Prob. 77E Ch. 2.5 - Prob. 78E Ch. 2.6 - Prob. 1E Ch. 2.6 - Prob. 2E Ch. 2.6 - Prob. 3E Ch. 2.6 - Prob. 4E Ch. 2.6 - Prob. 5E Ch. 2.6 - Prob. 6E Ch. 2.6 - Prob. 7E Ch. 2.6 - Prob. 8E Ch. 2.6 - Prob. 9E Ch. 2.6 - Prob. 10E Ch. 2.6 - Prob. 11E Ch. 2.6 - Prob. 12E Ch. 2.6 - Prob. 13E Ch. 2.6 - Prob. 14E Ch. 2.6 - Prob. 15E Ch. 2.6 - Prob. 16E Ch. 2.6 - Prob. 17E Ch. 2.6 - Prob. 18E Ch. 2.6 - Prob. 19E Ch. 2.6 - Prob. 20E Ch. 2.6 - Prob. 21E Ch. 2.6 - Prob. 22E Ch. 2.6 - Prob. 23E Ch. 2.6 - Prob. 24E Ch. 2.6 - Prob. 25E Ch. 2.6 - Prob. 26E Ch. 2.6 - Prob. 27E Ch. 2.6 - Prob. 28E Ch. 2.6 - Prob. 29E Ch. 2.6 - Prob. 30E Ch. 2.6 - Prob. 31E Ch. 2.6 - Prob. 32E Ch. 2.6 - Prob. 33E Ch. 2.6 - Prob. 34E Ch. 2.6 - Prob. 35E Ch. 2.6 - Prob. 36E Ch. 2.6 - Prob. 37E Ch. 2.6 - Prob. 38E Ch. 2.6 - Prob. 39E Ch. 2.6 - Prob. 40E Ch. 2.6 - Prob. 41E Ch. 2.6 - Prob. 42E Ch. 2.6 - Prob. 43E Ch. 2.6 - Prob. 44E Ch. 2.6 - Prob. 45E Ch. 2.6 - Prob. 46E Ch. 2.6 - Prob. 47E Ch. 2.6 - Prob. 48E Ch. 2.6 - Prob. 49E Ch. 2.6 - Prob. 50E Ch. 2.6 - Prob. 51E Ch. 2.6 - Prob. 52E Ch. 2.6 - Prob. 53E Ch. 2.6 - Prob. 54E Ch. 2.6 - Prob. 55E Ch. 2.6 - Prob. 56E Ch. 2.6 - Prob. 57E Ch. 2.6 - Prob. 58E Ch. 2.6 - Prob. 59E Ch. 2.6 - Prob. 60E Ch. 2.6 - Prob. 61E Ch. 2.6 - Prob. 62E Ch. 2.6 - Prob. 63E Ch. 2.6 - Prob. 64E Ch. 2.6 - Prob. 65E Ch. 2.6 - Prob. 66E Ch. 2.7 - Prob. 1E Ch. 2.7 - Prob. 2E Ch. 2.7 - Prob. 3E Ch. 2.7 - Prob. 4E Ch. 2.7 - Prob. 5E Ch. 2.7 - Prob. 6E Ch. 2.7 - Prob. 7E Ch. 2.7 - Prob. 8E Ch. 2.7 - Prob. 9E Ch. 2.7 - Prob. 10E Ch. 2.7 - Prob. 11E Ch. 2.7 - Prob. 12E Ch. 2.7 - Prob. 13E Ch. 2.7 - Prob. 14E Ch. 2.7 - Prob. 15E Ch. 2.7 - Prob. 16E Ch. 2.7 - Prob. 17E Ch. 2.7 - Prob. 18E Ch. 2.7 - Prob. 19E Ch. 2.7 - Prob. 20E Ch. 2.7 - Prob. 21E Ch. 2.7 - Prob. 22E Ch. 2.7 - Prob. 23E Ch. 2.7 - Prob. 24E Ch. 2.7 - Prob. 25E Ch. 2.7 - Prob. 26E Ch. 2.7 - Prob. 27E Ch. 2.7 - Prob. 28E Ch. 2.7 - Prob. 29E Ch. 2.7 - Prob. 30E Ch. 2.7 - Prob. 31E Ch. 2.7 - Prob. 32E Ch. 2.7 - Prob. 33E Ch. 2.7 - Prob. 34E Ch. 2.7 - Prob. 35E Ch. 2.7 - Prob. 36E Ch. 2.7 - Prob. 37E Ch. 2.7 - Prob. 38E Ch. 2.7 - Prob. 39E Ch. 2.7 - Prob. 40E Ch. 2.7 - Prob. 41E Ch. 2.7 - Prob. 42E Ch. 2.7 - Prob. 43E Ch. 2.7 - Prob. 44E Ch. 2.7 - Prob. 45E Ch. 2.7 - Prob. 46E Ch. 2.7 - Prob. 47E Ch. 2.7 - Prob. 48E Ch. 2.7 - Prob. 49E Ch. 2.7 - Prob. 50E Ch. 2.7 - Prob. 51E Ch. 2.7 - Prob. 52E Ch. 2.7 - Prob. 53E Ch. 2.7 - Prob. 54E Ch. 2.7 - Prob. 55E Ch. 2.7 - Prob. 56E Ch. 2.7 - Prob. 57E Ch. 2.7 - Prob. 58E Ch. 2.7 - Prob. 59E Ch. 2.7 - Prob. 60E Ch. 2.7 - Prob. 61E Ch. 2.7 - Prob. 62E Ch. 2.7 - Prob. 63E Ch. 2.7 - Prob. 64E Ch. 2.7 - Prob. 65E Ch. 2.7 - Prob. 66E Ch. 2.7 - Prob. 67E Ch. 2.7 - Prob. 68E Ch. 2.7 - Prob. 69E Ch. 2.7 - Prob. 70E Ch. 2.7 - Prob. 71E Ch. 2.7 - Prob. 72E Ch. 2.7 - Prob. 73E Ch. 2.7 - Prob. 74E Ch. 2.7 - Prob. 75E Ch. 2.7 - Prob. 76E Ch. 2.7 - Prob. 77E Ch. 2.7 - Prob. 78E Ch. 2.7 - Prob. 79E Ch. 2.7 - Prob. 80E Ch. 2.7 - Prob. 81E Ch. 2.7 - Prob. 82E Ch. 2.7 - Prob. 83E Ch. 2.7 - Prob. 84E Ch. 2.7 - Prob. 85E Ch. 2.7 - Prob. 86E Ch. 2.7 - Prob. 87E Ch. 2.7 - Prob. 88E Ch. 2.7 - Prob. 89E Ch. 2.7 - Prob. 90E Ch. 2.7 - Prob. 91E Ch. 2.7 - Prob. 92E Ch. 2.7 - Prob. 93E Ch. 2.7 - Prob. 94E Ch. 2.7 - Prob. 95E Ch. 2.7 - Prob. 96E Ch. 2.7 - Prob. 97E Ch. 2.7 - Prob. 98E Ch. 2.7 - Prob. 99E Ch. 2.7 - Prob. 100E Ch. 2.7 - Prob. 101E Ch. 2.8 - Prob. 1E Ch. 2.8 - Prob. 2E Ch. 2.8 - Prob. 3E Ch. 2.8 - Prob. 4E Ch. 2.8 - Prob. 5E Ch. 2.8 - Prob. 6E Ch. 2.8 - Prob. 7E Ch. 2.8 - Prob. 8E Ch. 2.8 - Prob. 9E Ch. 2.8 - Prob. 10E Ch. 2.8 - Prob. 11E Ch. 2.8 - Prob. 12E Ch. 2.8 - Prob. 13E Ch. 2.8 - Prob. 14E Ch. 2.8 - Prob. 15E Ch. 2.8 - Prob. 16E Ch. 2.8 - Prob. 17E Ch. 2.8 - Prob. 18E Ch. 2.8 - Prob. 19E Ch. 2.8 - Prob. 20E Ch. 2.8 - Prob. 21E Ch. 2.8 - Prob. 22E Ch. 2.8 - Prob. 23E Ch. 2.8 - Prob. 24E Ch. 2.8 - Prob. 25E Ch. 2.8 - Prob. 26E Ch. 2.8 - Prob. 27E Ch. 2.8 - Prob. 28E Ch. 2.8 - Prob. 29E Ch. 2.8 - Prob. 30E Ch. 2.8 - Prob. 31E Ch. 2.8 - Prob. 32E Ch. 2.8 - Prob. 33E Ch. 2.8 - Prob. 34E Ch. 2.8 - Prob. 35E Ch. 2.8 - Prob. 36E Ch. 2.8 - Prob. 37E Ch. 2.8 - Prob. 38E Ch. 2.8 - Prob. 39E Ch. 2.8 - Prob. 40E Ch. 2 - Prob. 1CR Ch. 2 - Prob. 2CR Ch. 2 - Prob. 3CR Ch. 2 - Prob. 4CR Ch. 2 - Prob. 5CR Ch. 2 - Prob. 6CR Ch. 2 - Prob. 7CR Ch. 2 - Prob. 8CR Ch. 2 - Prob. 9CR Ch. 2 - Prob. 10CR Ch. 2 - Prob. 11CR Ch. 2 - Prob. 12CR Ch. 2 - Prob. 13CR Ch. 2 - Prob. 14CR Ch. 2 - Prob. 15CR Ch. 2 - Prob. 16CR Ch. 2 - Prob. 17CR Ch. 2 - Prob. 18CR Ch. 2 - Prob. 19CR Ch. 2 - Prob. 20CR Ch. 2 - Prob. 21CR Ch. 2 - Prob. 22CR Ch. 2 - Prob. 23CR Ch. 2 - Prob. 24CR Ch. 2 - Prob. 25CR Ch. 2 - Prob. 26CR Ch. 2 - Prob. 27CR Ch. 2 - Prob. 28CR Ch. 2 - Prob. 29CR Ch. 2 - Prob. 30CR Ch. 2 - Prob. 31CR Ch. 2 - Prob. 32CR Ch. 2 - Prob. 33CR Ch. 2 - Prob. 34CR Ch. 2 - Prob. 35CR Ch. 2 - Prob. 36CR Ch. 2 - Prob. 37CR Ch. 2 - Prob. 38CR Ch. 2 - Prob. 39CR Ch. 2 - Prob. 40CR Ch. 2 - Prob. 41CR Ch. 2 - Prob. 42CR Ch. 2 - Prob. 43CR Ch. 2 - Prob. 44CR Ch. 2 - Prob. 45CR Ch. 2 - Prob. 46CR Ch. 2 - Prob. 47CR Ch. 2 - Prob. 48CR Ch. 2 - Prob. 49CR Ch. 2 - Prob. 50CR Ch. 2 - Prob. 51CR Ch. 2 - Prob. 52CR Ch. 2 - Prob. 53CR Ch. 2 - Prob. 54CR Ch. 2 - Prob. 55CR Ch. 2 - Prob. 56CR Ch. 2 - Prob. 57CR Ch. 2 - Prob. 58CR Ch. 2 - Prob. 59CR Ch. 2 - Prob. 60CR Ch. 2 - Prob. 61CR Ch. 2 - Prob. 62CR Ch. 2 - Prob. 63CR Ch. 2 - Prob. 64CR Ch. 2 - Prob. 65CR Ch. 2 - Prob. 66CR Ch. 2 - Prob. 67CR Ch. 2 - Prob. 68CR Ch. 2 - Prob. 69CR Ch. 2 - Prob. 70CR Ch. 2 - Prob. 71CR Ch. 2 - Prob. 72CR Ch. 2 - Prob. 73CR Ch. 2 - Prob. 74CR Ch. 2 - Prob. 75CR Ch. 2 - Prob. 76CR Ch. 2 - Prob. 77CR Ch. 2 - Prob. 78CR Ch. 2 - Prob. 79CR Ch. 2 - Prob. 80CR Ch. 2 - Prob. 81CR Ch. 2 - Prob. 82CR Ch. 2 - Prob. 83CR Ch. 2 - Prob. 84CR Ch. 2 - Prob. 85CR Ch. 2 - Prob. 86CR Ch. 2 - Prob. 87CR Ch. 2 - Prob. 88CR Ch. 2 - Prob. 89CR Ch. 2 - Prob. 90CR Ch. 2 - Prob. 91CR Ch. 2 - Prob. 92CR Ch. 2 - Prob. 93CR Ch. 2 - Prob. 94CR Ch. 2 - Prob. 95CR Ch. 2 - Prob. 96CR Ch. 2 - Prob. 97CR Ch. 2 - Prob. 98CR Ch. 2 - Prob. 99CR Ch. 2 - Prob. 100CR Ch. 2 - Prob. 101CR Ch. 2 - Prob. 102CR Ch. 2 - Prob. 103CR Ch. 2 - Prob. 104CR Ch. 2 - Prob. 105CR Ch. 2 - Prob. 106CR Ch. 2 - Prob. 107CR Ch. 2 - Prob. 108CR Ch. 2 - Prob. 109CR Ch. 2 - Prob. 110CR Ch. 2 - Prob. 111CR Ch. 2 - Prob. 112CR Ch. 2 - Prob. 113CR Ch. 2 - Prob. 114CR Ch. 2 - Prob. 115CR Ch. 2 - Prob. 116CR Ch. 2 - Prob. 117CR Ch. 2 - Prob. 118CR Ch. 2 - Prob. 119CR Ch. 2 - Prob. 120CR Ch. 2 - Prob. 121CR Ch. 2 - Prob. 122CR Ch. 2 - Prob. 123CR Ch. 2 - Prob. 124CR Ch. 2 - Prob. 125CR Ch. 2 - Prob. 126CR Ch. 2 - Prob. 127CR Ch. 2 - Prob. 128CR Ch. 2 - Prob. 129CR Ch. 2 - Prob. 130CR Ch. 2 - Prob. 131CR Ch. 2 - Prob. 132CR Ch. 2 - Prob. 133CR Ch. 2 - Prob. 134CR Ch. 2 - Prob. 135CR Ch. 2 - Prob. 136CR Ch. 2 - Prob. 137CR Ch. 2 - Prob. 138CR Ch. 2 - Prob. 139CR Ch. 2 - Prob. 140CR Ch. 2 - Prob. 141CR Ch. 2 - Prob. 142CR Ch. 2 - Prob. 143CR Ch. 2 - Prob. 144CR Ch. 2 - Prob. 145CR Ch. 2 - Prob. 146CR Ch. 2 - Prob. 147CR Ch. 2 - Prob. 148CR Ch. 2 - Prob. 149CR Ch. 2 - Prob. 150CR Ch. 2 - Prob. 151CR Ch. 2 - Prob. 152CR Ch. 2 - Prob. 153CR Ch. 2 - Prob. 154CR Ch. 2 - Prob. 155CR Ch. 2 - Prob. 156CR Ch. 2 - Prob. 157CR Ch. 2 - Prob. 158CR Ch. 2 - Prob. 159CR Ch. 2 - Prob. 160CR Ch. 2 - Prob. 161CR Ch. 2 - Prob. 162CR Ch. 2 - Prob. 163CR Ch. 2 - Prob. 164CR Ch. 2 - Prob. 165CR Ch. 2 - Prob. 166CR Ch. 2 - Prob. 1CT Ch. 2 - Prob. 2CT Ch. 2 - Prob. 3CT Ch. 2 - Prob. 4CT Ch. 2 - Prob. 5CT Ch. 2 - Prob. 6CT Ch. 2 - Prob. 7CT Ch. 2 - Prob. 8CT Ch. 2 - Prob. 9CT Ch. 2 - Prob. 10CT Ch. 2 - Prob. 11CT Ch. 2 - Prob. 12CT Ch. 2 - Prob. 13CT Ch. 2 - Prob. 14CT Ch. 2 - Prob. 15CT Ch. 2 - Prob. 16CT Ch. 2 - Prob. 17CT Ch. 2 - Prob. 18CT Ch. 2 - Prob. 19CT Ch. 2 - Prob. 20CT Ch. 2 - Prob. 21CT

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.