Chapter 2.5, Problem 44E

a.

To determine

Find the zeros of the polynomial function $f(x)=x^3+10x^2+33x+34$ .

Answer to Problem 44E

  $-2,-4+i,-4-i$

Explanation of Solution

Given:

Function: $f(x)=x^3+10x^2+33x+34$

Calculation:

The leading coefficient of given polynomial is 1 and the constant term is 34.

So, possible rational zeros are: $\frac{\text{Factors of}34}{\text{Factors of 1}}=\frac{\pm 1,\pm 2,\pm 17,\pm 34}{\pm 1}=\pm 1,\pm 2,\pm 17,\pm 34$

Using synthetic division to check whether $x=-2$ , is a zero or not.

  $\begin{array}{ccccc}-2& 1& 10& 33& 34\\ & & -2& -16& -34\\ & 1& 8& 17& \boxed{0}\end{array}\begin{array}{c}\\ \\ \hspace{1em}\leftarrow \text{Remainder}\end{array}$

Here, remainder is 0. So, $x=-2$ is a zero of the given polynomial.

So, $f(x)$ factors as

  $f(x)=\left(x+2\right)(x^2+8x+17)$

Now, consider $x^2+8x+17.$

The above polynomial function is a second degree polynomial.

So, zeroes of a second degree polynomial can be found using the formula $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.$

  $\begin{array}{l}\Rightarrow x=\frac{-(8)\pm \sqrt{{(8)}^2-4(1)(17)}}{2(1)}\\ \Rightarrow x=\frac{-8\pm \sqrt{64-68}}{2}\\ \Rightarrow x=\frac{-8\pm \sqrt{-4}}{2}\\ \Rightarrow x=\frac{-8\pm 2\sqrt{-1}}{2}\\ \Rightarrow x=-4\pm i\\ \Rightarrow x=-4+i,-4-i\end{array}$

Conclusion:

Therefore, the zeros of given polynomial function are $x=-2,-4+i\text{and}-4-i.$

b.

To determine

Write the zeros of polynomial $f(x)=x^3+10x^2+33x+34$ as a product of linear factors.

Answer to Problem 44E

  $f(x)=\left(x+2\right)\left(x-(-4+i)\right)\left(x-(-4-i)\right)$

Explanation of Solution

Given:

Function: $f(x)=x^3+10x^2+33x+34$

Calculation:

From above answer, the zeros of given function are $x=-2,-4+i\text{and}-4-i.$

Now, writing the given function as product of linear factors,

  $\Rightarrow f(x)=\left(x+2\right)\left(x-(-4+i)\right)\left(x-(-4-i)\right)$

c.

To determine

Determine the x-intercepts of polynomial $f(x)=x^3+10x^2+33x+34$ using factorization and verify whether the real zeros are the only x-intercepts.

Answer to Problem 44E

1

Explanation of Solution

Given:

Function: $f(x)=x^3+10x^2+33x+34$

Calculation:

Factorization of given function is $f(x)=\left(x+2\right)\left(x-(-4+i)\right)\left(x-(-4-i)\right).$

To find x-intercepts, put $f(x)=0.$

  $\begin{array}{l}\Rightarrow \left(x+2\right)\left(x-(-4+i)\right)\left(x-(-4-i)\right)=0\\ \\ \begin{array}{ccc}\begin{array}{l}\Rightarrow x+2=0\\ \Rightarrow x=-2\end{array}& \begin{array}{l}\Rightarrow x-(-4+i)=0\\ \Rightarrow x=-4+i\end{array}& \begin{array}{l}\Rightarrow x-(-4-i)=0\\ \Rightarrow x=-4-i\end{array}\end{array}\\ \\ \Rightarrow x=-2,-4+i,-4-i\end{array}$

Hence, the x-intercepts are $x=-2,-4+i\text{and}-4-i.$

Calculation for graph:

Consider $f(x)=x^3+10x^2+33x+34$

Values of x	Values of f (x)
0	34
1	78
-1	10
2	148
-2	0

By taking different values of x, the graph can be plotted.

Graph: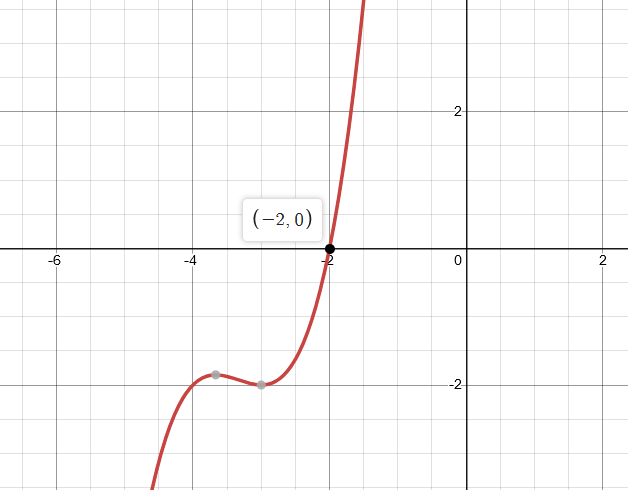

Interpretation:

From graph, it is clear that, the number of x-intercepts is equal to 1.

The number of real zeros of the function is equal to 1.

So, the number of real zeros and number of x-intercepts are equal to each other.