Chapter 1.5, Problem 80E

(a)

To determine

To create a table showing the values of $y_1$ , $y_2$ and $y_3$ from the year 2006 to 2016 using the given mathematical model.

Answer to Problem 80E

The model fits the data well.

Explanation of Solution

Given information:

The given data is approximated by the three mathematical models, where t represents the year, with corresponding to 2006

  $y_1=0.19t^2+2.9t+255$

  $y_2=2.55t^2+37.4t+1224$

  $y_3=0.31t^2+1.0t+163$

Calculation:

The values of $y_1$ , $y_2$ and $y_3$ from the year 2006 to 2016 is calculated using the mathematical model as given below:

For the year 2006 ( $t=6$)

  $y_1=0.19{\left(6\right)}^2+2.9\left(6\right)+255=279.24$

  $y_2=2.55{\left(6\right)}^2+37.4\left(6\right)+1224=1540.2$

  $y_3=0.31{\left(6\right)}^2+1.0\left(6\right)+163\text{ =180}\text{.16}$

For the year 2007 ( $t=7$)

  $y_1=0.19{\left(7\right)}^2+2.9\left(7\right)+255=284.61$

  $y_2=2.55{\left(7\right)}^2+37.4\left(7\right)+1224=1610.75$

  $y_3=0.31{\left(7\right)}^2+1.0\left(7\right)+163\text{ =185}\text{.68}$

For the year 2008 ( $t=8$)

  $y_1=0.19{\left(8\right)}^2+2.9\left(8\right)+255=290.36$

  $y_2=2.55{\left(8\right)}^2+37.4\left(8\right)+1224=1686.4$

  $y_3=0.31{\left(8\right)}^2+1.0\left(8\right)+163\text{ =190}\text{.84}$

For the year 2009( $t=9$)

  $y_1=0.19{\left(9\right)}^2+2.9\left(9\right)+255=296.49$

  $y_2=2.55{\left(9\right)}^2+37.4\left(9\right)+1224=1767.15$

  $y_3=0.31{\left(9\right)}^2+1.0\left(9\right)+163\text{ =197}\text{.11}$

Similarly the values of $y_1$ , $y_2$ and $y_3$ for the next years are calculated and formulated in a table as:

Year	$y_1$	$y_2$	$y_3$
2006	279.24	1540.2	180.16
2007	284.61	1610.75	185.16
2008	290.36	1686.4	190.84
2009	296.49	1767.15	197.11
2010	303	1853	204
2011	309.89	1943.95	199.11
2012	317.16	2040	219.64
2013	324.81	2141.15	228.39
2014	332.84	2247.4	237.76
2015	341.25	2358.75	247.75
2016	350.04	2475.2	258.36

The given mathematical model is a good fit because they predict the actual data points almost accurately.

(b)

To determine

To graph $y_1$ , $y_2$ , $y_3$ and $y_T$

Answer to Problem 80E

The function $y_T$ represent the overall health expenditure in US in each year.

Explanation of Solution

Given information:

Year	$y_1$	$y_2$	$y_3$	$y_T$
2006	273	1517	179	1969
2007	290	1609	192	2091
2008	295	1696	188	4270
2009	294	1796	192	2282
2010	300	1877	204	2381
2011	310	1950	205	2465
2012	318	2023	225	2566
2013	325	2088	235	2648
2014	330	2228	239	2797
2015	339	2383	243	2965
2016	353	2487	258	3098

Graph:

The graph of $y_1$ , $y_2$ , $y_3$ and $y_T$$=y_1+y_2+y_3$ is sketched below:

  

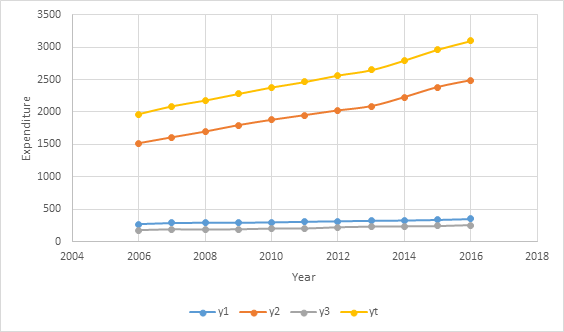
Interpretation: The function $y_T$ represent the overall health expenditure in US in each year.