Chapter 1.6, Problem 27E

a.

To determine

To show : that $f\text{ and }g$ are the inverse functions algebraically.

Explanation of Solution

Given information :

The functionsare $f\left(x\right)=-\sqrt{x-8}$ and $g\left(x\right)=8+x^2$

Prove : if $f\text{ and }g$ are the inverse functions then, they must verify $f(g(x))=x$.

Now, substitute the x of function f by function $g(x)$ ,

  $\begin{array}{l}f(g(x))=x\\ f\left(8+x^2\right)=x\text{ [}g\left(x\right)=8+x^2]\\ -\sqrt{8+x^2-8}=x\text{ [}f\left(x\right)=-\sqrt{x-8}]\\ -\sqrt{x^2}=x\text{ [simplify]}\\ x=x\text{ [simplify]}\end{array}$

Thus, the functions are inverse function.

b.

To determine

To show : that $f\text{ and }g$ are the inverse functions graphically.

Explanation of Solution

Given information :

The functions are $f\left(x\right)=-\sqrt{x-8}$ and $g\left(x\right)=8+x^2$

Prove : by using graphing utility, enter $y_1=f\left(x\right)$ and $y_2=g\left(x\right)$

x	$y_1$	$y_2$
12	2	152
17	3	297
24	4	584
33	5	1097

By using these points and table, the graph can be obtained as:

  

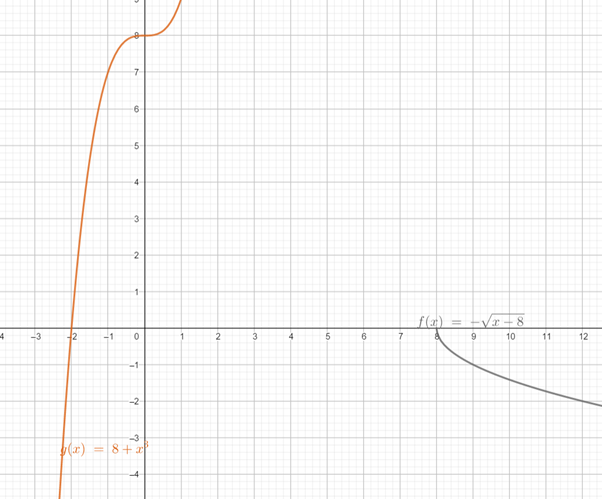
Form the above graph it can be observed that the graph of both function is reflection in the line $y=x$.

Thus, the functions are inverse function.

c.

To determine

To show : that $f\text{ and }g$ are the inverse functions numerically.

Explanation of Solution

Given information :

The functions are $f\left(x\right)=-\sqrt{x-8}$ and $g\left(x\right)=8+x^2$

Prove : to show the functions are inverse function numerically, by using a graphing utility.

Enter $y_1=f\left(x\right)$ , $y_2=g\left(x\right)$ , $y_3=f\left(g\left(x\right)\right)$ ,and $y_4=g\left(f\left(x\right)\right)$

$x$	$y_3$	$y_4$
8	8	8
9	9	9
10	10	10
11	11	11
12	12	12

From the table it can be observed that the entries for x , $y_3$ and $y_4$ are the same. So, it appears that $f\left(g\left(x\right)\right)=x$ and $g\left(f\left(x\right)\right)=x$.

Thus, the functions are inverse function.