PRECALCULUS W/LIMITS:GRAPH.APPROACH(HS)
PRECALCULUS W/LIMITS:GRAPH.APPROACH(HS)
8th Edition
ISBN: 9781337904285
Author: Larson
Publisher: CENGAGE L
bartleby

Concept explainers

Family of Curves
A family of curves is a group of curves that are each described by a parametrization in which one or more variables are parameters. In general, the parameters have more complexity on the assembly of the curve than an ordinary linear transformation. These…
XZ Plane
In order to understand XZ plane, it's helpful to understand two-dimensional and three-dimensional spaces. To plot a point on a plane, two numbers are needed, and these two numbers in the plane can be represented as an ordered pair (a,b) where a and b are…
Euclidean Geometry
Geometry is the branch of mathematics that deals with flat surfaces like lines, angles, points, two-dimensional figures, etc. In Euclidean geometry, one studies the geometrical shapes that rely on different theorems and axioms. This (pure mathematics) ge…
Lines and Angles
In a two-dimensional plane, a line is simply a figure that joins two points. Usually, lines are used for presenting objects that are straight in shape and have minimal depth or width.
bartleby

Videos

Question
Book Icon
Chapter 1.1, Problem 83E
To determine

Calculate the slope − intersept form of the equation of line y 2 .

Expert Solution & Answer
Check Mark

Answer to Problem 83E

The slope − intersept form of the equation of line is y2=−12x+1 .

Explanation of Solution

Given:

It is given in the question that the lines are perpendicular and the graph is given below.

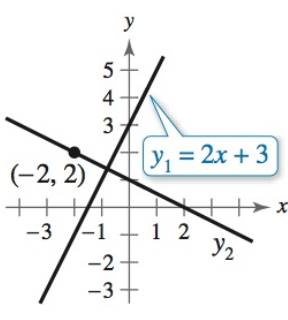
  PRECALCULUS W/LIMITS:GRAPH.APPROACH(HS), Chapter 1.1, Problem 83E

Concept Used:

In this,use the concept that all the perpendicular lines lines have slopes that are the negative reciprocals and the slope intersept form y=mx+c .

Calculation:

In this,it is known that the perpendicular lines lines have slopes that are the negative reciprocals.

Now,the equation of the first line is y1=2x+3 .Also a point is given i.e, (−2,2) .

So,the slope of this perpendicular line is 2 ,so,the slope of this another line will be −12 .

From the graph it is clearly seen that y 2 crosses the y −axis at 1 .

So,the equation of the line y 2 , y2=−12x+1 .

Conclusion:

The equation of line is y2=−12x+1 .

Previous
Chapter 1.1, Problem 82E
Next
Chapter 1.1, Problem 84E

Chapter 1 Solutions

PRECALCULUS W/LIMITS:GRAPH.APPROACH(HS)

Ch. 1.1 - Prob. 1ECh. 1.1 - Prob. 2ECh. 1.1 - Prob. 3ECh. 1.1 - Prob. 4ECh. 1.1 - Prob. 5ECh. 1.1 - Prob. 6ECh. 1.1 - Prob. 7ECh. 1.1 - Prob. 8ECh. 1.1 - Prob. 9ECh. 1.1 - Prob. 10E
Ch. 1.1 - Prob. 11ECh. 1.1 - Prob. 12ECh. 1.1 - Prob. 13ECh. 1.1 - Prob. 14ECh. 1.1 - Prob. 15ECh. 1.1 - Prob. 16ECh. 1.1 - Prob. 17ECh. 1.1 - Prob. 18ECh. 1.1 - Prob. 19ECh. 1.1 - Prob. 20ECh. 1.1 - Prob. 21ECh. 1.1 - Prob. 22ECh. 1.1 - Prob. 23ECh. 1.1 - Prob. 24ECh. 1.1 - Prob. 25ECh. 1.1 - Prob. 26ECh. 1.1 - Prob. 27ECh. 1.1 - Prob. 28ECh. 1.1 - Prob. 29ECh. 1.1 - Prob. 30ECh. 1.1 - Prob. 31ECh. 1.1 - Prob. 32ECh. 1.1 - Prob. 33ECh. 1.1 - Prob. 34ECh. 1.1 - Prob. 35ECh. 1.1 - Prob. 36ECh. 1.1 - Prob. 37ECh. 1.1 - Prob. 38ECh. 1.1 - Prob. 39ECh. 1.1 - Prob. 40ECh. 1.1 - Prob. 41ECh. 1.1 - Prob. 42ECh. 1.1 - Prob. 43ECh. 1.1 - Prob. 44ECh. 1.1 - Prob. 45ECh. 1.1 - Prob. 46ECh. 1.1 - Prob. 47ECh. 1.1 - Prob. 48ECh. 1.1 - Prob. 49ECh. 1.1 - Prob. 50ECh. 1.1 - Prob. 51ECh. 1.1 - Prob. 52ECh. 1.1 - Prob. 53ECh. 1.1 - Prob. 54ECh. 1.1 - Prob. 55ECh. 1.1 - Prob. 56ECh. 1.1 - Prob. 57ECh. 1.1 - Prob. 58ECh. 1.1 - Prob. 59ECh. 1.1 - Prob. 60ECh. 1.1 - Prob. 61ECh. 1.1 - Prob. 62ECh. 1.1 - Prob. 63ECh. 1.1 - Prob. 64ECh. 1.1 - Prob. 65ECh. 1.1 - Prob. 66ECh. 1.1 - Prob. 67ECh. 1.1 - Prob. 68ECh. 1.1 - Prob. 69ECh. 1.1 - Prob. 70ECh. 1.1 - Prob. 71ECh. 1.1 - Prob. 72ECh. 1.1 - Prob. 73ECh. 1.1 - Prob. 74ECh. 1.1 - Prob. 75ECh. 1.1 - Prob. 76ECh. 1.1 - Prob. 77ECh. 1.1 - Prob. 78ECh. 1.1 - Prob. 79ECh. 1.1 - Prob. 80ECh. 1.1 - Prob. 81ECh. 1.1 - Prob. 82ECh. 1.1 - Prob. 83ECh. 1.1 - Prob. 84ECh. 1.1 - Prob. 85ECh. 1.1 - Prob. 86ECh. 1.1 - Prob. 87ECh. 1.1 - Prob. 88ECh. 1.1 - Prob. 89ECh. 1.1 - Prob. 90ECh. 1.1 - Prob. 91ECh. 1.1 - Prob. 92ECh. 1.1 - Prob. 93ECh. 1.1 - Prob. 94ECh. 1.1 - Prob. 95ECh. 1.1 - Prob. 96ECh. 1.1 - Prob. 97ECh. 1.1 - Prob. 98ECh. 1.1 - Prob. 99ECh. 1.1 - Prob. 100ECh. 1.1 - Prob. 101ECh. 1.1 - Prob. 102ECh. 1.1 - Prob. 103ECh. 1.1 - Prob. 104ECh. 1.1 - Prob. 105ECh. 1.1 - Prob. 106ECh. 1.1 - Prob. 107ECh. 1.1 - Prob. 108ECh. 1.1 - Prob. 109ECh. 1.1 - Prob. 110ECh. 1.1 - Prob. 111ECh. 1.1 - Prob. 112ECh. 1.1 - Prob. 113ECh. 1.1 - Prob. 114ECh. 1.1 - Prob. 115ECh. 1.1 - Prob. 116ECh. 1.1 - Prob. 117ECh. 1.1 - Prob. 118ECh. 1.1 - Prob. 119ECh. 1.1 - Prob. 120ECh. 1.1 - Prob. 121ECh. 1.1 - Prob. 122ECh. 1.1 - Prob. 123ECh. 1.1 - Prob. 124ECh. 1.1 - Prob. 125ECh. 1.1 - Prob. 126ECh. 1.1 - Prob. 127ECh. 1.1 - Prob. 128ECh. 1.1 - Prob. 129ECh. 1.2 - Prob. 1ECh. 1.2 - Prob. 2ECh. 1.2 - Prob. 3ECh. 1.2 - Prob. 4ECh. 1.2 - Prob. 5ECh. 1.2 - Prob. 6ECh. 1.2 - Prob. 7ECh. 1.2 - Prob. 8ECh. 1.2 - Prob. 9ECh. 1.2 - Prob. 10ECh. 1.2 - Prob. 11ECh. 1.2 - Prob. 12ECh. 1.2 - Prob. 13ECh. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Prob. 16ECh. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Prob. 19ECh. 1.2 - Prob. 20ECh. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - Prob. 23ECh. 1.2 - Prob. 24ECh. 1.2 - Prob. 25ECh. 1.2 - Prob. 26ECh. 1.2 - Prob. 27ECh. 1.2 - Prob. 28ECh. 1.2 - Prob. 29ECh. 1.2 - Prob. 30ECh. 1.2 - Prob. 31ECh. 1.2 - Prob. 32ECh. 1.2 - Prob. 33ECh. 1.2 - Prob. 34ECh. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Prob. 37ECh. 1.2 - Prob. 38ECh. 1.2 - Prob. 39ECh. 1.2 - Prob. 40ECh. 1.2 - Prob. 41ECh. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Prob. 51ECh. 1.2 - Prob. 52ECh. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - Prob. 65ECh. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - Prob. 72ECh. 1.2 - Prob. 73ECh. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.2 - Prob. 81ECh. 1.2 - Prob. 82ECh. 1.2 - Prob. 83ECh. 1.2 - Prob. 84ECh. 1.2 - Prob. 85ECh. 1.2 - Prob. 86ECh. 1.2 - Prob. 87ECh. 1.2 - Prob. 88ECh. 1.2 - Prob. 89ECh. 1.2 - Prob. 90ECh. 1.2 - Prob. 91ECh. 1.2 - Prob. 92ECh. 1.2 - Prob. 93ECh. 1.2 - Prob. 94ECh. 1.2 - Prob. 95ECh. 1.2 - Prob. 96ECh. 1.2 - Prob. 97ECh. 1.2 - Prob. 98ECh. 1.3 - Prob. 1ECh. 1.3 - Prob. 2ECh. 1.3 - Prob. 3ECh. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Prob. 7ECh. 1.3 - Prob. 8ECh. 1.3 - Prob. 9ECh. 1.3 - Prob. 10ECh. 1.3 - Prob. 11ECh. 1.3 - Prob. 12ECh. 1.3 - Prob. 13ECh. 1.3 - Prob. 14ECh. 1.3 - Prob. 15ECh. 1.3 - Prob. 16ECh. 1.3 - Prob. 17ECh. 1.3 - Prob. 18ECh. 1.3 - Prob. 19ECh. 1.3 - Prob. 20ECh. 1.3 - Prob. 21ECh. 1.3 - Prob. 22ECh. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - Prob. 25ECh. 1.3 - Prob. 26ECh. 1.3 - Prob. 27ECh. 1.3 - Prob. 28ECh. 1.3 - Prob. 29ECh. 1.3 - Prob. 30ECh. 1.3 - Prob. 31ECh. 1.3 - Prob. 32ECh. 1.3 - Prob. 33ECh. 1.3 - Prob. 34ECh. 1.3 - Prob. 35ECh. 1.3 - Prob. 36ECh. 1.3 - Prob. 37ECh. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - Prob. 47ECh. 1.3 - Prob. 48ECh. 1.3 - Prob. 49ECh. 1.3 - Prob. 50ECh. 1.3 - Prob. 51ECh. 1.3 - Prob. 52ECh. 1.3 - Prob. 53ECh. 1.3 - Prob. 54ECh. 1.3 - Prob. 55ECh. 1.3 - Prob. 56ECh. 1.3 - Prob. 57ECh. 1.3 - Prob. 58ECh. 1.3 - Prob. 59ECh. 1.3 - Prob. 60ECh. 1.3 - Prob. 61ECh. 1.3 - Prob. 62ECh. 1.3 - Prob. 63ECh. 1.3 - Prob. 64ECh. 1.3 - Prob. 65ECh. 1.3 - Prob. 66ECh. 1.3 - Prob. 67ECh. 1.3 - Prob. 68ECh. 1.3 - Prob. 69ECh. 1.3 - Prob. 70ECh. 1.3 - Prob. 71ECh. 1.3 - Prob. 72ECh. 1.3 - Prob. 73ECh. 1.3 - Prob. 74ECh. 1.3 - Prob. 75ECh. 1.3 - Prob. 76ECh. 1.3 - Prob. 77ECh. 1.3 - Prob. 78ECh. 1.3 - Prob. 79ECh. 1.3 - Prob. 80ECh. 1.3 - Prob. 81ECh. 1.3 - Prob. 82ECh. 1.3 - Prob. 83ECh. 1.3 - Prob. 84ECh. 1.3 - Prob. 85ECh. 1.3 - Prob. 86ECh. 1.3 - Prob. 87ECh. 1.3 - Prob. 88ECh. 1.3 - Prob. 89ECh. 1.3 - Prob. 90ECh. 1.3 - Prob. 91ECh. 1.3 - Prob. 92ECh. 1.3 - Prob. 93ECh. 1.3 - Prob. 94ECh. 1.3 - Prob. 95ECh. 1.3 - Prob. 96ECh. 1.3 - Prob. 97ECh. 1.3 - Prob. 98ECh. 1.3 - Prob. 99ECh. 1.3 - Prob. 100ECh. 1.3 - Prob. 101ECh. 1.3 - Prob. 102ECh. 1.3 - Prob. 103ECh. 1.3 - Prob. 104ECh. 1.3 - Prob. 105ECh. 1.3 - Prob. 106ECh. 1.3 - Prob. 107ECh. 1.3 - Prob. 108ECh. 1.3 - Prob. 109ECh. 1.3 - Prob. 110ECh. 1.3 - Prob. 111ECh. 1.3 - Prob. 112ECh. 1.3 - Prob. 113ECh. 1.3 - Prob. 114ECh. 1.3 - Prob. 115ECh. 1.3 - Prob. 116ECh. 1.3 - Prob. 117ECh. 1.3 - Prob. 118ECh. 1.3 - Prob. 119ECh. 1.3 - Prob. 120ECh. 1.3 - Prob. 121ECh. 1.3 - Prob. 122ECh. 1.4 - Prob. 1ECh. 1.4 - Prob. 2ECh. 1.4 - Prob. 3ECh. 1.4 - Prob. 4ECh. 1.4 - Prob. 5ECh. 1.4 - Prob. 6ECh. 1.4 - Prob. 7ECh. 1.4 - Prob. 8ECh. 1.4 - Prob. 9ECh. 1.4 - Prob. 10ECh. 1.4 - Prob. 11ECh. 1.4 - Prob. 12ECh. 1.4 - Prob. 13ECh. 1.4 - Prob. 14ECh. 1.4 - Prob. 15ECh. 1.4 - Prob. 16ECh. 1.4 - Prob. 17ECh. 1.4 - Prob. 18ECh. 1.4 - Prob. 19ECh. 1.4 - Prob. 20ECh. 1.4 - Prob. 21ECh. 1.4 - Prob. 22ECh. 1.4 - Prob. 23ECh. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Prob. 26ECh. 1.4 - Prob. 27ECh. 1.4 - Prob. 28ECh. 1.4 - Prob. 29ECh. 1.4 - Prob. 30ECh. 1.4 - Prob. 31ECh. 1.4 - Prob. 32ECh. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - Prob. 35ECh. 1.4 - Prob. 36ECh. 1.4 - Prob. 37ECh. 1.4 - Prob. 38ECh. 1.4 - Prob. 39ECh. 1.4 - Prob. 40ECh. 1.4 - Prob. 41ECh. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.4 - Prob. 56ECh. 1.4 - Prob. 57ECh. 1.4 - Prob. 58ECh. 1.4 - Prob. 59ECh. 1.4 - Prob. 60ECh. 1.4 - Prob. 61ECh. 1.4 - Prob. 62ECh. 1.4 - Prob. 63ECh. 1.4 - Prob. 64ECh. 1.4 - Prob. 65ECh. 1.4 - Prob. 66ECh. 1.4 - Prob. 67ECh. 1.4 - Prob. 68ECh. 1.4 - Prob. 69ECh. 1.4 - Prob. 70ECh. 1.4 - Prob. 71ECh. 1.4 - Prob. 72ECh. 1.4 - Prob. 73ECh. 1.4 - Prob. 74ECh. 1.4 - Prob. 75ECh. 1.4 - Prob. 76ECh. 1.4 - Prob. 77ECh. 1.4 - Prob. 78ECh. 1.4 - Prob. 79ECh. 1.4 - Prob. 80ECh. 1.4 - Prob. 81ECh. 1.4 - Prob. 82ECh. 1.4 - Prob. 83ECh. 1.4 - Prob. 84ECh. 1.5 - Prob. 1ECh. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Prob. 4ECh. 1.5 - Prob. 5ECh. 1.5 - Prob. 6ECh. 1.5 - Prob. 7ECh. 1.5 - Prob. 8ECh. 1.5 - Prob. 9ECh. 1.5 - Prob. 10ECh. 1.5 - Prob. 11ECh. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - Prob. 14ECh. 1.5 - Prob. 15ECh. 1.5 - Prob. 16ECh. 1.5 - Prob. 17ECh. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Prob. 21ECh. 1.5 - Prob. 22ECh. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Prob. 29ECh. 1.5 - Prob. 30ECh. 1.5 - Prob. 31ECh. 1.5 - Prob. 32ECh. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Prob. 37ECh. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Prob. 40ECh. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Prob. 44ECh. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.5 - Prob. 52ECh. 1.5 - Prob. 53ECh. 1.5 - Prob. 54ECh. 1.5 - Prob. 55ECh. 1.5 - Prob. 56ECh. 1.5 - Prob. 57ECh. 1.5 - Prob. 58ECh. 1.5 - Prob. 59ECh. 1.5 - Prob. 60ECh. 1.5 - Prob. 61ECh. 1.5 - Prob. 62ECh. 1.5 - Prob. 63ECh. 1.5 - Prob. 64ECh. 1.5 - Prob. 65ECh. 1.5 - Prob. 66ECh. 1.5 - Prob. 67ECh. 1.5 - Prob. 68ECh. 1.5 - Prob. 69ECh. 1.5 - Prob. 70ECh. 1.5 - Prob. 71ECh. 1.5 - Prob. 72ECh. 1.5 - Prob. 73ECh. 1.5 - Prob. 74ECh. 1.5 - Prob. 75ECh. 1.5 - Prob. 76ECh. 1.5 - Prob. 77ECh. 1.5 - Prob. 78ECh. 1.5 - Prob. 79ECh. 1.5 - Prob. 80ECh. 1.5 - Prob. 81ECh. 1.5 - Prob. 82ECh. 1.5 - Prob. 83ECh. 1.5 - Prob. 84ECh. 1.5 - Prob. 85ECh. 1.5 - Prob. 86ECh. 1.5 - Prob. 87ECh. 1.5 - Prob. 88ECh. 1.5 - Prob. 89ECh. 1.5 - Prob. 90ECh. 1.5 - Prob. 91ECh. 1.5 - Prob. 92ECh. 1.5 - Prob. 93ECh. 1.5 - Prob. 94ECh. 1.5 - Prob. 95ECh. 1.5 - Prob. 96ECh. 1.5 - Prob. 97ECh. 1.5 - Prob. 98ECh. 1.5 - Prob. 99ECh. 1.5 - Prob. 100ECh. 1.5 - Prob. 101ECh. 1.5 - Prob. 102ECh. 1.6 - Prob. 1ECh. 1.6 - Prob. 2ECh. 1.6 - Prob. 3ECh. 1.6 - Prob. 4ECh. 1.6 - Prob. 5ECh. 1.6 - Prob. 6ECh. 1.6 - Prob. 7ECh. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - Prob. 11ECh. 1.6 - Prob. 12ECh. 1.6 - Prob. 13ECh. 1.6 - Prob. 14ECh. 1.6 - Prob. 15ECh. 1.6 - Prob. 16ECh. 1.6 - Prob. 17ECh. 1.6 - Prob. 18ECh. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prob. 23ECh. 1.6 - Prob. 24ECh. 1.6 - Prob. 25ECh. 1.6 - Prob. 26ECh. 1.6 - Prob. 27ECh. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.6 - Prob. 31ECh. 1.6 - Prob. 32ECh. 1.6 - Prob. 33ECh. 1.6 - Prob. 34ECh. 1.6 - Prob. 35ECh. 1.6 - Prob. 36ECh. 1.6 - Prob. 37ECh. 1.6 - Prob. 38ECh. 1.6 - Prob. 39ECh. 1.6 - Prob. 40ECh. 1.6 - Prob. 41ECh. 1.6 - Prob. 42ECh. 1.6 - Prob. 43ECh. 1.6 - Prob. 44ECh. 1.6 - Prob. 45ECh. 1.6 - Prob. 46ECh. 1.6 - Prob. 47ECh. 1.6 - Prob. 48ECh. 1.6 - Prob. 49ECh. 1.6 - Prob. 50ECh. 1.6 - Prob. 51ECh. 1.6 - Prob. 52ECh. 1.6 - Prob. 53ECh. 1.6 - Prob. 54ECh. 1.6 - Prob. 55ECh. 1.6 - Prob. 56ECh. 1.6 - Prob. 57ECh. 1.6 - Prob. 58ECh. 1.6 - Prob. 59ECh. 1.6 - Prob. 60ECh. 1.6 - Prob. 61ECh. 1.6 - Prob. 62ECh. 1.6 - Prob. 63ECh. 1.6 - Prob. 64ECh. 1.6 - Prob. 65ECh. 1.6 - Prob. 66ECh. 1.6 - Prob. 67ECh. 1.6 - Prob. 68ECh. 1.6 - Prob. 69ECh. 1.6 - Prob. 70ECh. 1.6 - Prob. 71ECh. 1.6 - Prob. 72ECh. 1.6 - Prob. 73ECh. 1.6 - Prob. 74ECh. 1.6 - Prob. 75ECh. 1.6 - Prob. 76ECh. 1.6 - Prob. 77ECh. 1.6 - Prob. 78ECh. 1.6 - Prob. 79ECh. 1.6 - Prob. 80ECh. 1.6 - Prob. 81ECh. 1.6 - Prob. 82ECh. 1.6 - Prob. 83ECh. 1.6 - Prob. 84ECh. 1.6 - Prob. 85ECh. 1.6 - Prob. 86ECh. 1.6 - Prob. 87ECh. 1.6 - Prob. 88ECh. 1.6 - Prob. 89ECh. 1.6 - Prob. 90ECh. 1.6 - Prob. 91ECh. 1.6 - Prob. 92ECh. 1.6 - Prob. 93ECh. 1.6 - Prob. 94ECh. 1.6 - Prob. 95ECh. 1.6 - Prob. 96ECh. 1.6 - Prob. 97ECh. 1.6 - Prob. 98ECh. 1.6 - Prob. 99ECh. 1.6 - Prob. 100ECh. 1.6 - Prob. 101ECh. 1.6 - Prob. 102ECh. 1.6 - Prob. 103ECh. 1.6 - Prob. 104ECh. 1.6 - Prob. 105ECh. 1.6 - Prob. 106ECh. 1.6 - Prob. 107ECh. 1.6 - Prob. 108ECh. 1.6 - Prob. 109ECh. 1.6 - Prob. 110ECh. 1.6 - Prob. 111ECh. 1.6 - Prob. 112ECh. 1.6 - Prob. 113ECh. 1.6 - Prob. 114ECh. 1.6 - Prob. 115ECh. 1.6 - Prob. 116ECh. 1.6 - Prob. 117ECh. 1.6 - Prob. 118ECh. 1.6 - Prob. 119ECh. 1.6 - Prob. 120ECh. 1.6 - Prob. 121ECh. 1.6 - Prob. 122ECh. 1.6 - Prob. 123ECh. 1.6 - Prob. 124ECh. 1.6 - Prob. 125ECh. 1.6 - Prob. 126ECh. 1.6 - Prob. 127ECh. 1.6 - Prob. 128ECh. 1.6 - Prob. 129ECh. 1.6 - Prob. 130ECh. 1.6 - Prob. 131ECh. 1.6 - Prob. 132ECh. 1.6 - Prob. 133ECh. 1.6 - Prob. 134ECh. 1.6 - Prob. 135ECh. 1.6 - Prob. 136ECh. 1.6 - Prob. 137ECh. 1.6 - Prob. 138ECh. 1.6 - Prob. 139ECh. 1.6 - Prob. 140ECh. 1.6 - Prob. 141ECh. 1.6 - Prob. 142ECh. 1.6 - Prob. 143ECh. 1.6 - Prob. 144ECh. 1.7 - Prob. 1ECh. 1.7 - Prob. 2ECh. 1.7 - Prob. 3ECh. 1.7 - Prob. 4ECh. 1.7 - Prob. 5ECh. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - Prob. 9ECh. 1.7 - Prob. 10ECh. 1.7 - Prob. 11ECh. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - Prob. 14ECh. 1.7 - Prob. 15ECh. 1.7 - Prob. 16ECh. 1.7 - Prob. 17ECh. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - Prob. 25ECh. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - Prob. 33ECh. 1.7 - Prob. 34ECh. 1 - Prob. 1CRCh. 1 - Prob. 2CRCh. 1 - Prob. 3CRCh. 1 - Prob. 4CRCh. 1 - Prob. 5CRCh. 1 - Prob. 6CRCh. 1 - Prob. 7CRCh. 1 - Prob. 8CRCh. 1 - Prob. 9CRCh. 1 - Prob. 10CRCh. 1 - Prob. 11CRCh. 1 - Prob. 12CRCh. 1 - Prob. 13CRCh. 1 - Prob. 14CRCh. 1 - Prob. 15CRCh. 1 - Prob. 16CRCh. 1 - Prob. 17CRCh. 1 - Prob. 18CRCh. 1 - Prob. 19CRCh. 1 - Prob. 20CRCh. 1 - Prob. 21CRCh. 1 - Prob. 22CRCh. 1 - Prob. 23CRCh. 1 - Prob. 24CRCh. 1 - Prob. 25CRCh. 1 - Prob. 26CRCh. 1 - Prob. 27CRCh. 1 - Prob. 28CRCh. 1 - Prob. 29CRCh. 1 - Prob. 30CRCh. 1 - Prob. 31CRCh. 1 - Prob. 32CRCh. 1 - Prob. 33CRCh. 1 - Prob. 34CRCh. 1 - Prob. 35CRCh. 1 - Prob. 36CRCh. 1 - Prob. 37CRCh. 1 - Prob. 38CRCh. 1 - Prob. 39CRCh. 1 - Prob. 40CRCh. 1 - Prob. 41CRCh. 1 - Prob. 42CRCh. 1 - Prob. 43CRCh. 1 - Prob. 44CRCh. 1 - Prob. 45CRCh. 1 - Prob. 46CRCh. 1 - Prob. 47CRCh. 1 - Prob. 48CRCh. 1 - Prob. 49CRCh. 1 - Prob. 50CRCh. 1 - Prob. 51CRCh. 1 - Prob. 52CRCh. 1 - Prob. 53CRCh. 1 - Prob. 54CRCh. 1 - Prob. 55CRCh. 1 - Prob. 56CRCh. 1 - Prob. 57CRCh. 1 - Prob. 58CRCh. 1 - Prob. 59CRCh. 1 - Prob. 60CRCh. 1 - Prob. 61CRCh. 1 - Prob. 62CRCh. 1 - Prob. 63CRCh. 1 - Prob. 64CRCh. 1 - Prob. 65CRCh. 1 - Prob. 66CRCh. 1 - Prob. 67CRCh. 1 - Prob. 68CRCh. 1 - Prob. 69CRCh. 1 - Prob. 70CRCh. 1 - Prob. 71CRCh. 1 - Prob. 72CRCh. 1 - Prob. 73CRCh. 1 - Prob. 74CRCh. 1 - Prob. 75CRCh. 1 - Prob. 76CRCh. 1 - Prob. 77CRCh. 1 - Prob. 78CRCh. 1 - Prob. 79CRCh. 1 - Prob. 80CRCh. 1 - Prob. 81CRCh. 1 - Prob. 82CRCh. 1 - Prob. 83CRCh. 1 - Prob. 84CRCh. 1 - Prob. 85CRCh. 1 - Prob. 86CRCh. 1 - Prob. 87CRCh. 1 - Prob. 88CRCh. 1 - Prob. 89CRCh. 1 - Prob. 90CRCh. 1 - Prob. 91CRCh. 1 - Prob. 92CRCh. 1 - Prob. 93CRCh. 1 - Prob. 94CRCh. 1 - Prob. 95CRCh. 1 - Prob. 96CRCh. 1 - Prob. 97CRCh. 1 - Prob. 98CRCh. 1 - Prob. 99CRCh. 1 - Prob. 100CRCh. 1 - Prob. 101CRCh. 1 - Prob. 102CRCh. 1 - Prob. 103CRCh. 1 - Prob. 104CRCh. 1 - Prob. 105CRCh. 1 - Prob. 106CRCh. 1 - Prob. 107CRCh. 1 - Prob. 108CRCh. 1 - Prob. 109CRCh. 1 - Prob. 110CRCh. 1 - Prob. 1CTCh. 1 - Prob. 2CTCh. 1 - Prob. 3CTCh. 1 - Prob. 4CTCh. 1 - Prob. 5CTCh. 1 - Prob. 6CTCh. 1 - Prob. 7CTCh. 1 - Prob. 8CTCh. 1 - Prob. 9CTCh. 1 - Prob. 10CTCh. 1 - Prob. 11CTCh. 1 - Prob. 12CTCh. 1 - Prob. 13CTCh. 1 - Prob. 14CTCh. 1 - Prob. 15CTCh. 1 - Prob. 16CTCh. 1 - Prob. 17CTCh. 1 - Prob. 18CTCh. 1 - Prob. 19CTCh. 1 - Prob. 20CT
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Points, Lines, Planes, Segments, & Rays - Collinear vs Coplanar Points - Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=dDWjhRfBsKM;License: Standard YouTube License, CC-BY
Naming Points, Lines, and Planes; Author: Florida PASS Program;https://www.youtube.com/watch?v=F-LxiLSSaLg;License: Standard YouTube License, CC-BY