Chapter 1.3, Problem 17E

a.

To determine

To calculate: Domain of the function

Answer to Problem 17E

Domain is $x\in \left(-\infty ,\infty \right)$ .

Explanation of Solution

Given information: A graph is given

  

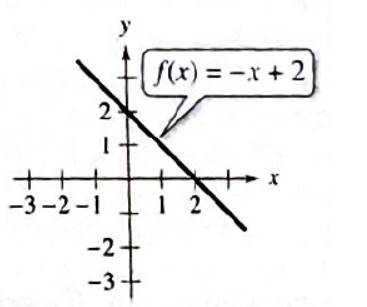
Calculation:

  

Domain of a function refers to a set of all possible input values for that function.

As per the graph, $x\in \left(-\infty ,\infty \right)$

So, domain is $x\in \left(-\infty ,\infty \right)$

b.

To determine

To calculate: Range of the function.

Answer to Problem 17E

Range is $x\in \left(-\infty ,\infty \right)$ .

Explanation of Solution

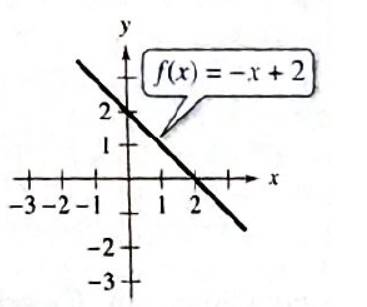
Calculation:

Range of a function refers to a set of all possible output values corresponding to the domain of a function.

  

As per the graph, $f(x)\in \left(-\infty ,\infty \right)$ .

So, range is $\left(-\infty ,\infty \right)$ .

c.

To determine

To calculate: values of $x$ for which $f(x)=0$ .

Answer to Problem 17E

  $f(x)=0$ at $x=2$ .

Explanation of Solution

Calculation:

  

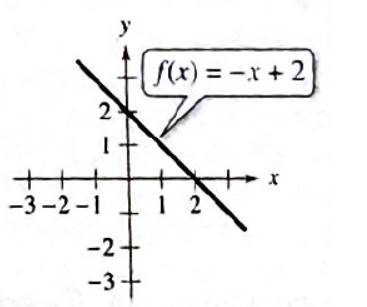
To find values of $x$ for which $f(x)=0$ , find the x -coordinate of the point where the graph cuts the x -axis.

The graph cuts the x -axis at point $(2,0)$ .

x -coordinate of the point $(2,0)$ is $2$ .

So,

  $f(x)=0$ at $x=2$ .

d.

To determine

To calculate: values of $f(0)$ .

Answer to Problem 17E

Value of $f(0)$ is $2$ .

Explanation of Solution

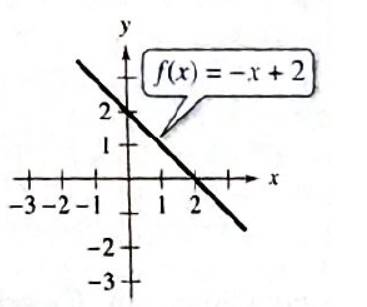
Calculation:

  

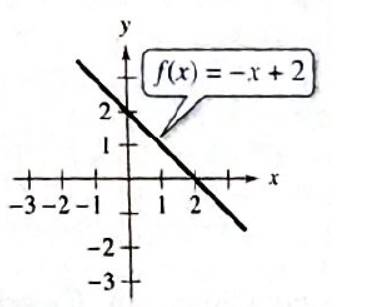
To find $f(0)$ , find the y -coordinate of the point where the graph cuts the y -axis.

The graph cuts the y -axis at point $(0,2)$ .

y-coordinate of the point $(0,2)$ is $2$ .

So,

  $f(0)=2$

e.

To determine

To calculate: values of $f$ at $x=1$ and the corresponding coordinates of the point.

Answer to Problem 17E

Value of $f$ at $x=1$ is $1$ .

Coordinates of the point is $(1,1)$ .

Explanation of Solution

Calculation:

  

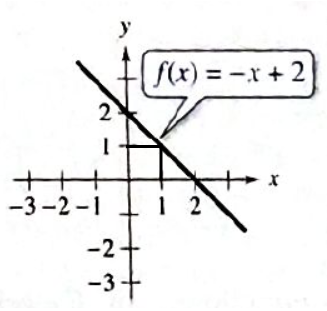
To find value of $f$ at $x=1$ , first draw the vertical line $x=1$ .

The line $x=1$ intersects the graph $f(x)=-x+2$ at some point.

From this point draw a horizontal line which intersects the y -axis at some point.

The horizontal line intersects y -axis at point $(0,1)$ .

y -coordinate of point $(0,1)$ is $1$ .

So,

Value of $f$ at $x=1$ is $1$ .

Coordinates of the point is $(1,f(1))=(1,1)$ .

f.

To determine

To calculate: coordinates of the point on the graph of $f$ at which $x=-3$ .

Answer to Problem 17E

Coordinates of the point on the graph of $f$ at which $x=-3$ are $(-3,f(-3))=(-3,5)$

Explanation of Solution

Calculation:

To find coordinates of the point on the graph of $f$ at which $x=-3$ ,

Put $x=-3$ in $f(x)=-x+2$

  $\begin{array}{c}f(-3)=-(-3)+2\\ =3+2\\ =5\end{array}$

So,

coordinates of the point on the graph of $f$ are $(-3,f(-3))=(-3,5)$ .