Chapter 1.4, Problem 19E

To determine

To sketch the graph of the given functions on same co-ordinate system

Explanation of Solution

Given:

The given functions are:

  $\begin{array}{l}f(x)=\frac{1}{x}\\ g(x)=\frac{1}{x}-2\\ h(x)=\frac{1}{x-1}+2\end{array}$

Calculation for graph:

Consider $f(x)=\frac{1}{x}$

Values of x	Values of f (x )
1	1
2	0.5
3	0.33
4	0.25
5	0.2

By taking different values of x , the graph can be plotted.

Calculation for graph:

Consider $g(x)=\frac{1}{x}-2$

Values of x	Values of g (x)
1	-1
2	-1.5
3	-1.67
4	-1.75
5	-1.8

By taking different values of x , the graph can be plotted.

Calculation for graph:

Consider $h(x)=\frac{1}{x-1}+2$

Values of x	Values of h (x )
2	3
3	2.5
4	2.33
5	2.25
6	2.2

By taking different values of x , the graph can be plotted.

Graphs on the same co-ordinate system:

  

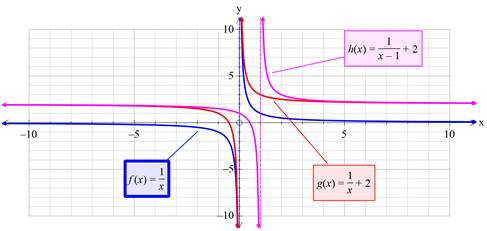
Verification:

Using graphing utility to draw the graph of given functions,

  

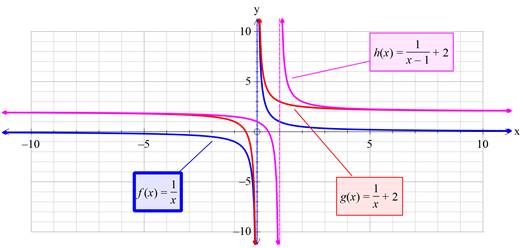
Interpretation:

From above graph, it is clear that, the drawn sketch and above graph are identical to each other.

Here, $f(x)=\frac{1}{x}$ is the base graph.

  $g(x)$ is the rigid transformation of base graph with a vertical shift of 2 units upward..

  $h(x)$ is the rigid transformation of base graph, with horizontal shift of 1 unit to the right and vertical shift of 2 units upward.