Glencoe Math Accelerated, Student Edition
1st Edition
ISBN: 9780076637980
Author: McGraw-Hill Glencoe
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 1.3, Problem 61CCR
To determine
How many more points do the knights have than the panthers.
Expert Solution & Answer
Answer to Problem 61CCR
Explanation of Solution
Given:
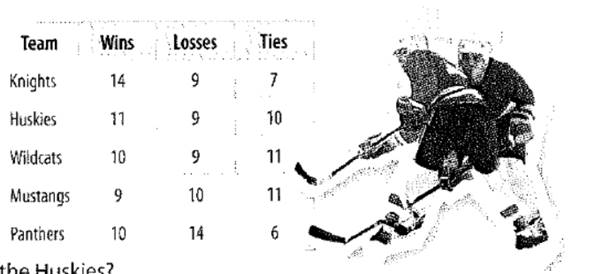
In order to find how many more points do the knights have than the panthers, first calculating knights total points and then calculating panthers total points then subtracting panthers points from knights points so, first knights wins total 14 times so the points for 1 win is 3 points so, the total win points will be calculated by multiplying 14 and 3 and then the knights ties 7 times 1 tie is equal to 1 point so the total points for the ties is calculated by multiplying 1 and 7 now, adding both the wins total points and the ties total points as shown below:
Then panthers wins total 10 times so the points for 1 win is 3 points so, the total win points will be calculated by multiplying 10 and 3 and then the panthers ties 6 times 1 tie is equal to 1 point so the total points for the ties is calculated by multiplying 1 and 6 now, adding both the wins total points and the ties total points as shown below:
Now, subtracting total points of panthers from total points of knights
So, knights have 13 more points than panthers.
Chapter 1 Solutions
Glencoe Math Accelerated, Student Edition
Ch. 1.1 - Prob. 1GPCh. 1.1 - Prob. 2GPCh. 1.1 - Prob. 3GPCh. 1.1 - Prob. 4IPCh. 1.1 - Prob. 5IPCh. 1.1 - Prob. 6IPCh. 1.1 - Prob. 7IPCh. 1.1 - Prob. 8IPCh. 1.1 - Prob. 9HPCh. 1.1 - Prob. 10HP
Ch. 1.1 - Prob. 11HPCh. 1.1 - Prob. 12HPCh. 1.1 - Prob. 13STPCh. 1.1 - Prob. 14STPCh. 1.1 - Prob. 15STPCh. 1.1 - Prob. 16CCRCh. 1.1 - Prob. 17CCRCh. 1.1 - Prob. 18CCRCh. 1.1 - Prob. 19CCRCh. 1.1 - Prob. 20CCRCh. 1.1 - Prob. 21CCRCh. 1.1 - Prob. 22CCRCh. 1.1 - Prob. 23CCRCh. 1.1 - Prob. 24CCRCh. 1.2 - Prob. 1GPCh. 1.2 - Prob. 2GPCh. 1.2 - Prob. 3GPCh. 1.2 - Prob. 4GPCh. 1.2 - Prob. 5GPCh. 1.2 - Prob. 6GPCh. 1.2 - Prob. 7GPCh. 1.2 - Prob. 8GPCh. 1.2 - Prob. 9GPCh. 1.2 - Prob. 10GPCh. 1.2 - Prob. 11GPCh. 1.2 - Prob. 12IPCh. 1.2 - Prob. 13IPCh. 1.2 - Prob. 14IPCh. 1.2 - Prob. 15IPCh. 1.2 - Prob. 16IPCh. 1.2 - Prob. 17IPCh. 1.2 - Prob. 18IPCh. 1.2 - Prob. 19IPCh. 1.2 - Prob. 20IPCh. 1.2 - Prob. 21IPCh. 1.2 - Prob. 22IPCh. 1.2 - Prob. 23IPCh. 1.2 - Prob. 24IPCh. 1.2 - Prob. 25IPCh. 1.2 - Prob. 26IPCh. 1.2 - Prob. 27IPCh. 1.2 - Prob. 28IPCh. 1.2 - Prob. 29IPCh. 1.2 - Prob. 30IPCh. 1.2 - Prob. 31IPCh. 1.2 - Prob. 32IPCh. 1.2 - Prob. 33IPCh. 1.2 - Prob. 34IPCh. 1.2 - Prob. 35HPCh. 1.2 - Prob. 36HPCh. 1.2 - Prob. 37HPCh. 1.2 - Prob. 38STPCh. 1.2 - Prob. 39STPCh. 1.2 - Prob. 40STPCh. 1.2 - Prob. 41STPCh. 1.2 - Prob. 42CCRCh. 1.2 - Prob. 43CCRCh. 1.2 - Prob. 44CCRCh. 1.2 - Prob. 45CCRCh. 1.2 - Prob. 46CCRCh. 1.2 - Prob. 47CCRCh. 1.2 - Prob. 48CCRCh. 1.2 - Prob. 49CCRCh. 1.2 - Prob. 50CCRCh. 1.3 - Prob. 1GPCh. 1.3 - Prob. 2GPCh. 1.3 - Prob. 3GPCh. 1.3 - Prob. 4GPCh. 1.3 - Prob. 5GPCh. 1.3 - Prob. 6GPCh. 1.3 - Prob. 7GPCh. 1.3 - Prob. 8GPCh. 1.3 - Prob. 9GPCh. 1.3 - Prob. 10GPCh. 1.3 - Prob. 11GPCh. 1.3 - Prob. 12IPCh. 1.3 - Prob. 13IPCh. 1.3 - Prob. 14IPCh. 1.3 - Prob. 15IPCh. 1.3 - Prob. 16IPCh. 1.3 - Prob. 17IPCh. 1.3 - Prob. 18IPCh. 1.3 - Prob. 19IPCh. 1.3 - Prob. 20IPCh. 1.3 - Prob. 21IPCh. 1.3 - Prob. 22IPCh. 1.3 - Prob. 23IPCh. 1.3 - Prob. 24IPCh. 1.3 - Prob. 25IPCh. 1.3 - Prob. 26IPCh. 1.3 - Prob. 27IPCh. 1.3 - Prob. 28IPCh. 1.3 - Prob. 29IPCh. 1.3 - Prob. 30IPCh. 1.3 - Prob. 31IPCh. 1.3 - Prob. 32IPCh. 1.3 - Prob. 33IPCh. 1.3 - Prob. 34IPCh. 1.3 - Prob. 35IPCh. 1.3 - Prob. 36IPCh. 1.3 - Prob. 37IPCh. 1.3 - Prob. 38IPCh. 1.3 - Prob. 39IPCh. 1.3 - Prob. 40IPCh. 1.3 - Prob. 41IPCh. 1.3 - Prob. 42HPCh. 1.3 - Prob. 43HPCh. 1.3 - Prob. 44HPCh. 1.3 - Prob. 45HPCh. 1.3 - Prob. 46STPCh. 1.3 - Prob. 47STPCh. 1.3 - Prob. 48STPCh. 1.3 - Prob. 49STPCh. 1.3 - Prob. 50CCRCh. 1.3 - Prob. 51CCRCh. 1.3 - Prob. 52CCRCh. 1.3 - Prob. 53CCRCh. 1.3 - Prob. 54CCRCh. 1.3 - Prob. 55CCRCh. 1.3 - Prob. 56CCRCh. 1.3 - Prob. 57CCRCh. 1.3 - Prob. 58CCRCh. 1.3 - Prob. 59CCRCh. 1.3 - Prob. 60CCRCh. 1.3 - Prob. 61CCRCh. 1.3 - Prob. 62CCRCh. 1.3 - Prob. 63CCRCh. 1.3 - Prob. 64CCRCh. 1.3 - Prob. 65CCRCh. 1.3 - Prob. 66CCRCh. 1.3 - Prob. 67CCRCh. 1.3 - Prob. 68CCRCh. 1.3 - Prob. 69CCRCh. 1.3 - Prob. 70CCRCh. 1.3 - Prob. 71CCRCh. 1.4 - Prob. 1GPCh. 1.4 - Prob. 2GPCh. 1.4 - Prob. 3GPCh. 1.4 - Prob. 4GPCh. 1.4 - Prob. 5GPCh. 1.4 - Prob. 6GPCh. 1.4 - Prob. 7GPCh. 1.4 - Prob. 8GPCh. 1.4 - Prob. 9GPCh. 1.4 - Prob. 10GPCh. 1.4 - Prob. 11GPCh. 1.4 - Prob. 12GPCh. 1.4 - Prob. 13GPCh. 1.4 - Prob. 14GPCh. 1.4 - Prob. 15GPCh. 1.4 - Prob. 16GPCh. 1.4 - Prob. 17GPCh. 1.4 - Prob. 18IPCh. 1.4 - Prob. 19IPCh. 1.4 - Prob. 20IPCh. 1.4 - Prob. 21IPCh. 1.4 - Prob. 22IPCh. 1.4 - Prob. 23IPCh. 1.4 - Prob. 24IPCh. 1.4 - Prob. 25IPCh. 1.4 - Prob. 26IPCh. 1.4 - Prob. 27IPCh. 1.4 - Prob. 28IPCh. 1.4 - Prob. 29IPCh. 1.4 - Prob. 30IPCh. 1.4 - Prob. 31IPCh. 1.4 - Prob. 32IPCh. 1.4 - Prob. 33IPCh. 1.4 - Prob. 34IPCh. 1.4 - Prob. 35IPCh. 1.4 - Prob. 36IPCh. 1.4 - Prob. 37IPCh. 1.4 - Prob. 38IPCh. 1.4 - Prob. 39IPCh. 1.4 - Prob. 40IPCh. 1.4 - Prob. 41IPCh. 1.4 - Prob. 42IPCh. 1.4 - Prob. 43IPCh. 1.4 - Prob. 44IPCh. 1.4 - Prob. 45IPCh. 1.4 - Prob. 46IPCh. 1.4 - Prob. 47IPCh. 1.4 - Prob. 48IPCh. 1.4 - Prob. 49IPCh. 1.4 - Prob. 50HPCh. 1.4 - Prob. 51HPCh. 1.4 - Prob. 52HPCh. 1.4 - Prob. 53HPCh. 1.4 - Prob. 54HPCh. 1.4 - Prob. 55STPCh. 1.4 - Prob. 56STPCh. 1.4 - Prob. 57STPCh. 1.4 - Prob. 58STPCh. 1.4 - Prob. 59CCRCh. 1.4 - Prob. 60CCRCh. 1.4 - Prob. 61CCRCh. 1.4 - Prob. 62CCRCh. 1.4 - Prob. 63CCRCh. 1.4 - Prob. 64CCRCh. 1.4 - Prob. 65CCRCh. 1.4 - Prob. 66CCRCh. 1.4 - Prob. 67CCRCh. 1.4 - Prob. 68CCRCh. 1.4 - Prob. 69CCRCh. 1.4 - Prob. 70CCRCh. 1.4 - Prob. 71CCRCh. 1.4 - Prob. 72CCRCh. 1.4 - Prob. 73CCRCh. 1.4 - Prob. 74CCRCh. 1.4 - Prob. 75CCRCh. 1.4 - Prob. 76CCRCh. 1.4 - Prob. 77CCRCh. 1.4 - Prob. 78CCRCh. 1.4 - Prob. 79CCRCh. 1.4 - Prob. 80CCRCh. 1.5 - Prob. 1GPCh. 1.5 - Prob. 2GPCh. 1.5 - Prob. 3GPCh. 1.5 - Prob. 4GPCh. 1.5 - Prob. 5IPCh. 1.5 - Prob. 6IPCh. 1.5 - Prob. 7IPCh. 1.5 - Prob. 8IPCh. 1.5 - Prob. 9IPCh. 1.5 - Prob. 10IPCh. 1.5 - Prob. 11IPCh. 1.5 - Prob. 12IPCh. 1.5 - Prob. 13IPCh. 1.5 - Prob. 14IPCh. 1.5 - Prob. 15IPCh. 1.5 - Prob. 16HPCh. 1.5 - Prob. 17HPCh. 1.5 - Prob. 18HPCh. 1.5 - Prob. 19HPCh. 1.5 - Prob. 20STPCh. 1.5 - Prob. 21STPCh. 1.5 - Prob. 22STPCh. 1.5 - Prob. 23STPCh. 1.5 - Prob. 24CCRCh. 1.5 - Prob. 25CCRCh. 1.5 - Prob. 26CCRCh. 1.5 - Prob. 27CCRCh. 1.5 - Prob. 28CCRCh. 1.5 - Prob. 29CCRCh. 1.5 - Prob. 30CCRCh. 1.5 - Prob. 31CCRCh. 1.5 - Prob. 32CCRCh. 1.5 - Prob. 33CCRCh. 1.5 - Prob. 34CCRCh. 1.5 - Prob. 35CCRCh. 1.6 - Prob. 1GPCh. 1.6 - Prob. 2GPCh. 1.6 - Prob. 3GPCh. 1.6 - Prob. 4GPCh. 1.6 - Prob. 5GPCh. 1.6 - Prob. 6GPCh. 1.6 - Prob. 7GPCh. 1.6 - Prob. 8GPCh. 1.6 - Prob. 9GPCh. 1.6 - Prob. 10GPCh. 1.6 - Prob. 11GPCh. 1.6 - Prob. 12IPCh. 1.6 - Prob. 13IPCh. 1.6 - Prob. 14IPCh. 1.6 - Prob. 15IPCh. 1.6 - Prob. 16IPCh. 1.6 - Prob. 17IPCh. 1.6 - Prob. 18IPCh. 1.6 - Prob. 19IPCh. 1.6 - Prob. 20IPCh. 1.6 - Prob. 21IPCh. 1.6 - Prob. 22IPCh. 1.6 - Prob. 23IPCh. 1.6 - Prob. 24IPCh. 1.6 - Prob. 25IPCh. 1.6 - Prob. 26IPCh. 1.6 - Prob. 27IPCh. 1.6 - Prob. 28IPCh. 1.6 - Prob. 29IPCh. 1.6 - Prob. 30IPCh. 1.6 - Prob. 31IPCh. 1.6 - Prob. 32IPCh. 1.6 - Prob. 33IPCh. 1.6 - Prob. 34IPCh. 1.6 - Prob. 35IPCh. 1.6 - Prob. 36IPCh. 1.6 - Prob. 37HPCh. 1.6 - Prob. 38HPCh. 1.6 - Prob. 39HPCh. 1.6 - Prob. 40HPCh. 1.6 - Prob. 41STPCh. 1.6 - Prob. 42STPCh. 1.6 - Prob. 43STPCh. 1.6 - Prob. 44STPCh. 1.6 - Prob. 45CCRCh. 1.6 - Prob. 46CCRCh. 1.6 - Prob. 47CCRCh. 1.6 - Prob. 48CCRCh. 1.6 - Prob. 49CCRCh. 1.6 - Prob. 50CCRCh. 1.6 - Prob. 51CCRCh. 1.6 - Prob. 52CCRCh. 1.6 - Prob. 53CCRCh. 1.6 - Prob. 54CCRCh. 1.6 - Prob. 55CCRCh. 1.6 - Prob. 56CCRCh. 1.6 - Prob. 57CCRCh. 1.6 - Prob. 58CCRCh. 1.6 - Prob. 59CCRCh. 1.6 - Prob. 60CCRCh. 1.6 - Prob. 61CCRCh. 1.6 - Prob. 62CCRCh. 1.6 - Prob. 63CCRCh. 1.7 - Prob. 1GPCh. 1.7 - Prob. 2GPCh. 1.7 - Prob. 3GPCh. 1.7 - Prob. 4IPCh. 1.7 - Prob. 5IPCh. 1.7 - Prob. 6IPCh. 1.7 - Prob. 7IPCh. 1.7 - Prob. 8IPCh. 1.7 - Prob. 9IPCh. 1.7 - Prob. 10IPCh. 1.7 - Prob. 11IPCh. 1.7 - Prob. 12HPCh. 1.7 - Prob. 13HPCh. 1.7 - Prob. 14HPCh. 1.7 - Prob. 15HPCh. 1.7 - Prob. 16HPCh. 1.7 - Prob. 17HPCh. 1.7 - Prob. 18HPCh. 1.7 - Prob. 19HPCh. 1.7 - Prob. 20CCRCh. 1.7 - Prob. 21CCRCh. 1.7 - Prob. 22CCRCh. 1.7 - Prob. 23CCRCh. 1.7 - Prob. 24CCRCh. 1.7 - Prob. 25CCRCh. 1.7 - Prob. 26CCRCh. 1.7 - Prob. 27CCRCh. 1.7 - Prob. 28CCRCh. 1.7 - Prob. 29CCRCh. 1.7 - Prob. 30CCRCh. 1.7 - Prob. 31CCRCh. 1.7 - Prob. 32CCRCh. 1.7 - Prob. 33CCRCh. 1.7 - Prob. 34CCRCh. 1.7 - Prob. 35CCRCh. 1.7 - Prob. 36CCRCh. 1.7 - Prob. 37CCRCh. 1.7 - Prob. 38CCRCh. 1.7 - Prob. 39CCRCh. 1.7 - Prob. 40CCRCh. 1.7 - Prob. 41CCRCh. 1.7 - Prob. 42CCRCh. 1.7 - Prob. 43CCRCh. 1.7 - Prob. 44CCRCh. 1 - Prob. 1CRCh. 1 - Prob. 2CRCh. 1 - Prob. 3CRCh. 1 - Prob. 4CRCh. 1 - Prob. 5CRCh. 1 - Prob. 6CRCh. 1 - Prob. 7CRCh. 1 - Prob. 8CRCh. 1 - Prob. 9CRCh. 1 - Prob. 10CRCh. 1 - Prob. 11CRCh. 1 - Prob. 12CRCh. 1 - Prob. 13CRCh. 1 - Prob. 14CRCh. 1 - Prob. 15CRCh. 1 - Prob. 16CRCh. 1 - Prob. 17CRCh. 1 - Prob. 18CRCh. 1 - Prob. 19CRCh. 1 - Prob. 20CRCh. 1 - Prob. 21CRCh. 1 - Prob. 22CRCh. 1 - Prob. 23CRCh. 1 - Prob. 24CRCh. 1 - Prob. 25CRCh. 1 - Prob. 26CRCh. 1 - Prob. 27CRCh. 1 - Prob. 28CRCh. 1 - Prob. 29CRCh. 1 - Prob. 30CRCh. 1 - Prob. 31CRCh. 1 - Prob. 32CRCh. 1 - Prob. 33CRCh. 1 - Prob. 34CRCh. 1 - Prob. 35CRCh. 1 - Prob. 36CRCh. 1 - Prob. 37CRCh. 1 - Prob. 38CRCh. 1 - Prob. 39CRCh. 1 - Prob. 40CRCh. 1 - Prob. 41CR
Additional Math Textbook Solutions
Find more solutions based on key concepts
Siblings The histogram shows the distribution of the numbers of siblings (brothers and sisters) for 2000 adults...
Introductory Statistics
Percentiles. In Exercises 17-20, use the following cell phone airport data speeds (Mbps) from Sprint. Find the ...
Elementary Statistics (13th Edition)
If n is a counting number, bn, read______, indicates that there are n factors of b. The number b is called the_...
Algebra and Trigonometry (6th Edition)
Logarithmic differentiation Use logarithmic differentiation to evaluate f(x). 61. f(x)=(x+1)10(2x4)8
Calculus: Early Transcendentals (2nd Edition)
Using
Find the limits in Exercises 23–46.
25.
University Calculus: Early Transcendentals (4th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 3:59 m s ☑ D'Aniello Boutique | Fashion VOLTE danielloboutique.it/asia SUBSCRIBE NOW: 10% OFF TO USE ANYTIME YOU WANT d'aniello NEW IN WOMEN NEW IN MEN WINTER SALE: 50% OFF on FW24 SHOP WOMEN SHOP MENarrow_forwardJOB UPDATE EMERSON GRAD ENGINEER (FRESHERS) SOFTWARE ENGG NEW RELIC BROWSERSTACK (FRESHERS) SOFTWARE ENGG FULL STACK DATA ENGINEER GENPACT + PYTHON CARS24 WORK FROM HOME #vinkjobs TELE PERFORMANCE Vinkjobs.com CUSTOMER SUPPORT Search "Vinkjobs.com" on Googlearrow_forwarddo question 2 pleasearrow_forward
- question 10 pleasearrow_forward00 (a) Starting with the geometric series Σ X^, find the sum of the series n = 0 00 Σηχη - 1, |x| < 1. n = 1 (b) Find the sum of each of the following series. 00 Σnx", n = 1 |x| < 1 (ii) n = 1 sin (c) Find the sum of each of the following series. (i) 00 Σn(n-1)x^, |x| <1 n = 2 (ii) 00 n = 2 n² - n 4n (iii) M8 n = 1 շոarrow_forward(a) Use differentiation to find a power series representation for 1 f(x) = (4 + x)²* f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (b) Use part (a) to find a power series for f(x) = 1 (4 + x)³° f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (c) Use part (b) to find a power series for f(x) = x² (4 + x)³* 00 f(x) = Σ n = 2 What is the radius of convergence, R? R = Need Help? Read It Watch It SUBMIT ANSWERarrow_forward
- answer for question 4 pleasearrow_forward(3) (20 points) Let F(x, y, z) = (y, z, x²z). Define E = {(x, y, z) | x² + y² ≤ z ≤ 1, x ≤ 0}. (a) (2 points) Calculate the divergence V. F. (b) (4 points) Let D = {(x, y) | x² + y² ≤ 1, x ≤ 0} Without calculation, show that the triple integral √ (V · F) dV = √ 2²(1. = x²(1 − x² - y²) dA. Earrow_forward(2) (22 points) Let F(x, y, z) = (x sin y, cos y, ―xy). (a) (2 points) Calculate V. F. (b) (6 points) Given a vector field is everywhere defined with V G₁(x, y, z) = * G2(x, y, z) = − G3(x, y, z) = 0. 0 0 F(x, y, z) = (F₁(x, y, z), F₂(x, y, z), F(x, y, z)) that F = 0, let G = (G1, G2, G3) where F₂(x, y, y, t) dt - √ F³(x, t, 0) dt, * F1(x, y, t) dt, t) dt - √ F Calculate G for the vector field F(x, y, z) = (x sin y, cos y, -xy).arrow_forward
- Evaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √(x + y) A R R = {(x, y) | 25 < x² + y² ≤ 36, x < 0} Hint: The integral and Region is defined in rectangular coordinates.arrow_forwardFind the volume of the solid that lies under the paraboloid z = 81 - x² - y² and within the cylinder (x − 1)² + y² = 1. A plot of an example of a similar solid is shown below. (Answer accurate to 2 decimal places). Volume using Double Integral Paraboloid & Cylinder -3 Hint: The integral and region is defined in polar coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √4(1–2² 4(1 - x² - y²) dA R 3 R = {(r,0) | 0 ≤ r≤ 2,0π ≤0≤¼˜}. Hint: The integral is defined in rectangular coordinates. The Region is defined in polar coordinates.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY