Chapter 1.4, Problem 49IP

a.

To determine

The algebraic expression for the total cost for five people to get into the center, visit the planetarium, and watch a 3-D movie.

Answer to Problem 49IP

  $5a+61.25$

Explanation of Solution

Given:

The rates for the Center of Wonders science center

  

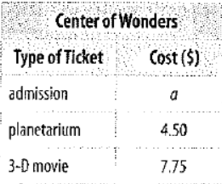
Calculation:

Observe that the cost of admission of person is a , and the cost of visiting the planetarium is $4.50 and the cost of watching a 3-D movie is $7.75. So, the total cost of one person to go into the center, visit the planetarium and watching a 3-D movies is

  $\begin{array}{c}\text{Total cost of 1 person}=a+4.50+7.75\\ =a+12.25\end{array}$

So, the total cost of 5 people can be obtained by multiplying the total cost of 1 person by 5. That is,

  $\begin{array}{c}\text{Total cost for 5 people}=5\left(a+12.25\right)\\ =5a+61.25\end{array}$

Thus, the total cost for 5 people is, $5a+61.25$.

b.

To determine

The cost for four people to get into the center and watch a 3-D movie if the cost of admission to the center is $12.

Answer to Problem 49IP

  $\$79$

Explanation of Solution

Given:

The rates for the Center of Wonders science center

  

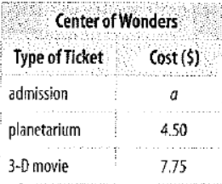
Calculation:

Given that the cost of admission of person is $12, and the cost of visiting the planetarium is $4.50 and the cost of watching a 3-D movie is $7.75. So, the total cost of one person to get into the center, and watching a 3-D movies is

  $\begin{array}{c}\text{Total cost of 1 person}=12+7.75\\ =19.75\end{array}$

So, the total cost of 4 people can be obtained by multiplying the total cost of 1 person by 4. That is,

  $\begin{array}{c}\text{Total cost for 4 people}=4\left(19.75\right)\\ =79\end{array}$

Thus, the total cost for 4 people is, $\$79$.

c.

To determine

The cost for two adults and two children to get into the center, see a 3-D movie and visit the planetarium.

Answer to Problem 49IP

  $4a+44$

Explanation of Solution

Given:

Children get a discount of $2.50 on their tickets to the planetarium if they also watch a 3-D movie. The rates for the Center of Wonders science center

  

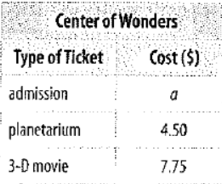
Calculation:

Observe that the cost of admission of person is a , and the cost of visiting the planetarium is $4.50 and the cost of watching a 3-D movie is $7.75. So, the total cost of one adult to go into the center, visit the planetarium and watching a 3-D movies is

  $\begin{array}{c}\text{Total cost of 1 person}=a+4.50+7.75\\ =a+12.25\end{array}$

Since the children get a discount of $2.50 on their tickets to the planetarium if they watch a 3-D movie also. So, the cost of 1 child to get into the center, see a 3-D movie, and visit the planetarium is

  $\begin{array}{c}\text{Total cost of 1 child}=a+\left(4.50-2.50\right)+7.75\\ =a+9.75\end{array}$

So, the total cost for two adults and two children to get into the center, see a 3-D movie, and visit the planetarium is given by

  $\begin{array}{c}\text{Total cost}=2\left(a+12.25\right)+2\left(a+9.75\right)\\ =2a+24.5+2a+19.5\\ =4a+44\end{array}$

Thus, the total cost for two adults and two children is, $4a+44$.