Chapter 12.5, Problem 19PSC

To determine

To calculate: The volume of pyramid with slant height $13$.

Answer to Problem 19PSC

The volume of pyramid is $48$ .

Explanation of Solution

Given information:

Base of pyramid $b=6,$

Slant height $l=13$

Formula used:

The below theorem is used:

Pythagoras theorem states that “In a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”.

  

In right angle triangle,

  $a^2+b^2\text{= }{c}^2$

Volume of pyramid $=\frac{1}{3}B\times x$

B = Base area of pyramid and x = height of pyramid

Area of triangle: $A=\frac{1}{2}\times b\times h$

b = base of triangle

h = height of triangle

Calculation:

  

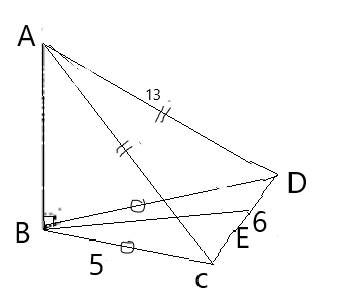
The height AB can be calculated by applying Pythagoras Theorem.

In right angled triangle ABC , we get

  $\begin{array}{l}{\left(AC\right)}^2={\left(AB\right)}^2+{\left(BC\right)}^2\\ {\left(13\right)}^2={\left(AB\right)}^2+{\left(5\right)}^2\\ {\left(AB\right)}^2=169-25\\ {\left(AB\right)}^2=144\\ AB=\sqrt{144}=12\end{array}$

The base of the pyramid is an isosceles triangle. The altitude to the base of an isosceles triangle bisects the base.

The height BE can be calculated by applying Pythagoras Theorem.

In right angled triangle BEC , we get

  $\begin{array}{l}{\left(BC\right)}^2={\left(BE\right)}^2+{\left(EC\right)}^2\\ {\left(5\right)}^2={\left(BE\right)}^2+{\left(3\right)}^2\\ {\left(BE\right)}^2=25-9\\ {\left(BE\right)}^2=16\\ BE=\sqrt{16}=4\end{array}$

Volume of pyramid $=\frac{1}{3}B\times h$

  $h=BE=4$

  $B=Areaoftriangle=\frac{1}{2}\times b\times h=\frac{1}{2}\times 6\times 4=12$

  $x=AB=12$

Volume of pyramid $=\frac{1}{3}\times 12\times 12$

Volume of pyramid $=48$