Chapter 12.5, Problem 15PSB

To determine

To prove: In a pyramid or a cone, the ratio of a cross section to the area of the base equals the square of the ratio of the figures respective distances from the vertex.

Explanation of Solution

Given information:

In a pyramid,

¢ = area of the cross section,

  $\beta =$ area of the base,

k = distance from the vertex to the cross section,

h = height of the pyramid or cone.

Formula used:

The below properties are used:

All right angles are congruent.

If two triangles are similar, then the ratio of corresponding sides are congruent.

The below similar figures theorem is used:

If two triangles are similar, then the ratio of the area of both triangles is proportional to the square of ratio of their corresponding sides. This proves that the ratio of the area of two similar triangles is proportional to the squares of the corresponding sides of both the triangles.

Proof:

  

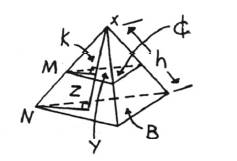
Altitudes form right angles.

  $\angle XYM$ is a right angle.

  $\angle XZN$ is a right angle.

All right angles are congruent.

  $\angle XYM\cong \angle XZN$

By reflexive property, we get

  $\angle MXY\cong \angle MXY$

Two triangles are congruent by AA similarity rule.

  $\Delta WYN\cong \Delta XZN$

If two triangles are similar, then the ratio of corresponding sides are congruent.

  $\frac{k}{h}=\frac{XM}{ZN}----Equation1$

By Similar Figures Theorem, we get

  ${\left(\frac{XM}{ZN}\right)}^2=\frac{¢}{\beta }----Equation2$

From Equation 1 and Equation 2, we get

  ${\left(\frac{k}{h}\right)}^2=\frac{¢}{\beta }$