Chapter 12.4, Problem 20PSC

a.

To determine

To calculate: The volume of ice in each cube.

Answer to Problem 20PSC

The volume of ice in each cube is $51.4c{m}^3$ .

Explanation of Solution

Given information:

An ice cube manufacturer makes ice cubes with holes in them. Each cube is 4 cm on a side and hole is 2 cm in diameter.

Formula used:

Volume of cube $=s^3$

Where s = side of cube

Volume of hole $=\pi r^{2}h$

r = radius of hole,

h = height of hole.

Calculation:

  

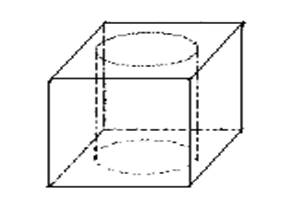
Volume of cube $=s^3$

Each cube is 4 cm.

Volume of cube $={\left(4\right)}^3$

Volume of cube $=64c{m}^3$

Volume of hole $=\pi r^{2}h$

Volume of hole $=\pi {\left(1\right)}^2\times 4$

Volume of hole $=4\times 3.14$

Volume of hole $=12.56c{m}^3$

Volume of ice = Volume of cube − Volume of hole

Volume of ice $=64-12.56$

Volume of ice $=51.4c{m}^3$

b.

To determine

To find: The volume of water left when 10 cubes will melt.

Answer to Problem 20PSC

The volume of water left is $457.8c{m}^3$ .

Explanation of Solution

Given information:

An ice cube manufacturer makes ice cubes with holes in them. Each cube is 4 cm on a side and hole is 2 cm in diameter.

Water volume decreases by $11\%$ when it changes from solid to liquid.

Formula used:

Volume of cube $=s^3$

Where s = side of cube Volume of hole $=\pi r^{2}h$

r = radius of hole,

h = height of hole.

Calculation:

  

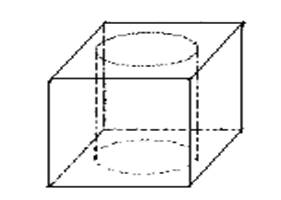
Volume of cube $=s^3$

Each cube is 4 cm.

Volume of cube $={\left(4\right)}^3$

Volume of cube $=64c{m}^3$

Volume of hole $=\pi r^{2}h$

Volume of hole $=\pi {\left(1\right)}^2\times 4$

Volume of hole $=4\times 3.14$

Volume of hole $=12.56c{m}^3$

Volume of ice = Volume of cube − Volume of hole

Volume of ice $=64-12.56$

Volume of ice $=51.4c{m}^3$

Volume of 10 cubes $\approx 10\times 51.44\approx 514.4c{m}^3$

Water volume decreases by $11\%$ when it changes from solid to liquid.

Volume of 10 melted cubes $\approx 514.4-(11\%\times 514.4)$

Volume of 10 melted cubes $\approx 0.89\times 514.4\approx 457.8c{m}^3$

c.

To determine

To calculate: The total surface area of a single cube.

Answer to Problem 20PSC

The total surface area of a single cube is $114.8c{m}^2$ .

Explanation of Solution

Given information:

An ice cube manufacturer makes ice cubes with holes in them. Each cube is 4 cm on a side and hole is 2 cm in diameter.

Formula used:

Facial area of the cube $=s^2$

where s = side of cube.

Base area of cylinder $=\pi r^2$

where r = radius of cylinder

Lateral area of cylinder $=Ch$

where $C=2\pi r$ is the circumference of cylinder

r = radius of cylinder

h = height of cylinder.

Calculation:

  

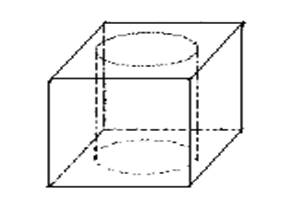
Facial area of the cube $=s^2$

Facial area of the cube $={\left(4\right)}^2$

Facial area of the cube $=16$

Base area of cylinder $=\pi r^2$

  $\begin{array}{l}d=2\\ r=\frac{d}{2}=\frac{2}{2}=1\end{array}$

Base area of cylinder $=\pi {\left(1\right)}^2$

Base area of cylinder $=\pi$

Lateral area of cylinder $=Ch$

  $C=2\pi r=2\pi \times 1=2\pi$

  $h=4$

Lateral area of cylinder $=2\pi \times 4$

Lateral area of cylinder $=8\pi$

Total Area = 6(Facial area of the cube) − 2(Base area of cylinder) + Lateral area of cylinder

Total Area $=\left(6\times 16\right)-2\pi +8\pi$

Total Area $=96-2\left(3.142\right)+8\left(3.142\right)$

Total Area $=114.8c{m}^2$

d.

To determine

To verify: The total surface area of a cube is twice the total surface area of cube without holes.

Explanation of Solution

Given information:

An ice cube manufacturer makes ice cubes with holes in them. Each cube is 4 cm on a side and hole is 2 cm in diameter.

The manufacture claims that these cube cool a drink twice as fast regular cubes of the same size.

Formula used:

Facial area of the cube $=s^2$

where s = side of cube.

Base area of cylinder $=\pi r^2$

where r = radius of cylinder

Lateral area of cylinder $=Ch$

where $C=2\pi r$ is the circumference of cylinder

r = radius of cylinder

h = height of cylinder.

Proof:

  

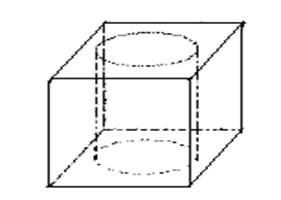
Facial area of the cube $=s^2$

Facial area of the cube $={\left(4\right)}^2$

Facial area of the cube $=16$

Base area of cylinder $=\pi r^2$

  $\begin{array}{l}d=2\\ r=\frac{d}{2}=\frac{2}{2}=1\end{array}$

Base area of cylinder $=\pi {\left(1\right)}^2$

Base area of cylinder $=\pi$

Lateral area of cylinder $=Ch$

  $C=2\pi r=2\pi \times 1=2\pi$

  $h=4$

Lateral area of cylinder $=2\pi \times 4$

Lateral area of cylinder $=8\pi$

Total Area = 6(Facial area of the cube) − 2(Base area of cylinder) + Lateral area of cylinder

Total Area $=\left(6\times 16\right)-2\pi +8\pi$

Total Area $=96-2\left(3.142\right)+8\left(3.142\right)$

Total Area $=114.8c{m}^2$

Total area of a cube without hole $=6{\left(s\right)}^2$

Total area of a cube without hole $=6{\left(4\right)}^2$

Total area of a cube without hole $=96c{m}^2$

The ratio of area is as follows.

  $\frac{Totalareaofacube}{Totalareaofacubewithouthole}=\frac{114.8}{96}=1.20$

The manufacturer claim is not true because the ratio is not two.