Chapter 12.3, Problem 14PSC

a.

To determine

To calculate: The total area of a cone frustum if slant height is 5.

Answer to Problem 14PSC

The total area of frustum is $99\pi$ .

Explanation of Solution

Given information:

Radius of top base = 3,

Radius of bottom base = 6,

Angle at base of bottom cone $={60}^{\circ }$ ,

Formula used:

Area of cone $=\frac{1}{2}\times C\times l$

C = Circumference of cone and l = slant height of cone

r = radius of circle

Area of a circle: $A=\pi r^2$

r = radius of circle

Calculation:

  

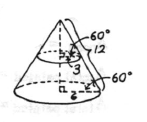
The surface forms frustum of a cone. Extend the frustum to form a cone’

There are two ${30}^{\circ }{60}^{\circ }{90}^{\circ }\Delta \text{'}s$ formed with parallel bases.

In large triangle, hypotenuse = length of cone =12

The converse of Midline theorem is used. Midline theorem states that the segment that joins the midpoints of two sides of a triangle is parallel to the third side and half as long

In small triangle, hypotenuse $=2\times 3=6$

Circumference of top cone: $C=2\pi r=2\pi \times 3=6\pi$

Lateral Area of top cone $=\frac{1}{2}\times C\times h$

Lateral Area of top cone $=\frac{1}{2}\times 6\pi \times 6$

Lateral Area of top cone $=18\pi$

Circumference of bottom cone: $C=2\pi r=2\pi \times 6=12\pi$

Lateral Area of bottom cone $=\frac{1}{2}\times C\times h$

Lateral Area of bottom cone $=\frac{1}{2}\times 12\pi \times 12$

Lateral Area of bottom cone $=72\pi$

Difference in Lateral Area $=72\pi -18\pi =54\pi$

Area of top base circle $=\pi {\left(6\right)}^2=36\pi$

Area of bottom base circle $=\pi {\left(3\right)}^2=9\pi$

Total Area = Area of bottom base circle + Area of top base circle + Difference in Lateral Area

Total Area $=9\pi +36\pi +54\pi$

Total Area $=99\pi$

b.

To determine

To find: The total area of a cylindrical shell with height as 5.

Answer to Problem 14PSC

The total area of cylindrical shell is $60\pi$ .

Explanation of Solution

Given information:

Radius of smaller circle = 2,

Height of cylinder = 5.

Formula used:

Area of cylinder $=C\times h$

C = Circumference of cylinder and h = height of cylinder

Area of a circle: $A=\pi r^2$

r = radius of circle

Calculation:

  

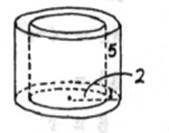
The surface forms cylindrical shell.

Radius of smaller circle = 2

Radius of larger circle $=2+1=3$

Height of cylinder = 5.

Circumference of larger cylinder: $C=2\pi r=2\pi \times 3=6\pi$

Lateral Area of larger cylinder $C\times h$

Lateral Area of larger cylinder $=6\pi \times 5$

Lateral Area of larger cylinder $=30\pi$

Circumference of smaller cylinder: $C=2\pi r=2\pi \times 2=4\pi$

Lateral Area of smaller cylinder $=C\times h$

Lateral Area of smaller cylinder $=4\pi \times 5$

Lateral Area of smaller cylinder $=20\pi$

Area of larger circle $=\pi {\left(3\right)}^2=9\pi$

Area of smaller circle $=\pi {\left(2\right)}^2=4\pi$

Total Area = Area of larger cylinder + Area of smaller cylinder + 2(Area of larger circle - Area of smaller circle)

Total Area $=30\pi +20\pi +2\left(9\pi -4\pi \right)$

Total Area $=50\pi +10\pi$

Total Area $=60\pi$

c.

To determine

To calculate: The total area of a solid.

Answer to Problem 14PSC

The total area of solid is $424\pi$ .

Explanation of Solution

Given information:

Radius = 8,

Height of cylinder = 10,

Slant height of cone = 17.

Formula used:

The below theorem is used:

Pythagoras theorem states that “In a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”.

  

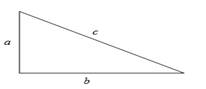
In right angle triangle,

  $a^2+b^2\text{= }{c}^2$

Area of cylinder $=C\times h$

C = Circumference of cylinder and h = height of cylinder

Area of cone $=\frac{1}{2}\times C\times l$

C = Circumference of cone and l = slant height of cone

Area of hemisphere $=\frac{1}{2}\times 4\pi r^2$

r = radius of hemisphere

Calculation:

  

  $r=8$

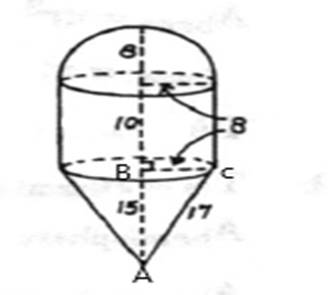
Side AB can be calculated by applying Pythagoras Theorem.

In right angled triangle ABC , we get

  $\begin{array}{l}{\left(AC\right)}^2={\left(AB\right)}^2+{\left(BC\right)}^2\\ {\left(17\right)}^2={\left(AB\right)}^2+{\left(8\right)}^2\\ 289={\left(AB\right)}^2+64\\ {\left(AB\right)}^2=289-64\\ {\left(AB\right)}^2=225\\ AB=\sqrt{225}\\ AB=15\end{array}$

Height of cone $AB=15$

Slant height of cone = 17.

Height of cylinder $=10$ .

Area of cylinder $=C\times h$

  $C=2\pi \times 8=16\pi$

  $h=10$

Area of cylinder $=16\pi \times 10$

Area of cylinder $=160\pi$

Area of cone $=\frac{1}{2}\times C\times l$

  $C=2\pi \times 8=16\pi$

  $l=17$

Area of cone $=\frac{1}{2}\times C\times l$

Area of cone $=\frac{1}{2}\times 16\pi \times 17$

Area of cone $=136\pi$

Area of hemisphere $=\frac{1}{2}\times 4\pi r^2$

Area of hemisphere $=2\pi {\left(8\right)}^2$

Area of hemisphere $=128\pi$

Total Area = Area of cylinder + Area of cone + Area of hemisphere

Total Area $=160\pi +136\pi +128\pi$

Total Area $=424\pi$