Chapter 12.2, Problem 4PSA

a.

To determine

To find: The face ABCD belongs to solid.

Answer to Problem 4PSA

No, face ABCD is not a face of solid.

Explanation of Solution

Given information:

A solid comprising of a prism and regular pyramid.

Side AE = EF=FB=AB=CB=CG=FG=BF=HG=CD=DH =AD=EH= 10

Side PA=PB=PC=PD= 13

  

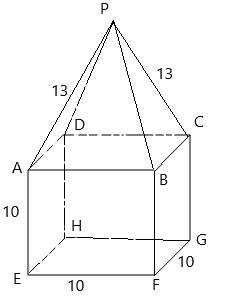
A solid comprises of a prism and regular pyramid. A face is said to be on solid if it on the surface of solid. It is evident from figure that face ABCD lies between a prism and pyramid. All other faces like PBC, PAB, PDA, PDC, ABFE, BFGC, DCGH, ADHE and FGHE lie on solid as they are on the surface of solid.

Thus, face ABCD is not a face of solid.

b.

To determine

To calculate: The number of faces of solid.

Answer to Problem 4PSA

The number of faces of solid is $9$ .

Explanation of Solution

Given information:

A solid comprising of a prism and regular pyramid.

Side AE = EF=FB=AB=CB=CG=FG=BF=HG=CD=DH =AD=EH= 10

Side PA=PB=PC=PD= 13

  

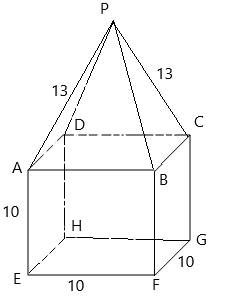
A solid comprises of a prism and regular pyramid. A face is said to be on solid if it on the surface of solid. It is evident from figure that face ABCD lies between a prism and pyramid. All other faces like PBC, PAB, PDA, PDC, ABFE, BFGC, DCGH, ADHE and FGHE lie on solid as they are on the surface of solid. Face ABCD is not a face of solid.

There are nine faces of solid.

c.

To determine

To calculate: The total area of solid.

Answer to Problem 4PSA

The total area of solid is $740$ .

Explanation of Solution

Given information:

A solid comprising of a prism and regular pyramid.

Side AE = EF=FB=AB=CB=CG=FG=BF=HG=CD=DH =AD=EH= 10

Side PA=PB=PC=PD= 13

Formula used:

The below theorem is used:

Pythagoras theorem states that “In a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”.

  

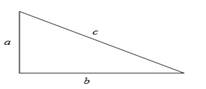
In right angle triangle,

  $a^2+b^2\text{= }{c}^2$

Area of triangle: $A=\frac{1}{2}\times b\times h$

b = base of triangle

h = height of triangle

Area of square: $A=s^2$

s = side of square

Calculation:

  

Area of base = Area of square $={\left(10\right)}^2=100$

Lateral area of bottom= 4 $\times$ Area of square

Lateral area of bottom= 4 $\times$ 100

Lateral area of bottom= 400

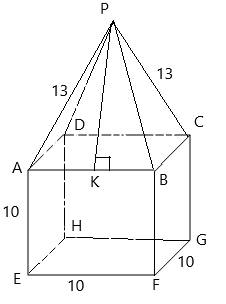
Draw altitude perpendicular to base.

The altitude AK can be calculated by applying Pythagoras Theorem.

In right angle triangle AKB , we get

  $\begin{array}{l}{\left(AK\right)}^2+{\left(KB\right)}^2={\left(AB\right)}^2\\ {\left(AK\right)}^2+{\left(5\right)}^2={\left(13\right)}^2\\ {\left(AK\right)}^2+25=169\\ {\left(AK\right)}^2=169-25\\ {\left(AK\right)}^2=144\\ AK=\sqrt{144}=12\end{array}$

The altitude AK drawn perpendicular divides the triangle face into two right triangles of $12-5-13$ family.

Lateral area of regular pyramid = 4 $\times$ Area of triangle

Lateral area of regular pyramid $=4\times \left(\frac{1}{2}\times b\times h\right)$

Lateral area of regular pyramid $=4\times \left(\frac{1}{2}\times 10\times 12\right)$

Lateral area of regular pyramid $=240$

Total Area = Area of base + Lateral area of bottom prism + Lateral area of regular pyramid

Total Area $=100+400+240$

Total Area $=740$