Chapter 12.5, Problem 14PSB

a.

To determine

To calculate: The value of x .

Answer to Problem 14PSB

The value of x is $15$ .

Explanation of Solution

Given information:

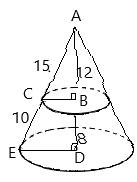
Height of small cone = 12,

Slant height of small cone = x ,

Height of large cone $=12+8=20,$

Slant height of large cone $=x+10.$

Formula used:

The below property is used:

Corresponding sides of similar triangles are congruent.

Calculation:

  

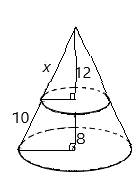
The smaller triangle is similar to the whole triangle by AA similarity rule, so

Corresponding sides of similar triangles are congruent.

  $\begin{array}{l}\frac{x}{x+10}=\frac{12}{12+8}\\ \frac{x}{x+10}=\frac{12}{20}\\ 20x=12x+120\\ 8x=120\\ x=\frac{120}{8}=15\end{array}$

b.

To determine

To find: The radii of the circles.

Answer to Problem 14PSB

The radii are 9 and 15.

Explanation of Solution

Given information:

Height of small cone = 12,

Slant height of small cone = x ,

Height of large cone $=12+8=20,$

Slant height of large cone $=x+10.$

Formula used:

The below property is used:

Corresponding sides of similar triangles are congruent.

The below theorem is used:

Pythagoras theorem states that “In a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”.

  

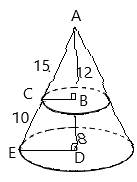
In right angle triangle,

  $a^2+b^2\text{= }{c}^2$

Calculation:

  

The smaller triangle is similar to the whole triangle by AA similarity rule, so

Corresponding sides of similar triangles are congruent.

  $\begin{array}{l}\frac{x}{x+10}=\frac{12}{12+8}\\ \frac{x}{x+10}=\frac{12}{20}\\ 20x=12x+120\\ 8x=120\\ x=\frac{120}{8}=15\end{array}$

Radius of small circle:

Side BC can be calculated by applying Pythagoras Theorem.

In right angled triangle ABC , we get

  $\begin{array}{l}{\left(AC\right)}^2={\left(AB\right)}^2+{\left(BC\right)}^2\\ {\left(15\right)}^2={\left(12\right)}^2+{\left(BC\right)}^2\\ 225=144+{\left(BC\right)}^2\\ {\left(BC\right)}^2=225-144\\ BC=\sqrt{81}\\ BC=9\\ r=BC=9\end{array}$

Radius of large circle:

Side ED can be calculated by applying Pythagoras Theorem.

In right angled triangle ADE , we get

  $\begin{array}{l}{\left(AE\right)}^2={\left(AD\right)}^2+{\left(DE\right)}^2\\ {\left(25\right)}^2={\left(20\right)}^2+{\left(DE\right)}^2\\ 625=400+{\left(DE\right)}^2\\ {\left(DE\right)}^2=625-400\\ DE=\sqrt{225}\\ DE=15\\ r=DE=15\end{array}$

c.

To determine

To calculate: The volume of smaller cone.

Answer to Problem 14PSB

The volume of smaller cone is $1018$ .

Explanation of Solution

Given information:

Height of small cone = 12,

Slant height of small cone = x ,

Height of large cone $=12+8=20,$

Slant height of large cone $=x+10.$

Formula used:

The below property is used:

Corresponding sides of similar triangles are congruent.

The below theorem is used:

Pythagoras theorem states that “In a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”.

  

In right angle triangle,

  $a^2+b^2\text{= }{c}^2$

Volume of cone $=\frac{1}{3}\times B\times h$

B = Base area of cone and h = height of cone

Area of a circle: $A=\pi r^2$

r = radius of circle

Calculation:

  

The smaller triangle is similar to the whole triangle by AA similarity rule, so

Corresponding sides of similar triangles are congruent.

  $\begin{array}{l}\frac{x}{x+10}=\frac{12}{12+8}\\ \frac{x}{x+10}=\frac{12}{20}\\ 20x=12x+120\\ 8x=120\\ x=\frac{120}{8}=15\end{array}$

Radius of small circle:

Side BC can be calculated by applying Pythagoras Theorem.

In right angled triangle ABC , we get

  $\begin{array}{l}{\left(AC\right)}^2={\left(AB\right)}^2+{\left(BC\right)}^2\\ {\left(15\right)}^2={\left(12\right)}^2+{\left(BC\right)}^2\\ 225=144+{\left(BC\right)}^2\\ {\left(BC\right)}^2=225-144\\ BC=\sqrt{81}\\ BC=9\\ r=BC=9\end{array}$

Volume of cone $=\frac{1}{3}\times B\times h$

  $B=\pi r^2=\pi {\left(9\right)}^2=81\pi$

  $h=12$

Volume of smaller cone $=\frac{1}{3}\times 81\pi \times 12$

Volume of smaller cone $=324\pi$

Volume of smaller cone $\approx 1018$

d.

To determine

To calculate: The volume of larger cone.

Answer to Problem 14PSB

The volume of larger cone is $4712$ .

Explanation of Solution

Given information:

Height of small cone = 12,

Slant height of small cone = x ,

Height of large cone $=12+8=20,$

Slant height of large cone $=x+10.$

Formula used:

The below property is used:

Corresponding sides of similar triangles are congruent.

The below theorem is used:

Pythagoras theorem states that “In a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”.

  

In right angle triangle,

  $a^2+b^2\text{= }{c}^2$

Volume of cone $=\frac{1}{3}\times B\times h$

B = Base area of cone and h = height of cone

Area of a circle: $A=\pi r^2$

r = radius of circle

Calculation:

  

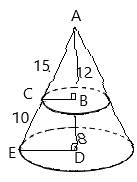
The smaller triangle is similar to the whole triangle by AA similarity rule, so

Corresponding sides of similar triangles are congruent.

  $\begin{array}{l}\frac{x}{x+10}=\frac{12}{12+8}\\ \frac{x}{x+10}=\frac{12}{20}\\ 20x=12x+120\\ 8x=120\\ x=\frac{120}{8}=15\end{array}$

Radius of large circle:

Side ED can be calculated by applying Pythagoras Theorem.

In right angled triangle ADE , we get

  $\begin{array}{l}{\left(AE\right)}^2={\left(AD\right)}^2+{\left(DE\right)}^2\\ {\left(25\right)}^2={\left(20\right)}^2+{\left(DE\right)}^2\\ 625=400+{\left(DE\right)}^2\\ {\left(DE\right)}^2=625-400\\ DE=\sqrt{225}\\ DE=15\\ r=DE=15\end{array}$

Volume of cone $=\frac{1}{3}\times B\times h$

  $B=\pi r^2=\pi {\left(15\right)}^2=225\pi$

  $h=20$

Volume of larger cone $=\frac{1}{3}\times 225\pi \times 20$

Volume of larger cone $=1500\pi$

Volume of larger cone $\approx 4712$

e.

To determine

To calculate: The volume of the frustum.

Answer to Problem 14PSB

The volume of the frustum is $3695$ .

Explanation of Solution

Given information:

Height of small cone = 12,

Slant height of small cone = x ,

Height of large cone $=12+8=20,$

Slant height of large cone $=x+10.$

Formula used:

The below property is used:

Corresponding sides of similar triangles are congruent.

The below theorem is used:

Pythagoras theorem states that “In a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”.

  

In right angle triangle,

  $a^2+b^2\text{= }{c}^2$

Volume of cone $=\frac{1}{3}\times B\times h$

B = Base area of cone and h = height of cone

Area of a circle: $A=\pi r^2$

r = radius of circle

Calculation:

  

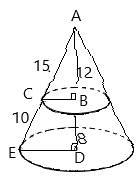
The smaller triangle is similar to the whole triangle by AA similarity rule, so

Corresponding sides of similar triangles are congruent.

  $\begin{array}{l}\frac{x}{x+10}=\frac{12}{12+8}\\ \frac{x}{x+10}=\frac{12}{20}\\ 20x=12x+120\\ 8x=120\\ x=\frac{120}{8}=15\end{array}$

Radius of small circle:

Side BC can be calculated by applying Pythagoras Theorem.

In right angled triangle ABC , we get

  $\begin{array}{l}{\left(AC\right)}^2={\left(AB\right)}^2+{\left(BC\right)}^2\\ {\left(15\right)}^2={\left(12\right)}^2+{\left(BC\right)}^2\\ 225=144+{\left(BC\right)}^2\\ {\left(BC\right)}^2=225-144\\ BC=\sqrt{81}\\ BC=9\\ r=BC=9\end{array}$

Volume of cone $=\frac{1}{3}\times B\times h$

  $B=\pi r^2=\pi {\left(9\right)}^2=81\pi$

  $h=12$

Volume of smaller cone $=\frac{1}{3}\times 81\pi \times 12$

Volume of smaller cone $=324\pi$

Volume of smaller cone $\approx 1018$

Radius of large circle:

Side ED can be calculated by applying Pythagoras Theorem.

In right angled triangle ADE , we get

  $\begin{array}{l}{\left(AE\right)}^2={\left(AD\right)}^2+{\left(DE\right)}^2\\ {\left(25\right)}^2={\left(20\right)}^2+{\left(DE\right)}^2\\ 625=400+{\left(DE\right)}^2\\ {\left(DE\right)}^2=625-400\\ DE=\sqrt{225}\\ DE=15\\ r=DE=15\end{array}$

Volume of cone $=\frac{1}{3}\times B\times h$

  $B=\pi r^2=\pi {\left(15\right)}^2=225\pi$

  $h=20$

Volume of larger cone $=\frac{1}{3}\times 225\pi \times 20$

Volume of larger cone $=1500\pi$

Volume of larger cone $\approx 4712$

Volume of frustum = Volume of larger cone − Volume of smaller cone

Volume of frustum $=1500\pi -324\pi$

Volume of frustum $=1176\pi$

Volume of frustum $\approx 3695$