Chapter 11.8, Problem 27AYU

Maximizing Profil on Ice Skates A factory manufactures two kinds of ice skates: racing skates and figure skates. The racing skates require 6 work-hours in the fabrication department, whereas the figure skates require 4 work-hours there. The racing skates require 1 work-hour in the finishing department, whereas the figure skates require 2 work-hours there. The fabricating department has available at most 120 work-hours per day, and the finishing department has no more than 40 work-hours per day available. If the profit on each racing skate is $\$10$ and the profit on each figure skate is $\$12$, how many of each should be manufactured each day to maximize profit? (Assume that all skates made are sold.)

To determine

To solve: The given linear programming problem.

Answer to Problem 27AYU

Solution:

The factory has to manufacture 10 racing skates and 15 figure skates.

Explanation of Solution

Given:

• A factory manufactures racing skates and figure skates.
• Racing skates require 6 work-hours in the fabrication department and 1 work-hour in the finishing department.
• Figure skates require 4 work-hours in the fabrication department and 2 work-hour in the finishing department.
• Fabricating department has available at most 120 work-hours per day and finishing department has no more than 40 work-hours per day available.
• Profit on each racing skate is $\$10$ and profit on each figure skate is $\$12$.

Calculation:

Begin by assigning symbols for the two variables.

$x$ be the number racing skates manufactured.

$y$ be the number figure skates manufactured.

If $P$ is the total profit then,

$P=10x+12y$

The goal is to maximize $P$ subject to certain constraints on $x\text{and}y$. Because $x\text{and}y$ represents number of skates to be produced, the only meaningful values of $x\text{and}y$ are non-negative.

Therefore, $x\ge 0,y\ge 0$.

From the given data we get,

$6x+4y\le 120$   $\Rightarrow 3x+2y\le 60$

$x+2y\le 40$

Therefore, the linear programming problem may be stated as,

Maximize, $P=10x+12y$.

Subject to,

$x\ge 0$

$y\ge 0$

$3x+2y\le 60$

$x+2y\le 40$

The graph of the constraints is illustrated in the figure below.

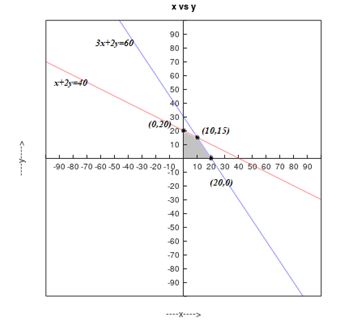
The corner points are as follows:

Corner points are	Value of objective function
(20,0)	200
(10,15)	280
(0,20)	240

Therefore, the factory has to manufacture 10 racing skates and 15 figure skates.