
Concept explainers
Waves in the Earth and the Ocean
In December 2004, a large earthquake off the coast of Indonesia produced a devastating water wave, called a tsunami, that caused tremendous destruction thousands of miles away from the earthquake's epicenter. The tsunami was a dramatic illustration of the energy carried by waves.
It was also a call to action. Many of the communities hardest hit by the tsunami were struck hours after the waves were generated, long after seismic waves from the earthquake that passed through the earth had been detected al distant recording stations, long after the possibility of a tsunami was first discussed. With better detection and more accurate models of how a tsunami is formed and how a tsunami propagates, the affected communities could have received advance warning. The study of physics may seem an abstract undertaking with few practical applications, but on this day a better scientific understanding of these waves could have averted tragedy.
Let’s use our knowledge of waves to explore the properties of a tsunami. In Chapter 15, we saw that a vigorous shake of one end of a rope causes a pulse to travel
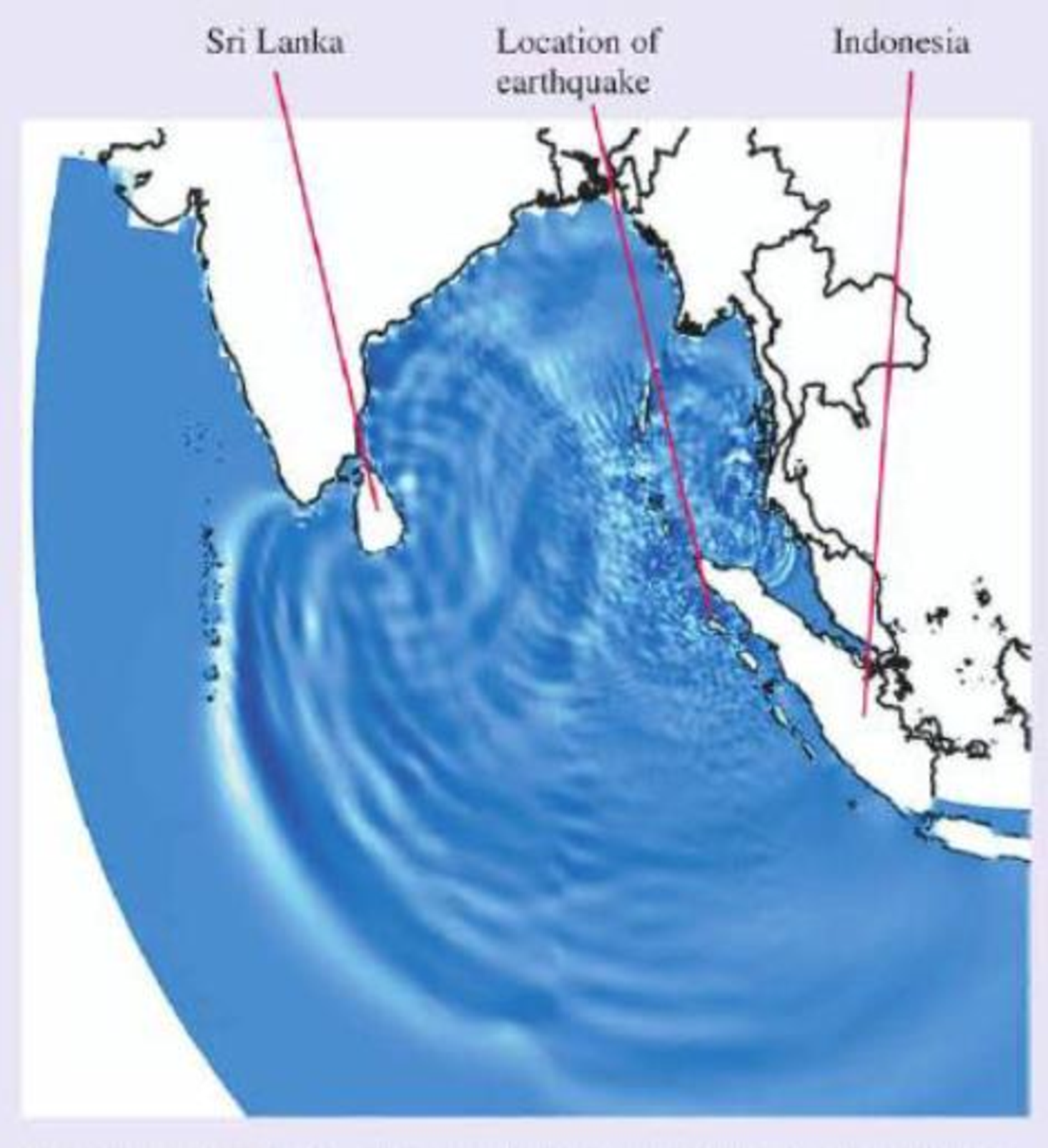
One frame from a computer simulation of the Indian Ocean tsunami three hours after the earthquake that produced it. The disturbance propagating outward from the earthquake is clearly seen, as are wave reflections from the island of Sri Lanka.
along it, carrying energy as it goes. The earthquake that produced the Indian Ocean tsunami of 2004 caused a sudden upward displacement of the seafloor that produced a corresponding rise in the surface of the ocean. This was the disturbance that produced the tsunami, very much like a quick shake on the end of a rope. The resulting wave propagated through the ocean, as we see in the figure.
This simulation of the tsunami looks much like the ripples that spread when you drop a pebble into a pond. But there is a big difference—the scale. The fact that you can see the individual waves on this diagram that spans 5000 km is quite revealing. To show up so clearly, the individual wave pulses must be very wide—up to hundreds of kilometers from front to back.
A tsunami is actually a “shallow water wave,” even in the deep ocean, because the depth of the ocean is much less than the width of the wave. Consequently, a tsunami travels differently than normal ocean waves. In Chapter 15 we learned that wave speeds arc fixed by the properties of the medium. That is true for normal ocean waves, but the great width of the wave causes a tsunami to “feel the bottom.” Its wave speed is determined by the depth of the ocean: The greater the depth, the greater the speed. In the deep ocean, a tsunami travels at hundreds of kilometers per hour, much faster than a typical ocean wave. Near shore, as the ocean depth decreases, so docs the speed of the wave.
The height of the tsunami in the open ocean was about half a meter. Why should such a small wave—one that ships didn't even notice as it passed—be so fearsome? Again, it's the width of the wave that matters. Because a tsunami is the wave motion of a considerable mass of water, great energy is involved. As the front of a tsunami wave nears shore, its speed decreases, and the back of the wave moves faster than the front. Consequently, the width decreases. The water begins to pile up, and the wave dramatically increases in height.
The Indian Ocean tsunami had a height of up to 15 m when it reached shore, with a width of up to several kilometers. This tremendous mass of water was still moving at high speed, giving it a great deal of energy. A tsunami reaching the shore isn’t like a typical wave that breaks and crashes. It is a kilometers-wide wall of water that moves onto the shore and just keeps on coming. In many places, the water reached 2 km inland.
The impact of the Indian Ocean tsunami was devastating, but it was the first tsunami for which scientists were able to use satellites and ocean sensors to make planet-wide measurements. An analysis of the data has helped us better understand the physics of these ocean waves. We won’t be able to stop future tsunamis, but with a better knowledge of how they are formed and how they travel, we will be better able to warn people to get out of their way.
The following questions are related to the passage “Waves in the Earth and the Ocean” on the previous page.
If a train of pulses moves into shallower water as it approaches a shore,
A. The wavelength increases.
B. The wavelength stays the same.
C. The wavelength decreases.
Want to see the full answer?
Check out a sample textbook solution
Chapter P Solutions
College Physics: A Strategic Approach (3rd Edition)
Additional Science Textbook Solutions
Biology: Life on Earth (11th Edition)
Microbiology with Diseases by Body System (5th Edition)
Campbell Biology in Focus (2nd Edition)
Genetic Analysis: An Integrated Approach (3rd Edition)
Microbiology: An Introduction
Anatomy & Physiology (6th Edition)
- Physics different from a sea breeze from a land breezearrow_forwardFile Preview Design a capacitor for a special purpose. After graduating from medical school you and a friend take a three hour cruise to celebrate and end up stranded on an island. While looking for food, a spider falls on your friend giving them a heart attack. Recalling your physics, you realize you can build a make-shift defibrillator by constructing a capacitor from materials on the boat and charging it using the boat's battery. You know that the capacitor must hold 100 J of energy and be at 1000 V (fortunately this is an electric boat which has batteries that are 1000 V) to work. You decide to construct the capacitor by tightly sandwiching a single layer of Saran wrap between sheets of aluminum foil. You read the Saran wrap box and fortunately they tell you that it has a thickness 0.01 mm and dielectric constant of 2.3. The Saran wrap and foil are 40 cm wide and very long. How long is the final capacitor you build that saves your friend?arrow_forwardHow do I plot the force F in Matlba (of gravity pulling on the masses) versus spring displacement, and fit the data with a linear function to find the value for the spring constant. To get a linear fit, use polynomial order 1. Report the value of 'k' from the fit. What code is used?arrow_forward
- Ok im confused on this portion of the questions being asked. the first snip is the solution you gave which is correct. BUt now it is asking for this and im confused. The magnitude of the force F_11 is __________LB. The direction of the force F_11 is __________LB.arrow_forwardNo chatgpt pls will upvotearrow_forwardSolve and answer the problem correctly please. Thank you!!arrow_forward
- Solve and answer the problem correctly please. Thank you!!arrow_forwardSolve and answer the problem correctly and be sure to check your work. Thank you!!arrow_forwardThe spring in the figure has a spring constant of 1300 N/m. It is compressed 17.0 cm, then launches a 200 g block. The horizontal surface is frictionless, but the block’s coefficient of kinetic friction on the incline is 0.200. What distance d does the block sail through the air?arrow_forward
- Solve and answer the problem correctly and be sure to check your work. Thank you!!arrow_forwardSolve and answer the problem correctly and be sure to check your work. Thank you!!arrow_forwardA 10-m-long glider with a mass of 680 kg (including the passengers) is gliding horizontally through the air at 28 m/s when a 60 kg skydiver drops out by releasing his grip on the glider. What is the glider's speed just after the skydiver lets go?arrow_forward
 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning





