
Concept explainers
Size and Life
Physicists look for simple models and general principles that underlie and explain diverse physical phenomena. In the first 13 chapters of this textbook, you’ve seen that just a handful of general principles and laws can be used to solve a wide range of problems. Can this approach have any relevance to a subject like biology? It may seem surprising, but there are general 'laws of biology“’ that apply, with quantitative accuracy, to organisms as diverse as elephants and mice.
Let’s look at an example. An elephant uses more metabolic power than a mouse. This is not surprising, as an elephant is much bigger. But recasting the data shows an interesting trend. When we looked at the energy required to raise the temperature of different substances, we considered specific heat. The “specific” meant that we considered the heat required for 1 kilogram. For animals, rather than metabolic rate, we can look at the specific metabolic rate, the metabolic power used per kilogram of tissue. If we factor out the mass difference between a mouse and an elephant, are their specific metabolic powers the same?
In fact, the specific metabolic rate varies quite a bit among mammals, as the graph of specific metabolic rate versus mass shows. But there is an interesting trend: All of the data points lie on a single smooth curve. In other words, there really is a biological law we can use to predict a mammal’s metabolic rate knowing only its mass M. In particular, the specific metabolic rate is proportional to M –0.25. Because a 4000 kg elephant is 160,000 times more massive than a 25 g mouse, the mouse’s specific metabolic power is (160,000)0.25 = 20 times that of the elephant. A law that shows how a property scales with the size of a system is called a scaling law.
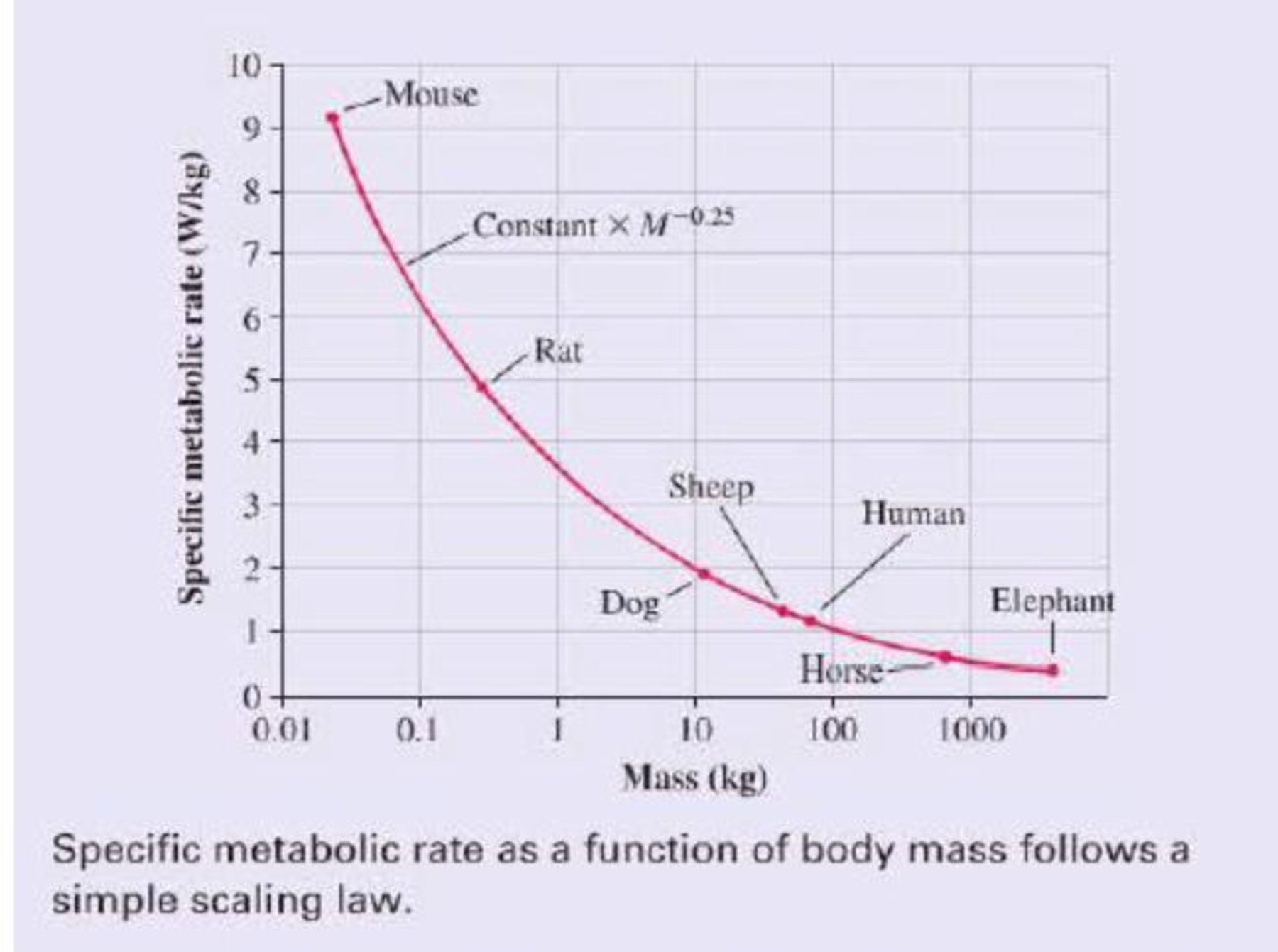
A similar scaling law holds for birds, reptiles, and even bacteria. Why should a single simple relationship hold true for organisms that range in size from a single cell to a 100 ton blue whale? Interestingly, no one knows for sure. It is a matter of current research to find out just what this and other scaling laws tell us about the nature of life.
Perhaps the metabolic-power scaling law is a result of
If heat dissipation were the only factor limiting metabolism, we can show that the specific metabolic rate should scale as M–0.33quite different from the M–0.25 scaling observed. Clearly, another factor is at work. Exactly what underlies the M–0.25 scaling is still a matter of debate, but some recent analysis suggests the scaling is due to limitations not of heat transfer but of fluid flow. Cells in mice, elephants, and all mammals receive nutrients and oxygen for metabolism from the bloodstream. Because the minimum size of a capillary is about the same for all mammals, the structure of the circulatory system must vary from animal to animal. The human aorta has a diameter of about 1 inch; in a mouse, the diameter is approximately l/20th of this. Thus a mouse has fewer levels of branching to smaller and smaller blood vessels as we move from the aorta to the capillaries. The smaller blood vessels in mice mean that viscosity is more of a factor throughout the circulatory system. The circulatory system of a mouse is quite different from that of ail elephant.
A model of specific metabolic rate based on blood-flow limitations predicts a M–0.25 law, exactly as observed. The model also makes other testable predictions. For example, the model predicts that the smallest possible mammal should have a body mass of about 1 gram—exactly the size of the smallest shrew. Even smaller animals have different types of circulatory' systems; in the smallest animals, nutrient transport is by diffusion alone. But the model can be extended to predict that the specific metabolic rate for these animals will follow a scaling law similar to that for mammals, exactly as observed. It is too soon to know if this model will ultimately prove to be correct, but it’s indisputable that there are large-scale regularities in biology that follow mathematical relationships based on the laws of physics.
The following questions are related to the passage "Size and Life" on the previous page.
Given the data of the graph, approximately how much energy, in Calories, would a 200 g rat use during the course of a day?
- A. 10
- B. 20
- C. 100
- D. 200
Want to see the full answer?
Check out a sample textbook solution
Chapter P Solutions
College Physics: A Strategic Approach (3rd Edition)
Additional Science Textbook Solutions
Cosmic Perspective Fundamentals
Campbell Biology in Focus (2nd Edition)
Campbell Biology: Concepts & Connections (9th Edition)
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Campbell Essential Biology with Physiology (5th Edition)
Chemistry: A Molecular Approach (4th Edition)
- PART III - RESISTORS IN PARALLEL Consider (but do not yet build) the circuit shown in the circuit diagram to the left, which we will call Circuit 3. Make sure you are using Bert bulbs. You may want to wire two batteries in series rather than use a single battery. 7. Predict: a) How will the brightness of bulb B3A compare to the brightness to bulb B3B? c) X E B3A b) How will the brightness of bulb BзA compare to the brightness of bulb B₁ from Circuit 1? How will the currents at points X, Y, and Z be related? www d) How will the current at point X in this circuit compare to the current at point X from Circuit 1? Y Z B3B wwwarrow_forwardPART II - RESISTORS IN SERIES Consider (but do not yet build) the circuit shown in the circuit diagram to the left, which we will call Circuit 2. Make sure you are using Bert bulbs. You may want to wire two batteries in series rather than use a single battery. 4. Predict: a) How will the brightness of bulb B₂ compare to the brighness to bulb B2B? X B2A E Y B2B Ꮓ b) How will the brightness of bulb B2A compare to the brightness of bulb B₁ from Circuit 1? c) How will the currents at points X, Y, and Z be related? d) How will the current at point X in this circuit compare to the current at point X from Circuit 1?arrow_forwardNo chatgpt pls will upvote Already got wrong chatgpt answerarrow_forward
- What is the practical benefit (in terms of time savings and efficiency) of defining the potential energy? Be clear about what is required in terms of calculation if we do not use the concept of potential energy.arrow_forwardWhat is the critical angle fir the light travelling from the crown glass(n=1.52) into the air(n=1.00)?arrow_forwardNo chatgpt pls will upvotearrow_forward
- You are working with a team that is designing a new roller coaster-type amusement park ride for a major theme park. You are present for the testing of the ride, in which an empty 150 kg car is sent along the entire ride. Near the end of the ride, the car is at near rest at the top of a 100 m tall track. It then enters a final section, rolling down an undulating hill to ground level. The total length of track for this final section from the top to the ground is 250 m. For the first 230 m, a constant friction force of 370 N acts from computer-controlled brakes. For the last 20 m, which is horizontal at ground level, the computer increases the friction force to a value required for the speed to be reduced to zero just as the car arrives at the point on the track at which the passengers exit. (a) Determine the required constant friction force (in N) for the last 20 m for the empty test car. Write AK + AU + AE int = W+Q + TMW + TMT + TET + TER for the car-track-Earth system and solve for…arrow_forward= 12 kg, and m3 Three objects with masses m₁ = 3.8 kg, m₂ find the speed of m3 after it moves down 4.0 m. m/s 19 kg, respectively, are attached by strings over frictionless pulleys as indicated in the figure below. The horizontal surface exerts a force of friction of 30 N on m2. If the system is released from rest, use energy concepts to m m2 m3 iarrow_forwardThree objects with masses m₁ = 3.8 kg, m₂ = 12 kg, and m 19 kg, respectively, are attached by strings over frictionless pulleys as indicated in the figure below. The horizontal surface exerts a force of friction of 30 N on m2. If the system is released from rest, use energy concepts to find the speed of m¸ after it moves down 4.0 m. m/s m m2 mgarrow_forward
- In order for Jane to return to base camp, she needs to swing across a river of width D that is filled with alligators. She must swing into a wind exerting constant horizontal force F, F = 110 N, L = 40.0 m, 0 = 50.0°, and her mass to be 50.0 kg. Wind →F Tarzan! Jane (a) with what minimum speed (in m/s) must Jane begin her swing to just make it to the other side? (If Jane can make it across with zero initial velocity, enter 0.) m/s on a vine having length L and initially making an angle with the vertical (see below figure). Take D = 48.0 m, (b) Shortly after Jane's arrival, Tarzan and Jane decide to swing back across the river (simultaneously). With what minimum speed (in m/s) must they begin their swing? Assume that Tarzan has a mass of 80.0 kg. m/sarrow_forwardR=2.00 12V 2.00 4.00 4.002 What is the current in one of the 4.0 Q resistors? An isolated point charge q is located at point X. Two other points Y and Z are such that YZ2 XY. Y X What is (electric field at Y)/(electric field at Z)?arrow_forwardTwo objects (m₁ = 4.75 kg and m₂ 2.80 kg) are connected by a light string passing over a light, frictionless pulley as in the figure below. The 4.75-kg object is released from rest at a point h = 4.00 m above the table mg m (a) Determine the speed of each object when the two pass each other. m/s (b) Determine the speed of each object at the moment the 4.75-kg object hits the table. m/s (c) How much higher does the 2.80-kg object travel after the 4.75-kg object hits the table? marrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





