Chapter 9, Problem 89CP

An industrial load is modeled as a series combination of an inductor and a resistance as shown in Fig. 9.89. Calculate the value of a capacitor C across the series combination so that the net impedance is resistive at a frequency of 2 kHz.

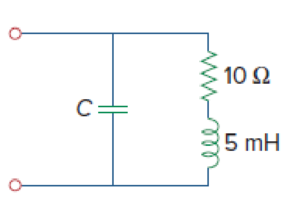
Figure 9.89

To determine

Find the value of capacitor $\left(C\right)$ when the net impedance is resistive at a frequency of $2\text{kHz}$.

Answer to Problem 89CP

When the net impedance is resistive at a frequency of $2\text{kHz}$, the value of capacitor $\left(C\right)$ is $1.235\mu \text{F}$.

Explanation of Solution

Given data:

Refer to Figure 9.89 in the textbook.

The value of frequency $\left(f\right)$ is $2\text{kHz}$.

Formula used:

Write a general expression to calculate the impedance of a resistor.

$Z_R=R$        (1)

Here,

$R$ is the value of resistance.

Write a general expression to calculate the impedance of an inductor.

$Z_L=j\omega L$        (2)

Here,

$L$ is the value of inductance, and

$\omega$ is the angular frequency.

Write a general expression to calculate the impedance of a capacitor.

$Z_C=\frac{1}{j\omega C}$        (3)

Here,

$C$ is the value of capacitance.

Write a general formula to calculate the angular frequency.

$\omega =2\pi f$        (4)

Here,

$f$ is the value of frequency.

Calculation:

Refer to the given circuit, the value of resistor $R$ is $10\Omega$ and the value of inductor $\left(L\right)$ is $5\text{mH}$.

In the given circuit, the series of combination of resistor and inductor is connected in parallel with the capacitor.

The equivalent impedance of the given circuit is written as follows using equations (1), (2) and (3).

$\begin{array}{c}{Z}_{\text{eq}}=\frac{1}{j\omega C}\parallel \left(R+j\omega L\right)\\ =\frac{\frac{1}{j\omega C}\left(R+j\omega L\right)}{R+j\omega L+\frac{1}{j\omega C}}\\ =\frac{\left(\frac{R}{j\omega C}+\frac{L}{C}\right)}{R+j\omega L-j\frac{1}{\omega C}}\\ =\frac{\left(\frac{L}{C}-j\frac{R}{\omega C}\right)}{R+j\left(\omega L-\frac{1}{\omega C}\right)}\end{array}$

Simplify the above equation as follows:

$\begin{array}{c}{Z}_{\text{eq}}=\frac{\left(\frac{L}{C}-j\frac{R}{\omega C}\right)\left(R-j\left(\omega L-\frac{1}{\omega C}\right)\right)}{R+j\left(\omega L-\frac{1}{\omega C}\right)\left(R-j\left(\omega L-\frac{1}{\omega C}\right)\right)}\\ =\frac{\left(\frac{RL}{C}-j\frac{L}{C}\left(\omega L-\frac{1}{\omega C}\right)-j\frac{R^2}{\omega C}+j^2\frac{R}{\omega C}\left(\omega L-\frac{1}{\omega C}\right)\right)}{R^2-j^2{\left(\omega L-\frac{1}{\omega C}\right)}^2}\\ =\frac{\left(\frac{RL}{C}-j\frac{L}{C}\left(\omega L-\frac{1}{\omega C}\right)-j\frac{R^2}{\omega C}+\left(-1\right)\frac{R}{\omega C}\left(\omega L-\frac{1}{\omega C}\right)\right)}{R^2-\left(-1\right){\left(\omega L-\frac{1}{\omega C}\right)}^2}\\ =\frac{\left(\frac{RL}{C}-j\frac{L}{C}\left(\omega L-\frac{1}{\omega C}\right)-j\frac{R^2}{\omega C}-\frac{R}{\omega C}\left(\omega L-\frac{1}{\omega C}\right)\right)}{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}\end{array}$

Simplify the above equation as follows:

$\begin{array}{c}{Z}_{\text{eq}}=\frac{\left(\frac{RL}{C}-j\frac{L}{C}\left(\omega L-\frac{1}{\omega C}\right)-j\frac{R^2}{\omega C}-\frac{RL}{C}+\frac{R}{{\omega }^2{C}^2}\right)}{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}\\ =\frac{\left(\frac{R}{{\omega }^2{C}^2}-j\frac{L}{C}\left(\omega L-\frac{1}{\omega C}\right)-j\frac{R^2}{\omega C}\right)}{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}\end{array}$

The equivalent impedance must be resistive when $Im\left(Z_{\text{eq}}\right)=0$

Equate the imaginary part of above equation to zero.

$\begin{array}{l}\frac{-\frac{L}{C}\left(\omega L-\frac{1}{\omega C}\right)-\frac{R^2}{\omega C}}{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}=0\\ -\frac{L}{C}\left(\omega L-\frac{1}{\omega C}\right)-\frac{R^2}{\omega C}=0\\ -L\left(\omega L-\frac{1}{\omega C}\right)-\frac{R^2}{\omega }=0\\ L\left(\omega L-\frac{1}{\omega C}\right)=-\frac{R^2}{\omega }\end{array}$

Simplify the above equation as follows:

$\begin{array}{l}\omega L-\frac{1}{\omega C}=-\frac{R^2}{\omega L}\\ \frac{1}{\omega C}=\omega L+\frac{R^2}{\omega L}\\ \frac{1}{\omega C}=\frac{{\omega }^2{L}^2+R^2}{\omega L}\\ \frac{1}{C}=\omega \left(\frac{{\omega }^2{L}^2+R^2}{\omega L}\right)\end{array}$

Simplify the above equation to find $C$.

$C=\frac{L}{R^2+{\omega }^2{L}^2}$        (5)

Substitute $2\text{kHz}$ for $f$ in equation (4) to find $\omega$.

$\begin{array}{c}\omega =2\pi \left(2\text{kHz}\right)\\ =2\pi \left(2\times {10}^3\frac{1}{\text{s}}\right)\left\{\begin{array}{l}\because 1\text{k}={10}^3\\ 1\text{Hz}=\frac{1}{\text{s}}\end{array}\right\}\\ =12566\frac{\text{rad}}{\text{s}}\end{array}$

Substitute $10\Omega$ for $R$, $12566\frac{\text{rad}}{\text{s}}$ for $\omega$, and $5\text{mH}$ for $L$ in equation (5) to find $C$.

$\begin{array}{c}C=\frac{5\text{mH}}{{\left(10\Omega \right)}^2+{\left(12566\frac{\text{rad}}{\text{s}}\right)}^2{\left(5\text{mH}\right)}^2}\\ =\frac{5\times {10}^{-3}\Omega \cdot \text{s}}{100{\Omega }^2+\left(1.58\times {10}^8\frac{{\text{rad}}^2}{{\text{s}}^2}\right){\left(5\times {10}^{-3}\Omega \cdot \text{s}\right)}^2}\left\{\begin{array}{l}\because 1\text{m}={10}^{-3}\\ 1\text{H}=1\Omega \cdot 1\text{s}\end{array}\right\}\\ =\frac{5\times {10}^{-3}\Omega \cdot \text{s}}{100{\Omega }^2+\left(1.58\times {10}^8\frac{{\text{rad}}^2}{{\text{s}}^2}\right)\left(25\times {10}^{-6}{\Omega }^2\cdot {\text{s}}^2\right)}\\ =\frac{5\times {10}^{-3}\Omega \cdot \text{s}}{100{\Omega }^2+3950{\Omega }^2}\end{array}$

Simplify the above equation as follows:

$\begin{array}{c}C=\frac{5\times {10}^{-3}\Omega \cdot \text{s}}{4050{\Omega }^2}\\ =1.235\times {10}^{-6}\frac{\text{s}}{\Omega }\\ =1.235\mu \text{F}\left\{\begin{array}{l}\because 1\mu ={10}^{-6}\\ 1\text{F}=\frac{1\text{s}}{1\Omega }\end{array}\right\}\end{array}$

Conclusion:

Thus, when the net impedance is resistive at a frequency of $2\text{kHz}$, the value of capacitor $\left(C\right)$ is $1.235\mu \text{F}$.