Chapter 8.3, Problem 48AYU

a.

To determine

How far is it from the pitching rubber to first base?

Answer to Problem 48AYU

  $\boxed{\text{42}.\text{58 feet}}$

Explanation of Solution

Given information:

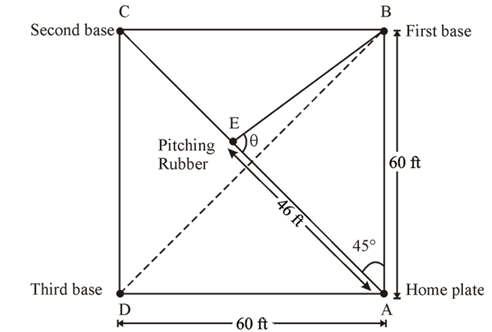
According to Little League baseball official regulations, the diamond is a square 60 feet on a side. The pitching rubber is located 46 feet from home plate on a line joining home plate and second base.

How far is it from the pitching rubber to first base?

  

Calculation:

Consider the following facts about the Little League baseball field:

The diamond is a square with length of the side 60 feet.

The distance between pitching rubber and home plate is 46 feet.

And the pitching rubber is on the line joining home plate and second base.

According to these facts we draw the following figure.

Now in the $\Delta ABE$ .

We have $AE=46ft,AB=60ft$ and $\angle BAE=45°$

By using the Law of Cosines,

  $a^2=b^2+c^2-2bc\cos A$

We get,

  $\begin{array}{l}{\left(BE\right)}^2={\left(AE\right)}^2+{\left(AB\right)}^2-2\left(AE\right)\left(AB\right)\cos \left(\angle BAE\right)\\ {\left(BE\right)}^2={\left(46\right)}^2+{\left(60\right)}^2-2\left(46\right)\left(60\right)\times \cos 45°\\ {\left(BE\right)}^2=2116+3600-2\left(46\right)\left(60\right)\times \frac{1}{\sqrt{2}}\end{array}$

  $\begin{array}{l}{\left(BE\right)}^2=1812.77\\ BE=\sqrt{1812.77}\end{array}$

  $BE=42.58$

Hence, the distance between the pitching rubber and the first base is 42.58 feet.

b.

To determine

How far is it from the pitching rubber to second base?

Answer to Problem 48AYU

  $\boxed{38.85feet}$

Explanation of Solution

Given information:

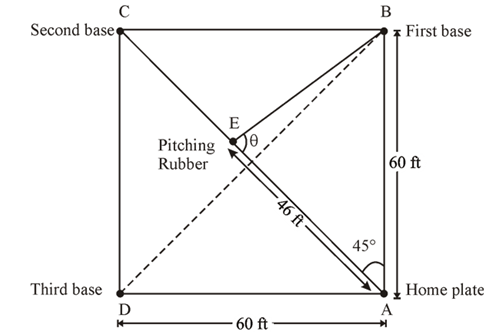
According to Little League baseball official regulations, the diamond is a square 60 feet on a side. The pitching rubber is located 46 feet from home plate on a line joining home plate and second base.

How far is it from the pitching rubber to second base?

  

Calculation:

Consider the following facts about the Little League baseball field:

The diamond is a square with length of the side 60 feet.

The distance between pitching rubber and home plate is 46 feet.

And the pitching rubber is on the line joining home plate and second base.

According to these facts we draw the following figure.

In the right angle triangle $\Delta ACD$ applying Pythagarean Theorem,

We get,

  $\begin{array}{l}{\left(AC\right)}^2={\left(AD\right)}^2+{\left(DC\right)}^2\\ {\left(AC\right)}^2={\left(60\right)}^2+{\left(60\right)}^2\\ {\left(AC\right)}^2=3600+3600\\ {\left(AC\right)}^2=7200\\ AC=\sqrt{7200}\end{array}$

  $AC=84.85$

From the figure,we have

  $CE=AC-AE$

  $CE=84.85-46$

  $CE=38.85$

Hence,the distance between the pitching rubber and the second base is $\boxed{38.85feet}$ .

c.

To determine

What angle does he need to turn to face first base?

Answer to Problem 48AYU

  $\boxed{85.18°}$

Explanation of Solution

Given information:

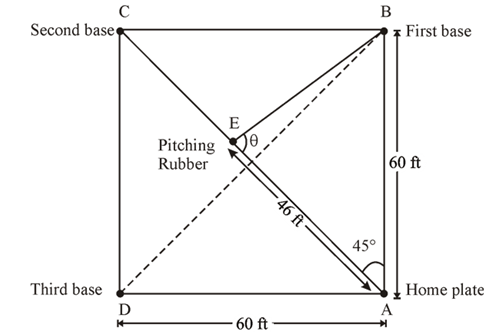
According to Little League baseball official regulations, the diamond is a square 60 feet on a side. The pitching rubber is located 46 feet from home plate on a line joining home plate and second base.

If a pitcher faces home plate, through what angle does he need to turn to face base?

  

Calculation:

Consider the following facts about the Little League baseball field:

The diamond is a square with length of the side 60 feet.

The distance between pitching rubber and home plate is 46 feet.

And the pitching rubber is on the line joining home plate and second base.

According to these facts we draw the following figure.

Using the cosine rule in triangle $\Delta ABE$ again,

We can write

  $\cos \left(\angle BEA\right)=\frac{{\left(BE\right)}^2+{\left(AE\right)}^2-{\left(AB\right)}^2}{2\left(BE\right)\left(AE\right)}$

Substiute the values of BE,AE and AB from above data,

  $\cos \left(\angle BEA\right)=\frac{{\left(42.58\right)}^2+{\left(46\right)}^2-{\left(60\right)}^2}{2\left(42.58\right)\left(46\right)}$

  $\cos \left(\angle BEA\right)=0.084$

  $\begin{array}{l}\angle BEA={\cos }^{-1}\left(0.084\right)\\ \angle BEA=85.18°\end{array}$

Hence, if a pitcher faces home plate , he need to turn at an angle of $\boxed{85.18°}$ to face first base.