Chapter 8, Problem 31RE

Finding the Grade of a Mountain Trail A straight trail with a uniform inclination leads from a hotel, elevation 5000 feet, to a lake in a valley, elevation 4100 feet. The length of the trail is 4100 feet. What is the inclination (grade) of the trail?

To determine

To find: What is the inclination (grade) of the trail?

Answer to Problem 31RE

The trail is inclined about $12.7°$ from the lake to the hotel.

Explanation of Solution

Given:

A straight trail with a uniform inclination leads from a hotel, elevation 5000 feet, to a lake in a valley, elevation 4100 feet. The length of the trail is 4100 feet.

Formula used:

$\text{sinθ }=\text{ opp}/\text{hyp}$

Calculation:

Let $A$ be the inclination of the trail.

The “rise” of the trail is $4100-5000=-900$.

$\sin A=\frac{900}{4100}$

$A={\sin }^{-1}\frac{9}{41}$

$A=12.7°$

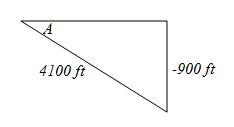
The trail is inclined about $12.7°$ from the lake to the hotel.