Chapter 8.4, Problem 39AYU

To determine

To find: The area of the shaded region.

Answer to Problem 39AYU

The area of the shaded region is $\frac{1}{2}{r}^2\left(\theta +\sin \theta \right)$ .

Explanation of Solution

Given:

The given diagram is shown in Figure

  

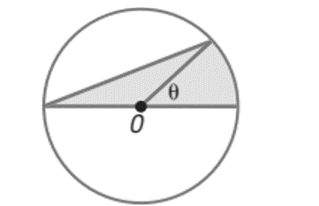
Figure 1

Calculation:

The area of the shaded region is the sum of the area of the sector and that is formed by the central angle $\theta$ and the area of the triangle.

Consider the area of the sector is,

  $A_1=\frac{1}{2}{r}^2\theta$

Consider the area of the triangle is,

  $A_2=\frac{1}{2}{r}^2\sin \left(180°-\theta \right)$

Then,

  $\begin{array}{c}K=\frac{1}{2}{r}^2\sin \left(180°-\theta \right)\\ =\frac{1}{2}{r}^2\sin \theta \end{array}$

Then, the area of the shaded region is,

  $\begin{array}{c}K=\frac{1}{2}{r}^2\sin \theta +\frac{1}{2}{r}^2\theta \\ =\frac{1}{2}{r}^2\left(\theta +\sin \theta \right)\end{array}$