Chapter 8.5, Problem 29AYU

(a)

To determine

To find: The motion of the object with the mass and the damping factor.

Answer to Problem 29AYU

The direction of the bob is negative, the mass of the bob is $m=40\text{kg}$ and the damping factor $b=0.6\text{kg}/\sec$ .

Explanation of Solution

Given:

The given covered by the bob is $d=-30e^{\frac{-0.6t}{80}}\cos \left(\sqrt{{\left(\frac{2\pi }{7}\right)}^2-\frac{0.36}{6400}t}\right)$ .

Calculation:

Consider the given equation for distance is,

  $d=-30e^{\frac{-0.6t}{80}}\cos \left(\sqrt{{\left(\frac{2\pi }{7}\right)}^2-\frac{0.36}{6400}t}\right)$

The bob is released from left to right it represents a negative direction and the motion described by the bob is damped.

Consider the general expression for the damped motion is,

  $d=-20e^{\frac{-bt}{2m}}\cos \left(\sqrt{{\omega }^2-\frac{b^2}{4m^2}t}\right)$

From the given equation and from the above equation the amplitude of the displacement at $t=0$ is,

  $a=-30$

The value of $2m$ is,

  $\begin{array}{l}2m=80\\ m=40\end{array}$

The damping factor is,

  $b=0.6$

(b)

To determine

To find: The initial displacement of the bob.

Answer to Problem 29AYU

The initial displacement is $a=-30$ to the left.

Explanation of Solution

Given:

The given covered by the bob is $d=-30e^{\frac{-0.6t}{80}}\cos \left(\sqrt{{\left(\frac{2\pi }{7}\right)}^2-\frac{0.36}{6400}t}\right)$ .

Calculation:

Consider the given equation for distance is,

  $d=-30e^{\frac{-0.6t}{80}}\cos \left(\sqrt{{\left(\frac{2\pi }{7}\right)}^2-\frac{0.36}{6400}t}\right)$

From above the initial displacement of the bob is,

  $a=-30$

The initial displacement is $a=-30$ to the left.

(c)

To determine

To find: The graph of the motion.

Answer to Problem 29AYU

The required diagram is shown in Figure 1

Explanation of Solution

Given:

The given covered by the bob is $d=-30e^{\frac{-0.6t}{80}}\cos \left(\sqrt{{\left(\frac{2\pi }{7}\right)}^2-\frac{0.36}{6400}t}\right)$ .

Calculation:

Consider the given equation for distance is,

  $d=-30e^{\frac{-0.6t}{80}}\cos \left(\sqrt{{\left(\frac{2\pi }{7}\right)}^2-\frac{0.36}{6400}t}\right)$

By the use of MAPPLE, the graph of $d\left(t\right)$ is shown in Figure 1

  

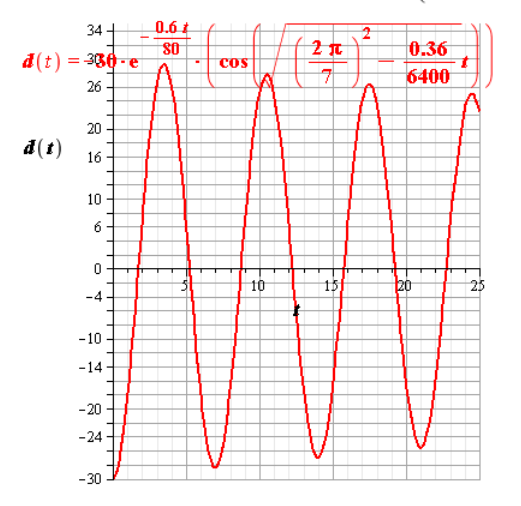
Figure 1

(d)

To determine

To find: The displacement of the bob at the start of the second oscillation.

Answer to Problem 29AYU

Thestart of the second oscillation is approximately $28.5\text{m}$ to the left.

Explanation of Solution

Given:

The given covered by the bob is $d=-30e^{\frac{-0.6t}{80}}\cos \left(\sqrt{{\left(\frac{2\pi }{7}\right)}^2-\frac{0.36}{6400}t}\right)$ .

Calculation:

Consider the given equation for distance is,

  $d=-30e^{\frac{-0.6t}{80}}\cos \left(\sqrt{{\left(\frac{2\pi }{7}\right)}^2-\frac{0.36}{6400}t}\right)$

From the graph shown in Figure 1, the displacement of the graph at the start of the second oscillation is approximately $28.5\text{m}$ to the left.

(e)

To determine

To find: The displacement of the bob as the time increases without bound.

Answer to Problem 29AYU

The displacement of the bob as the time increases without bound reduces to zero.

Explanation of Solution

Given:

The given covered by the bob is $d=-30e^{\frac{-0.6t}{80}}\cos \left(\sqrt{{\left(\frac{2\pi }{7}\right)}^2-\frac{0.36}{6400}t}\right)$ .

Calculation:

Consider the given equation for distance is,

  $d=-30e^{\frac{-0.6t}{80}}\cos \left(\sqrt{{\left(\frac{2\pi }{7}\right)}^2-\frac{0.36}{6400}t}\right)$

From the graph is shown in Figure 1, as $t$ increases without bound $t\to \infty$ . The value of $e^{-\frac{0.6t}{80}}\to 0$ . The displacement of the object approaches zero $d\to 0$ .