
Concept explainers
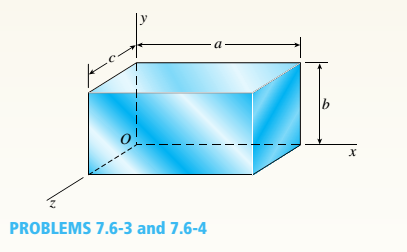
Solve the preceding problem if the element
is steel (E = 200 GPa. p = 0.30) with dimensions
a = 300 mm. h = 150 mm. and c = 150 mm a n d
with the stresses (T( = —62 MPa, r. = -45 MPa,
and = MPa.
For part (e) of Problem 7.6-3, find the maximum value of u. if the change in volume must be limited to —0.028%. For part (0. find the required value of if the strain energy must be 60 J.
(a)
The maximum shear stress in the material.
Answer to Problem 7.6.4P
The maximum shear stress on the material is
Explanation of Solution
Given information:
The element of length
Explanation:
Write the expression for the maximum shear stress.
Here, the maximum shear stress is
Calculation:
Since no shear stresses act on the parallelepiped,
Substitute,
Conclusion:
The maximum shear stress on the material is
(b)
The changes in the dimensions of the element.
Answer to Problem 7.6.4P
The change in length is
The change in height is
The change in width is
Explanation of Solution
Write the expression for the strain along
Here, the strain in the
Write the expression for strain in
Here, the strain in
Write the expression for strain in
Here, the strain in
Write the expression for the change in length.
Here, the length of element is
Write the expression for change in height.
Here, the height of element is
Write the expression for the change in width.
Here, the width of the element is
Calculation:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Conclusion:
The change in length is
The change in height is
The change in width is
(c)
The change in the volume of the element.
Answer to Problem 7.6.4P
The change in the volume is
Explanation of Solution
Write the expression for the change in the volume.
Here, the change in volume is
Write the expression for the volume.
Calculation:
Substitute
Substitute
Conclusion:
The change in the volume is
(d)
The strain energy stored in the element.
Answer to Problem 7.6.4P
The strain energy stored in the element is
Explanation of Solution
Write the expression for the strain energy.
Here, the strain energy is
Calculation:
Substitute
Conclusion:
The strain energy stored in the element is
(e)
The maximum value of normal stress along the
Answer to Problem 7.6.4P
The maximum value of normal stress along the
Explanation of Solution
Given information:
The change in volume is limited to
Explanation:
Write the expression for the change in volume.
Calculation:
Substitute
Conclusion:
The maximum value of normal stress along the
(f)
The required value of normal stress along the
Answer to Problem 7.6.4P
The required value of the normal stress along the
Explanation of Solution
Given information:
The strain energy of the system is
Explanation:
Write the expression for the strain energy in terms of stresses using Hooke’s law.
Calculation:
Substitute
Now solve the quadratic equation for obtaining the value of
Taking the negative sign.
Conclusion:
The required value of the normal stress along the
Want to see more full solutions like this?
Chapter 7 Solutions
Mechanics of Materials (MindTap Course List)
- The stresses acting on element B on the web of a train rail (see figure part a of Problem 7.2-5) arc found to be 5700 psi in compression in the horizontal direction and 2300 psi in compression in the vertical direction (see figure). Also, shear stresses of magnitude 2500 psi act in the directions shown. Determine the stresses acting on an element oriented at a counterclockwise angle of 50° from the horizontal. Show these stresses on a sketch of an element oriented at this angle.arrow_forward-11 A solid steel bar (G = 11.8 X 106 psi ) of diameter d = 2,0 in. is subjected to torques T = 8.0 kip-in. acting in the directions shown in the figure. Determine the maximum shear, tensile, and compressive stresses in the bar and show these stresses on sketches of properly oriented stress elements. Determine the corresponding maximum strains (shear, tensile, and compressive) in the bar and show these strains on sketches of the deformed elements.arrow_forwardSolve the preceding problem if the stresses acting on element A on the web of a train rail (see figure part a of Problem 7.2-5) are found to be 40 MPa in tension in the horizontal direction and 160 MPa in compression in the vertical direction. Also. shear stresses of magnitude 54 MPa act in the direct ions shown in the figure. Determine the stresses acting on an element oriented at a counterclockwise angle of 520 from the horizontal. Show these stresses on a sketch of an element oriented at this angle.arrow_forward
- A single steel strut AB with a diameter (a) Find the strut force Fs and average normal stress ds= 8 mm supports the vehicle engine hood of a in the strut. mass 20 kg that pivots about hinges at C and D (see (b) Find the average shear stress t aver in the bolt at A,figure parts a and b). The strut is bent into a loop at (C) Find the average bearing stress bon the bolt at A. its end and then attached to a bolt at A with a diameter db= 10 mm. Strut AB lies in a vertical plane.arrow_forwardPlastic bar of diameter d = 32 mm is compressed in a testing device by a Force P = 190 N that is applied as shown in the figure. (a) Determine the normal and shear stresses acting: on all faces of stress elements oriented at (1 ) an angle 8 = 00, (2) an angle ?? = 22.5s, and (3) an angle ?? = 45°. In each case, show the stresses on a sketch of a properly oriented element. What are smaxtmax (b) Find smax and tmax in the plastic bar if a re-cantering spring of stiffness k is inserted into the testing device, as shown in the figure. The spring stillness is 1/6 of the axial stiffness of the plastic bar.arrow_forwardRepeat the preceding problem but now find the stress state on Element A at the base. Let W%= 240 N, WL= 250 N, / = 5 mm, d = 360 mm. See the figure for the locations of clement A and all loadsarrow_forward
- An element in plane stress is subjected to stresses sx= -5500 psi, sy= -2000 psi, and Tx. = 1900 psi (see the figure for Problem 7.3-1). Determine the principal stresses and show them on a sketch of a properly oriented element.arrow_forwardA solid aluminum bar (G = 27 GPa ) of diameter d = 40 mm is subjected to torques T = 300 N - m acting in the directions shown in the figure, Determine the maximum shear, tensile, and compressive stresses in the bar and show these stresses on sketches of properly oriented stress elements. Determine the corresponding maximum strains (shear, tensile, and compressive) in the bar and show these strains on sketches of the deformed elements.arrow_forwardA steel hanger bracket ABCD has a solid, circular cross section with a diameter of d = 2 in. The dimension variable is b = 6 in. (see figure). Load P = 1200 lb is applied at D along a line DIh the coordinates of point H arc (8/>, — 5b, 2b), Find normal and shear stresses on a plane stress element on the surface of the bracket at A. Then find the principal stresses and maximum shear stress. Show each stress state on properly rotated elementsarrow_forward
- Repeat Problem 8.5-22 but replace the square tube column with a circular tube having a wall thickness r = 5 mm and the same cross-sectional area (3900 mm2) as that of the square tube in figure b in Problem 8.5-22. Also, add force P. = 120 N at B (a) Find the state of plane stress at C. (b) Find maximum normal stresses and show them on a sketch of a properly oriented element. (c) Find maximum shear stresses and show them on a sketch of a properly oriented element.arrow_forwardThe Force in the brake cable of the V-brake system shown in the figure is T — 45 lb. The pivot pin at A has a diameter d. = 0.25 in. and length L„ = 5/S in. Use the dimensions shown in the figure. Neglect the weight of the brake system. (a) Find the average shear stress rjm in the pivot pin where it is anchored to the bicycle frame at B. (b) Find the average bearing stress raverin the pivot pin over segment AB. (a) Find support reactions at A and B. (b) Find the resultant force in the shoe boll at A. (c) Find maximum average shear T and bearing AB stresses in the shoe bolt at A.arrow_forwardThe normal and shear stresses acting on element B are ??x= -46 MPa, sy= -13 MPa, and txy= 21 MPa (see figure for Problem 7.2-10). Determine the maximum shear stresses and associated normal stresses and show them on a sketch of a properly oriented element.arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
