
Concept explainers
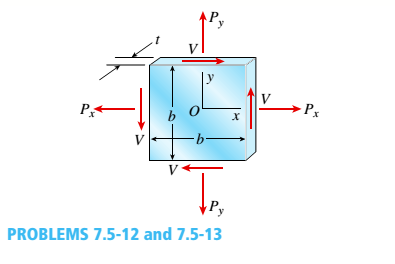
-12 A square plate of a width h and thickness t is Loaded by normal forces Pxand P and by shear forces V, as shown in the figure. These forces produce uniformly distributed stresses acting on the side faces of the plate.
(a) Calculate the change AV in the volume of the plate and the strain energy U stored in the plate if the dimensions are ft = 600 mm and f = 40 mm; the plate is made of magnesium with E = 41 GPa and v = 0,35; and the forces are Pv= 420 kN, P, = 210 kN, and V = 96 kN. (b) Find the maximum permissible thickness of the plate when the strain energy U must be at least 62 J. [Assume that all other numerical values in part (a) are unchanged.]
(c) Find the minimum width b of the square plate of thickness / = 40 mm when the change in volume of the plate cannot exceed 0.018% of the original volume.
(a)
The change
The strain energy
Answer to Problem 7.5.12P
The change
The strain energy
Explanation of Solution
Given information:
The normal force acting on the x-direction is
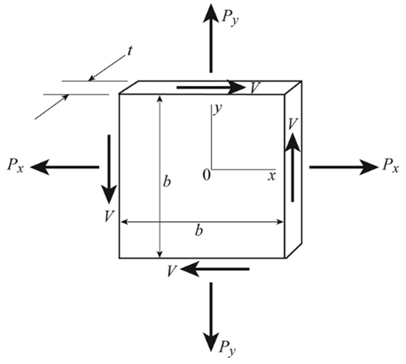
Figure (1)
Write the expression for the volumetric strain.
Here, the change in the volume of the plate is
Write the expression for the strain energy stored in the plate.
Here, the strain energy stored in the plate is
Write the expression of the original volume of plate
Here, the width of the plate is
Write the expression for the stress along x-direction.
Here the normal force along x-direction is
Write the expression for the stress along y-direction.
Here the normal force along y-direction is
Write the expression for the area of the plate.
Write the expression for the shear modulus.
Write the expression of the volumetric strain.
In the following plate we have two surface area at which shear force is applied so, the surface area for the shear stress is
Write the expression of the shear stress.
Calculation:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Conclusion:
The change
The strain energy
(b)
The maximum permissible thickness of the plate.
Answer to Problem 7.5.12P
The maximum permissible thickness of the plate is
Explanation of Solution
Given information:
The strain energy
Write the expression of the strain energy stored in the plate.
Calculation:
Substitute
Conclusion:
The maximum permissible thickness of the plate is
(c)
The minimum width
Answer to Problem 7.5.12P
The minimum width
Explanation of Solution
Given information:
The thickness of square plate is
Write the expression of the condition of the change in the length.
Calculation:
Substitute
Substitute
Substitute
Conclusion: The minimum width
Want to see more full solutions like this?
Chapter 7 Solutions
Mechanics of Materials (MindTap Course List)
- Question 5. The diagram below shows a mass suspended from a tie supported by two horizontal braces of equal length. The tie forms an angle "a" of 60° to the horizontal plane, the braces form an angle 0 of 50° to the vertical plane. If the mass suspended is 10 tonnes, and the braces are 10m long, find: a) the force in the tie; & b) the force in the braces Horizontal Braces, Tie Massarrow_forward= MMB 241 Tutorial 2.pdf 1 / 3 75% + + Tutorial z Topic: Kinematics of Particles:-. QUESTIONS 1. Use the chain-rule and find y and ŷ in terms of x, x and x if a) y=4x² b) y=3e c) y = 6 sin x 2. The particle travels from A to B. Identify the three unknowns, and write the three equations needed to solve for them. 8 m 10 m/s 30° B x 3. The particle travels from A to B. Identify the three unknowns, and write the three equations needed to solve for them. A 40 m/s 20 m B 1arrow_forward3 m³/s- 1 md 45° V 1.8 mr 2mrarrow_forward
- = MMB 241 Tutorial 2.pdf 3/3 75% + + 6. A particle is traveling along the parabolic path y = 0.25 x². If x = 8 m, vx=8 m/s, and ax= 4 m/s² when t = 2 s, determine the magnitude of the particle's velocity and acceleration at this instant. y = 0.25x² -x 7. Determine the speed at which the basketball at A must be thrown at the angle of 30° so that it makes it to the basket at B. 30° -x 1.5 m B 3 m -10 m- 8. The basketball passed through the hoop even though it barely cleared the hands of the player B who attempted to block it. Neglecting the size of the ball, determine the 2arrow_forwardAdhesives distribute loads across the interface, whereas fasteners create areas of localized stresses. True or Falsearrow_forwardA continuous column flash system is separating 100 kmol/h of a saturated liquid feed that is 45 mol% methanol and 55 mol% water at 1.0 atm. Operate with L/V = 1.5 and the outlet bottoms at xN = 0.28. Find the values of FL, FV, y1, and the number of equilibrium stages required. Find the value of Q used to vaporize FV. For a normal flash with the same feed and the same V/F, find the values of x and y.arrow_forward
- A beer still is being used to separate ethanol from water at 1.0 atm. The saturated liquid feed flow rate is F = 840.0 kmol/h. The feed is 44.0 mol% ethanol. The saturated vapor steam is pure water with ratio of steam flow rate S to feed rate, S/F = 2/3. We desire a bottoms product that is 4.0 mol% ethanol. CMO is valid. Find the mole fraction of ethanol in the distillate vapor, yD,E. Find the number of equilibrium stages required. If the feed is unchanged and the S/F ratio is unchanged, but the number of stages is increased to a very large number, what is the lowest bottoms mole fraction of ethanol that can be obtained?arrow_forward3.1 Convert the following base-2 numbers to base-10: (a) 1011001, (b) 110.0101, and (c) 0.01011.arrow_forwardConsider the forces acting on the handle of the wrench in (Figure 1). a) Determine the moment of force F1={−F1={−2i+i+ 4 jj −−8k}lbk}lb about the zz axis. Express your answer in pound-inches to three significant figures. b) Determine the moment of force F2={F2={3i+i+ 7 jj −−6k}lbk}lb about the zz axis. Express your answer in pound-inches to three significant figures.arrow_forward
- I need you to explain each and every step (Use paper)arrow_forwardCalculate the Moment About the Point A -20"- 5 lb 40 N D 1.5 m 40 N 4.5 m A 15 lb. 150 mm 52 N 5 12 100 mm 15 lb. 26 lb. 12 5 34 lb. 13 8 15 77777 36 lb.arrow_forwardCalculate the Moment About the Point A -20"- 5 lb 40 N D 1.5 m 40 N 4.5 m A 15 lb. 150 mm 52 N 5 12 100 mm 15 lb. 26 lb. 12 5 34 lb. 13 8 15 77777 36 lb.arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
