
(a)
Interpretation:
The engineering stress-strain curve should be plotted and the 0.2 % offset yield strength should be calculated for the given data of polyvinyl chloride.
Concept Introduction:
The maximum amount of elastic deformation which is bearable by any material is defined as yield strength.
Answer to Problem 6.39P
The yield strength for 0.2% offset is 11,600 psi for a given sample of polyvinyl chloride.
Explanation of Solution
The tabular data providing details about the load and length difference for a given sample.
Let us calculate the stress for the sample with the help of below formula:
| Load (lb.) | |
| 0 | 0.00000 |
| 300 | 0.00746 |
| 600 | 0.01496 |
| 900 | 0.02374 |
| 1200 | 0.032 |
| 1500 | 0.046 |
| 1660 | 0.07 (maximum load) |
| 1600 | 0.094 |
| 1420 | 0.12 (fracture) |
For determining the strain of the a given sample,
With the use of a givenspreadsheet and applied loads, one can tabulate the engineering stress and strain as follows:
| Load (F) | Length ( | Change in length ( | Gage length | Stress ( | Strain ( |
| 0 | 2 | 0 | 2 | 0 | 0 |
| 300 | 2 | 0.00746 | 2.00746 | 2386.635 | 0.00373 |
| 600 | 2 | 0.01496 | 2.01496 | 4773.27 | 0.00748 |
| 900 | 2 | 0.02374 | 2.02374 | 7159.905 | 0.0.1187 |
| 1200 | 2 | 0.032 | 2.032 | 9546.539 | 0.016 |
| 1500 | 2 | 0.046 | 2.046 | 11933.17 | 0.023 |
| 1660 | 2 | 0.07 | 2.07 | 13206.05 | 0.035 |
| 1600 | 2 | 0.094 | 2.094 | 12728.72 | 0.047 |
| 1420 | 2 | 0.12 | 2.12 | 11296.74 | 0.06 |
Now, one can plot the stress-strain curve from the above gathered tabular data as below:
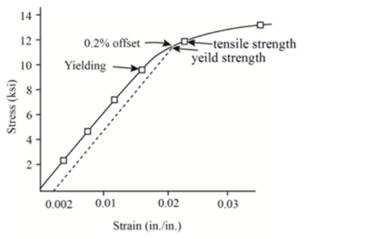
The above graph can provide the value of yield strength for 0.2% offset as 11,600 psi.
Therefore, polyvinyl chloride sample has the yield strength for 0.2% offset as 11,600 psi.
(b)
Interpretation:
With the help of plotted engineering stress-strain curve, the tensile strength should be calculated.
Concept Introduction:
Tensile strength can be defined as the measurement of maximum deformation which can be bearable by any material without undergoing necking condition.
Answer to Problem 6.39P
The tensile strength will be 12728.72 psi for a given sample of polyvinyl chloride.
Explanation of Solution
With the use of a givenspreadsheet and applied loads, one can tabulate the engineering stress and strain as below:
| Load (F) | Length ( | Change in length ( | Gage length | Stress ( | Strain ( |
| 0 | 2 | 0 | 2 | 0 | 0 |
| 300 | 2 | 0.00746 | 2.00746 | 2386.635 | 0.00373 |
| 600 | 2 | 0.01496 | 2.01496 | 4773.27 | 0.00748 |
| 900 | 2 | 0.02374 | 2.02374 | 7159.905 | 0.0.1187 |
| 1200 | 2 | 0.032 | 2.032 | 9546.539 | 0.016 |
| 1500 | 2 | 0.046 | 2.046 | 11933.17 | 0.023 |
| 1660 | 2 | 0.07 | 2.07 | 13206.05 | 0.035 |
| 1600 | 2 | 0.094 | 2.094 | 12728.72 | 0.047 |
| 1420 | 2 | 0.12 | 2.12 | 11296.74 | 0.06 |
Now, one can plot the stress-strain curve from the above gathered tabular data as below:
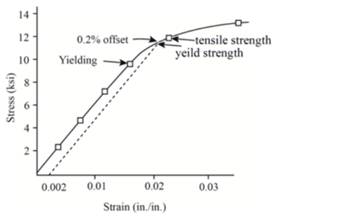
The above graph can provide the value of tensile strength as 12728.72 psi.
Therefore, the given sample of polyvinyl chloride has the tensile strength of12728.72 psi.
(c)
Interpretation:
With the help of plotted engineering stress-strain curve, the value of modulus of elasticity should be calculated.
Concept Introduction:
Modulus of elasticity is also known as coefficient of elasticity or elastic modulus and can be defined as the ratio of the stress in the a given object body to the corresponding strain.
Answer to Problem 6.39P
The value of modulus of elasticity is 603193 psi for give polyvinyl chloride.
Explanation of Solution
With the use of a givenspreadsheet and applied loads, one can tabulate the engineering stress and strain as below:
| Load (F) | Length ( | Change in length ( | Gage length | Stress ( | Strain ( |
| 0 | 2 | 0 | 2 | 0 | 0 |
| 300 | 2 | 0.00746 | 2.00746 | 2386.635 | 0.00373 |
| 600 | 2 | 0.01496 | 2.01496 | 4773.27 | 0.00748 |
| 900 | 2 | 0.02374 | 2.02374 | 7159.905 | 0.0.1187 |
| 1200 | 2 | 0.032 | 2.032 | 9546.539 | 0.016 |
| 1500 | 2 | 0.046 | 2.046 | 11933.17 | 0.023 |
| 1660 | 2 | 0.07 | 2.07 | 13206.05 | 0.035 |
| 1600 | 2 | 0.094 | 2.094 | 12728.72 | 0.047 |
| 1420 | 2 | 0.12 | 2.12 | 11296.74 | 0.06 |
Now, one can plot the stress-strain curve from the above gathered tabular data as below:
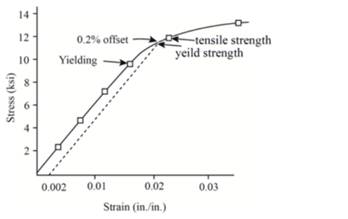
The formula of Hook's law can be used for calculating modulus of elasticity.
Therefore, the value of modulus of elasticity for given polyvinyl chloride is 603193 psi.
(d)
Interpretation:
With the help of plotted engineering stress-strain curve, the value of % elongation should be calculated.
Concept Introduction:
Elongation is defined as term used to determine the change in gauge length of any material when it is on static tension test.
Answer to Problem 6.39P
The value of % elongation is 4.5 % for a given polyvinyl chloride.
Explanation of Solution
With the use of a givenspreadsheet and applied loads, one can tabulate the engineering stress and strain as below:
| Load (F) | Length ( | Change in length ( | Gage length | Stress ( | Strain ( |
| 0 | 2 | 0 | 2 | 0 | 0 |
| 300 | 2 | 0.00746 | 2.00746 | 2386.635 | 0.00373 |
| 600 | 2 | 0.01496 | 2.01496 | 4773.27 | 0.00748 |
| 900 | 2 | 0.02374 | 2.02374 | 7159.905 | 0.0.1187 |
| 1200 | 2 | 0.032 | 2.032 | 9546.539 | 0.016 |
| 1500 | 2 | 0.046 | 2.046 | 11933.17 | 0.023 |
| 1660 | 2 | 0.07 | 2.07 | 13206.05 | 0.035 |
| 1600 | 2 | 0.094 | 2.094 | 12728.72 | 0.047 |
| 1420 | 2 | 0.12 | 2.12 | 11296.74 | 0.06 |
Now, one can plot the stress-strain curve from the above gathered tabular data as below:
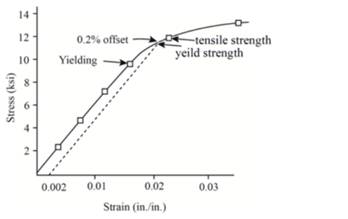
The following formula can be used to determine the value of % elongation.
Therefore, thevalue of % elongationis 4.5% for given polyvinyl chloride sample.
(e)
Interpretation:
With the help of plotted engineering stress-strain curve, the value of % reduction in area should be calculated.
Concept Introduction:
Reduction if area of any material is directly related to the reduction in cross-section area of the tensile test piece after fracture.
Answer to Problem 6.39P
The value of % reduction in area is 3.5 % for a given polyvinyl chloride.
Explanation of Solution
With the use of a givenspreadsheet and applied loads, one can tabulate the engineering stress and strain as below:
| Load (F) | Length ( | Change in length ( | Gage length | Stress ( | Strain ( |
| 0 | 2 | 0 | 2 | 0 | 0 |
| 300 | 2 | 0.00746 | 2.00746 | 2386.635 | 0.00373 |
| 600 | 2 | 0.01496 | 2.01496 | 4773.27 | 0.00748 |
| 900 | 2 | 0.02374 | 2.02374 | 7159.905 | 0.0.1187 |
| 1200 | 2 | 0.032 | 2.032 | 9546.539 | 0.016 |
| 1500 | 2 | 0.046 | 2.046 | 11933.17 | 0.023 |
| 1660 | 2 | 0.07 | 2.07 | 13206.05 | 0.035 |
| 1600 | 2 | 0.094 | 2.094 | 12728.72 | 0.047 |
| 1420 | 2 | 0.12 | 2.12 | 11296.74 | 0.06 |
Now, one can plot the stress-strain curve from the above gathered tabular data as below:
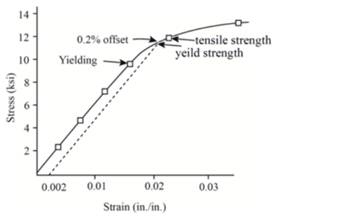
The following formula can be used to determine the value of % reduction in area.
Therefore, the given polyvinyl chloride sample carries 3.5% the value of % reduction in area.
(f)
Interpretation:
With the help of plotted engineering stress-strain curve, the engineering stress should be determined at fracture.
Concept Introduction:
Engineering stress is a term explained as a force or applied load on the a given object's cross-sectional area and it is also known as nominal stress.
Answer to Problem 6.39P
The engineering stress is 11,296.74 psi fora given polyvinyl chloride.
Explanation of Solution
With the use of a givenspreadsheet and applied loads, one can tabulate the engineering stress and strain as below:
| Load (F) | Length ( | Change in length ( | Gage length | Stress ( | Strain ( |
| 0 | 2 | 0 | 2 | 0 | 0 |
| 300 | 2 | 0.00746 | 2.00746 | 2386.635 | 0.00373 |
| 600 | 2 | 0.01496 | 2.01496 | 4773.27 | 0.00748 |
| 900 | 2 | 0.02374 | 2.02374 | 7159.905 | 0.0.1187 |
| 1200 | 2 | 0.032 | 2.032 | 9546.539 | 0.016 |
| 1500 | 2 | 0.046 | 2.046 | 11933.17 | 0.023 |
| 1660 | 2 | 0.07 | 2.07 | 13206.05 | 0.035 |
| 1600 | 2 | 0.094 | 2.094 | 12728.72 | 0.047 |
| 1420 | 2 | 0.12 | 2.12 | 11296.74 | 0.06 |
Now, one can plot the stress-strain curve from the above gathered tabular data as below:

Above graph is extended upto fracture strength as follows:
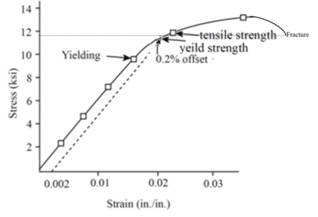
Therefore,the value of engineering stress will be 11,296.74 psi for a given polyvinyl chloride.
(g)
Interpretation:
With the help of plotted engineering stress-strain curve, the value of modulus of resilience should be determined.
Concept Introduction:
The amount of energy required to get absorbed by the material to return back to its original state is defined as resilience.
Modulus of resilience can be defined as the energy required by the material to return from its stress condition from zero to the yield stress limit.
Answer to Problem 6.39P
The value of modulus of resilience is 76.37 psi for a given polyvinyl chloride.
Explanation of Solution
With the use of a givenspreadsheet and applied loads, one can tabulate the engineering stress and strain as below:
| Load (F) | Length ( | Change in length ( | Gage length | Stress ( | Strain ( |
| 0 | 2 | 0 | 2 | 0 | 0 |
| 300 | 2 | 0.00746 | 2.00746 | 2386.635 | 0.00373 |
| 600 | 2 | 0.01496 | 2.01496 | 4773.27 | 0.00748 |
| 900 | 2 | 0.02374 | 2.02374 | 7159.905 | 0.0.1187 |
| 1200 | 2 | 0.032 | 2.032 | 9546.539 | 0.016 |
| 1500 | 2 | 0.046 | 2.046 | 11933.17 | 0.023 |
| 1660 | 2 | 0.07 | 2.07 | 13206.05 | 0.035 |
| 1600 | 2 | 0.094 | 2.094 | 12728.72 | 0.047 |
| 1420 | 2 | 0.12 | 2.12 | 11296.74 | 0.06 |
Now, one can plot the stress-strain curve from the above gathered tabular data as below:
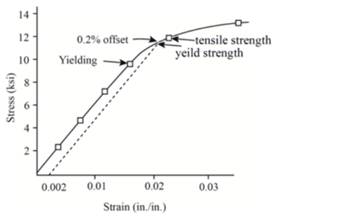
From the graph, the value of modulus of resilience is 9546.539 psi.
Now,
Therefore, the sample of polyvinyl chloride has 76.37 psi as the value of modulus of resilience.
Want to see more full solutions like this?
Chapter 6 Solutions
Essentials of Materials Science and Engineering, SI Edition
- plese solbe this problem and give the correct answer solve step by step find the forces and line actionarrow_forwardplease help me to solve this problems first write the line of action and them find the forces {fx=0: fy=0: mz=0: and them draw the shear and bending moment diagram. please explain step by steparrow_forwardplease solve this problem step by step like human and give correct answer step by steparrow_forward
- a) A 14-ft. tall and12-ft.-8-in. long fully grouted reinforced masonry wall is constructed of 8-in.CMU. It is to be analyzed for out-of-plane loading. Construct thenP -nM curves for the wallwith the following three vertical reinforcement scenarios: (1) 10 No. 6 bars at 16 in. spacing,(2) 10 No. 5 bars at 16 in. spacing, and (3) 7 No. 4 bars at 24 in. spacing. The steel is Grade60 with a modulus of elasticity of 29,000 ksi, and the masonry has a compressive strength of2,000 psi. You may use Excel or Matlab to construct the curves. Also, show the maximumnPallowed by the code for each case.(b) For each of the above reinforcement scenarios, determine the maximum axial loads that arepermitted for the tension-controlled condition and transition condition.(c) Discuss how the amount of vertical reinforcement affects thenPn - Mn curve.arrow_forwardPROBLEM 11: Determine the force, P, that must be exerted on the handles of the bolt cutter. (A) 7.5 N (B) 30.0 N (C) 52.5 N (D) 300 N (E) 325 N .B X 3 cm E 40 cm cm F = 1000 N 10 cm 3 cm boltarrow_forwardUsing the moment-area theorems, determine a) the rotation at A, b) the deflection at L/2, c) the deflection at L/4. (Hint: Use symmetry for Part a (θA= - θB, or θC=0), Use the rotation at A for Parts b and c. Note that all deformations in the scope of our topics are small deformation and for small θ, sinθ=θ).arrow_forward
- Distilled water is being cooled by a 20% propylene glycol solution in a 1-1/U counter flow plate and frame heat exchanger. The water enters the heat exchanger at 50°F at a flow rate of 86,000 lbm/h. For safety reasons, the water outlet temperature should never be colder than 35°F. The propylene glycol solution enters the heat exchanger at 28°F with a flow rate of 73,000 lbm/h. The port distances on the heat exchanger are Lv = 35 in and Lh = 18 in. The plate width is Lw = 21.5 2 in. The plate thickness is 0.04 in with a plate pitch of 0.12 in. The chevron angle is 30° and the plate enlargement factor is 1.17. All ports have a 2 in diameter. The fouling factor of the propylene glycol solution can be estimated as 2 ×10−5 h-ft2-°F/Btu. a. Determine the maximum number of plates the heat exchanger can have while ensuring that the water outlet temperature never drops below 35°F. b. Determine the thermal and hydraulic performance of the heat exchanger with the specified number of plates.…arrow_forwardLiquid pentane is flowing in the shell of a shell and tube heat exchanger at a rate of 350,000lbm/hr and an average temperature of 20°F. The shell has a diameter of 27 in and a length of 16ft. The tubes in the heat exchanger are ¾-in 15 BWG tubes on a 1-in triangular pitch. The purposeof this problem is to investigate how the number of baffles impacts the heat transfer and thepressure drop on the shell side of the heat exchanger. Calculate the shell-side convective heattransfer coefficient and pressure drop for the case where the heat exchanger has 10 baffles. Repeatthe calculation for 20 baffles. Then determine thea. Ratio of the shell-side convective heat transfer coefficient for the 20-baffle heat exchangerto the 10-baffle heat exchangerb. Ratio of the shell-side pressure drop for the 20-baffle heat exchanger to the 10-baffle heatexchangerc. If the optimum baffle spacing is somewhere between 0.4Ds and 0.6Ds, how many baffleswould you recommend for this heat exchanger? What are the…arrow_forwardCan you show why the answer is that for this question using second order differential equations, instead of laplace transformsarrow_forward
- I need help to solve the following case, thank youarrow_forwardIf you could help me answer these questions in matlab that would be great, I provided an additional picture detailing what the outcome should look like.arrow_forwardThe evaporator of a vapor compression refrigeration cycle utilizing R-123 as the refrigerant isbeing used to chill water. The evaporator is a shell and tube heat exchanger with the water flowingthrough the tubes. The water enters the heat exchanger at a temperature of 54°F. The approachtemperature difference of the evaporator is 3°R. The evaporating pressure of the refrigeration cycleis 4.8 psia and the condensing pressure is 75 psia. The refrigerant is flowing through the cycle witha flow rate of 18,000 lbm/hr. The R-123 leaves the evaporator as a saturated vapor and leaves thecondenser as a saturated liquid. Determine the following:a. The outlet temperature of the chilled waterb. The volumetric flow rate of the chilled water (gpm)c. The UA product of the evaporator (Btu/h-°F)d. The heat transfer rate between the refrigerant and the water (tons)arrow_forward
 MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage,
Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage, Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning
Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION
Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON
Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY
Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY





