
(a)
Interpretation:
The engineering stress-strain curve should be plotted and the 0.2 % offset yield strength should be calculated for the given data of magnesium.
Concept Introduction:
The maximum amount of elastic deformation which is bearable by any material is defined as yield strength.
Answer to Problem 6.40P
The yield strength for 0.2% offset is 185MPa for a given sample of magnesium.
Explanation of Solution
The tabular data providing details about the load and length difference for a given sample is as follows:
Calculate the engineering stress for the sample of with the help of below formula:
| Load (lb.) | |
| 0 | 0.00000 |
| 5000 | 0.0296 |
| 10,000 | 0.0592 |
| 15,00 | 0.0888 |
| 20,000 | 0.15 |
| 25,000 | 0.51 |
| 26,500 | 0.90 |
| 27,000 | 1.50 (fracture) |
| 26,500 | 2.10 |
| 25,000 | 2.79 (maximum load) |
In the equation (2), put value of F =5,000 N,
The below mentioned tabular data represent the value of engineering stress at different load applied at the given specimen of magnesium:
| F(N) | S (MPa) |
| 0 | 0 |
| 5000 | 44.20 |
| 10,000 | 88.40 |
| 15,00 | 132.60 |
| 20,000 | 176.80 |
| 25,000 | 221.04 |
| 26,500 | 234.30 |
| 27,000 | 238.72 |
| 26,500 | 234.30 |
| 25,000 | 221.04 |
Calculate the engineering strain for the sample of with the help of below formula:
The below mentioned tabular data represent the value of engineering stress at different load applied at the given specimen of magnesium:
| e (cm/cm) | |
| 0.00000 | 0 |
| 0.0296 | |
| 0.0592 | |
| 0.0888 | |
| 0.15 | |
| 0.51 | 0.017 |
| 0.90 | 0.030 |
| 1.50 | 0.050 |
| 2.10 | 0.070 |
| 2.79 | 0.093 |
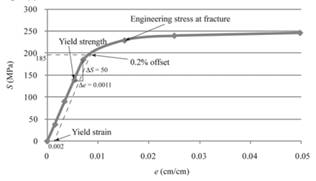
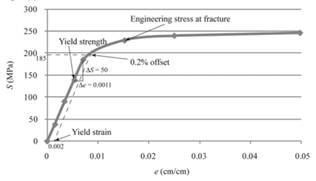
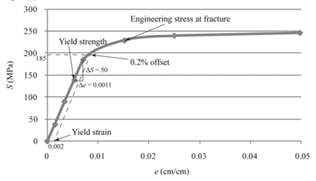
With the use of given both spread sheets, one can tabulate the engineering stress and strain curve as follows:
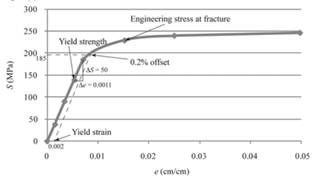
The above graph can provide the value of yield strength for 0.2% offset as 185 MPa.
Therefore, one can conclude that magnesium sample contains the yield strength for 0.2% offset as 185MPa.
(b)
Interpretation:
With the help of plotted engineering stress-strain curve, the tensile strength should be calculated.
Concept Introduction:
The tensile strength can be defined as the measurement of maximum deformation which can be bearable by any material without undergoing necking condition.
Answer to Problem 6.40P
The tensile strength is 239 MPa for a given sample of magnesium.
Explanation of Solution
With the use of a given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as follows:
| F(N) | S (MPa) | e (cm/cm) | |
| 0 | 0 | 0.00000 | 0 |
| 5000 | 44.20 | 0.0296 | |
| 10,000 | 88.40 | 0.0592 | |
| 15,00 | 132.60 | 0.0888 | |
| 20,000 | 176.80 | 0.15 | |
| 25,000 | 221.04 | 0.51 | 0.017 |
| 26,500 | 234.30 | 0.90 | 0.030 |
| 27,000 | 238.72 | 1.50 | 0.050 |
| 26,500 | 234.30 | 2.10 | 0.070 |
| 25,000 | 221.04 | 2.79 | 0.093 |
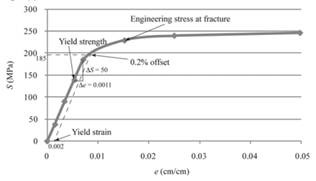
The tensile strength can be determined by use of below mentioned formula:
Therefore, one can conclude that the given sample of magnesium has the tensile strength of 239 MPa.
(c)
Interpretation:
With the help of plotted engineering stress-strain curve, the value of modulus of elasticity should be calculated.
Concept Introduction:
Modulus of elasticity is also known as coefficient of elasticity or elastic modulus and can be defined as the ratio of the stress in the given object body to the corresponding strain.
Answer to Problem 6.40P
The value of modulus of elasticity is 45,455 MPa for a given magnesium.
Explanation of Solution
With the use of a given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as follows:
| F(N) | S (MPa) | e (cm/cm) | |
| 0 | 0 | 0.00000 | 0 |
| 5000 | 44.20 | 0.0296 | |
| 10,000 | 88.40 | 0.0592 | |
| 15,00 | 132.60 | 0.0888 | |
| 20,000 | 176.80 | 0.15 | |
| 25,000 | 221.04 | 0.51 | 0.017 |
| 26,500 | 234.30 | 0.90 | 0.030 |
| 27,000 | 238.72 | 1.50 | 0.050 |
| 26,500 | 234.30 | 2.10 | 0.070 |
| 25,000 | 221.04 | 2.79 | 0.093 |
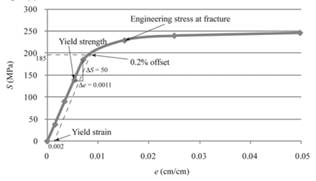
The modulus of elasticity can be determined by use of below mentioned formula:
In above equation,
Therefore, the value of modulus of elasticity for given magnesium is 45,455 MPa.
(d)
Interpretation:
With the help of plotted engineering stress-strain curve, the value of % elongation should be calculated.
Concept Introduction:
Elongation is defined as term used to determine the change in gauge length of any material when it is on static tension test.
Answer to Problem 6.40P
The value of % elongation is 8.7% for a given magnesium.
Explanation of Solution
With the use of a given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as follows:
| F(N) | S (MPa) | e (cm/cm) | |
| 0 | 0 | 0.00000 | 0 |
| 5000 | 44.20 | 0.0296 | |
| 10,000 | 88.40 | 0.0592 | |
| 15,00 | 132.60 | 0.0888 | |
| 20,000 | 176.80 | 0.15 | |
| 25,000 | 221.04 | 0.51 | 0.017 |
| 26,500 | 234.30 | 0.90 | 0.030 |
| 27,000 | 238.72 | 1.50 | 0.050 |
| 26,500 | 234.30 | 2.10 | 0.070 |
| 25,000 | 221.04 | 2.79 | 0.093 |
The following formula is used for determining the value of % elongation.
Therefore, the value of % elongation is 8.7% for given magnesium sample.
(e)
Interpretation:
With the help of plotted engineering stress-strain curve, the value of % reduction in area should be calculated.
Concept Introduction:
Reduction if area of any material is directly related to the reduction in cross-section area of the tensile test piece after fracture.
Answer to Problem 6.40P
The value of % reduction in area is 4.3% for given magnesium.
Explanation of Solution
With the use of given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as follows:
| F(N) | S (MPa) | e (cm/cm) | |
| 0 | 0 | 0.00000 | 0 |
| 5000 | 44.20 | 0.0296 | |
| 10,000 | 88.40 | 0.0592 | |
| 15,00 | 132.60 | 0.0888 | |
| 20,000 | 176.80 | 0.15 | |
| 25,000 | 221.04 | 0.51 | 0.017 |
| 26,500 | 234.30 | 0.90 | 0.030 |
| 27,000 | 238.72 | 1.50 | 0.050 |
| 26,500 | 234.30 | 2.10 | 0.070 |
| 25,000 | 221.04 | 2.79 | 0.093 |
One can use the following formula for determining the value of % reduction in area.
Therefore, the given magnesium sample carries 4.3% the value of % reduction in area.
(f)
Interpretation:
With the help of plotted engineering stress-strain curve, the true stress should be determined at necking.
Concept Introduction:
True stress can be defined as the applied force or load that is divided by the cross-sectional area of specimen or object. It can be also defined as the required amount of force that tends to deformation of specimen.
Answer to Problem 6.40P
The trues stress is 251 MPa for given magnesium at necking.
Explanation of Solution
With the use of given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as follows:
| F(N) | S (MPa) | e (cm/cm) | |
| 0 | 0 | 0.00000 | 0 |
| 5000 | 44.20 | 0.0296 | |
| 10,000 | 88.40 | 0.0592 | |
| 15,00 | 132.60 | 0.0888 | |
| 20,000 | 176.80 | 0.15 | |
| 25,000 | 221.04 | 0.51 | 0.017 |
| 26,500 | 234.30 | 0.90 | 0.030 |
| 27,000 | 238.72 | 1.50 | 0.050 |
| 26,500 | 234.30 | 2.10 | 0.070 |
| 25,000 | 221.04 | 2.79 | 0.093 |
The true stress at necking can be calculated with the use of below mentioned formula:
In the above equation, putting the values to determine true stress as below.
Therefore, the given sample of magnesium has 251 MPa as a trues stress value at necking.
(g)
Interpretation:
With the help of plotted engineering stress-strain curve, the value of modulus of resilience should be determined.
Concept Introduction:
The amount of energy required to get absorbed by the material to return back to its original state is defined as resilience.
Modulus of resilience can be defined as the energy required by the material to return from its stress condition from zero to the yield stress limit.
Answer to Problem 6.40P
The value of modulus of resilience is 0.132 MPa of given magnesium.
Explanation of Solution
With the use of given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as below:
| F(N) | S (MPa) | e (cm/cm) | |
| 0 | 0 | 0.00000 | 0 |
| 5000 | 44.20 | 0.0296 | |
| 10,000 | 88.40 | 0.0592 | |
| 15,00 | 132.60 | 0.0888 | |
| 20,000 | 176.80 | 0.15 | |
| 25,000 | 221.04 | 0.51 | 0.017 |
| 26,500 | 234.30 | 0.90 | 0.030 |
| 27,000 | 238.72 | 1.50 | 0.050 |
| 26,500 | 234.30 | 2.10 | 0.070 |
| 25,000 | 221.04 | 2.79 | 0.093 |
The value of yield strength and strain is 132 MPa and 0.002 respectively.
Therefore, the sample of magnesium has 0.132 MPa as the value of modulus of resilience.
Want to see more full solutions like this?
Chapter 6 Solutions
Essentials of Materials Science and Engineering, SI Edition
- Q11arrow_forwardMethyl alcohol at 25°C (ρ = 789 kg/m³, μ = 5.6 × 10-4 kg/m∙s) flows through the system below at a rate of 0.015 m³/s. Fluid enters the suction line from reservoir 1 (left) through a sharp-edged inlet. The suction line is 10 cm commercial steel pipe, 15 m long. Flow passes through a pump with efficiency of 76%. Flow is discharged from the pump into a 5 cm line, through a fully open globe valve and a standard smooth threaded 90° elbow before reaching a long, straight discharge line. The discharge line is 5 cm commercial steel pipe, 200 m long. Flow then passes a second standard smooth threaded 90° elbow before discharging through a sharp-edged exit to reservoir 2 (right). Pipe lengths between the pump and valve, and connecting the second elbow to the exit are negligibly short compared to the suction and discharge lines. Volumes of reservoirs 1 and 2 are large compared to volumes extracted or supplied by the suction and discharge lines. Calculate the power that must be supplied to the…arrow_forwardQ15arrow_forward
- 2) The transistor parameters of the NMOS device in the common-gate amplifier in Figure 2 are VTN = 0.4V, K'n = 100 μA / V², and λ=0. (50 points) a) Find RD such that VDSQ = VDs (sat) + 0.25V. b) Determine the transistor W/L ratio such that the small-signal voltage gain is Av=6. c) What is the value of VGSQ? Сс 2 mA Rp T V=-1.8 V V+= 1.8 V Figure 2arrow_forwardAnswer the question fully and accurately by providing the required files(Java Code, Two output files and written answers to questions 1-3 in a word document)meaning question 1 to 3 also provide correct answers for those questions.(note: this quetion is not graded).arrow_forwardcan you help me figure out the calculations so that i can input into autocad? Not apart of a graded assinment. Just a problem in class that i missed.arrow_forward
- Calculate the percent voltage regulation for a three-phase wye-connected 2500 kVA 6600-V turboalternator operating at full-load Unity power factor The per phase synchronous reactance and the armature resistance are 10.4 2 and 0.071 ≤2, respectively?arrow_forwardConsider a glass window (Hight = 1.2 m, Width = 2 m). The room thatfaces the window are maintained at 25 o C. The average temperature ofthe inner surface of the window is 5 o C. Calculate the total heat transferrate from through the window a) IdenCfy what type(s) of convecCon is important (circle one). • external forced (Chapter 7)• internal forced (Chapter 8)• natural convecCon (Chapter 9)• boiling and condensaCon (Chapter 10)b) IdenCfy the necessary equaCon(s) needed to solve the problem. c) IdenCfy important fluid properCes you need to solve the problem. d) Calculate the total heat transferred.arrow_forwardWater is condensing on a square plate (0.5 m x 0.5 m) placed verCcally. If the desired rate ofcondensaCon is 0.016 kJ/s, determine the necessary surface temperature of the plate at atmosphericpressure. Assume the film temperature of 90 o C for evaluaCon of fluid properCes of water and thesurface temperature of 80 o C for the evaluaCon of modified latent heat of vaporizaConarrow_forward
 MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage,
Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage, Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning
Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION
Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON
Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY
Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY





