
(a)
Interpretation:
Value of Yield strength at
Concept introduction:
Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,
Stress is defined as the ratio of load per unit area. It is denoted by
Where,
P is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
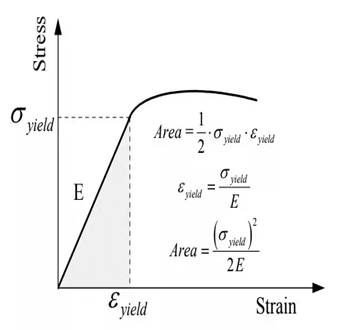
Offset is defined as the yield point in stress strain curve. The figure represents the Stress-Strain curve,
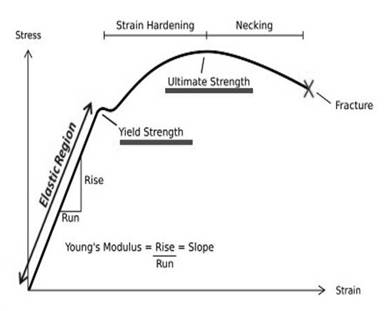
Answer to Problem 6.36P
The requiredvalue of Yield strength at
Explanation of Solution
Given information:
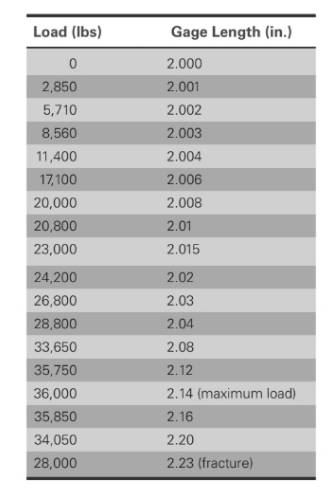
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
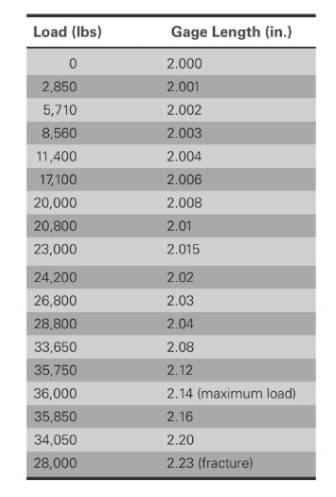
The values of load correspond to gage length is shown in table,
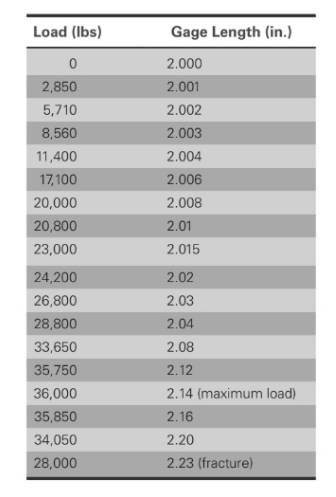
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
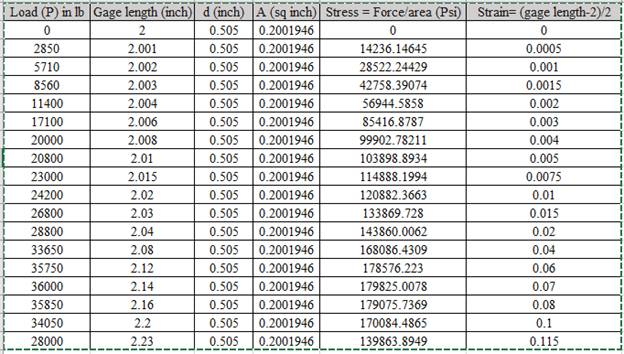
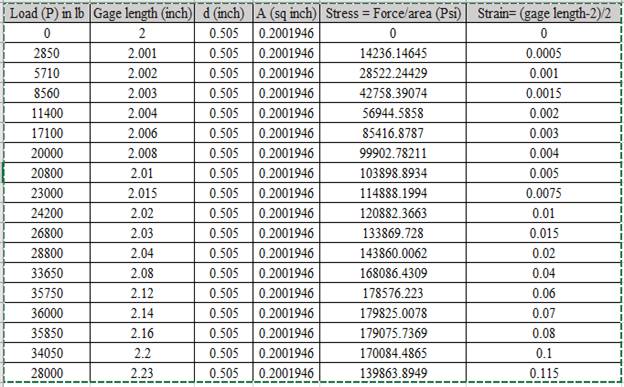
Calculation of stress and strain values are done using spreadsheet shown below,
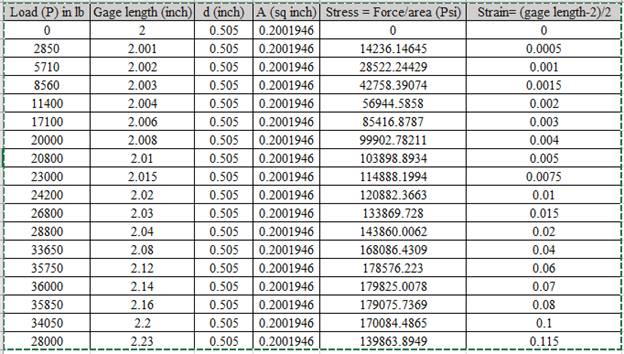
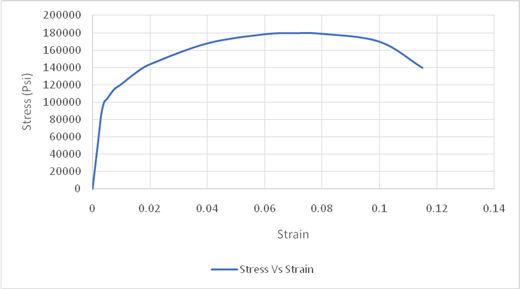
Using the data for Stress-Strain, Drawing the Stress Strain curve,
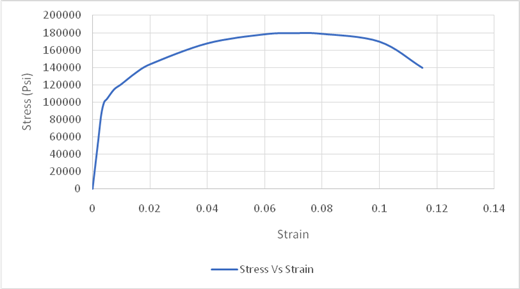
As, the value of offset is given in percentage so converting percentage by dividing it with
Drawing the tie line at offset of
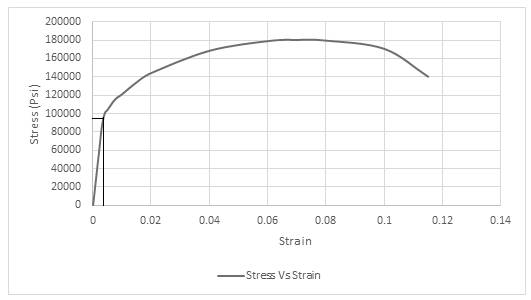
Thus, the required value of yield strength is
(b)
Interpretation:
The value of tensile strength for the given condition is to be determined.
Concept introduction:
Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
Tensile strength is the maximum load that material can withstand without rapture. The above graph is reflecting relationship between stress and strain.
Answer to Problem 6.36P
Thus, the required value of tensile strength is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
Calculation of stress and strain values are done using spreadsheet shown below,

Using the data for Stress-Strain, Drawing the Stress Strain curve,
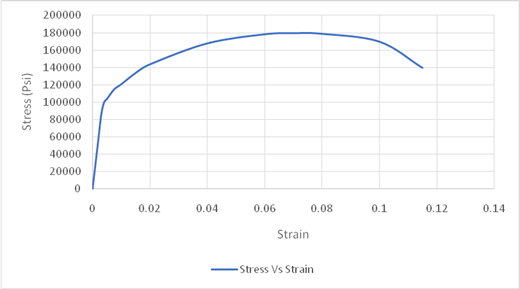
The maximum value of stress is used for obtaining the value of tensile strength. Drawing tie lines as shown in the figure below,
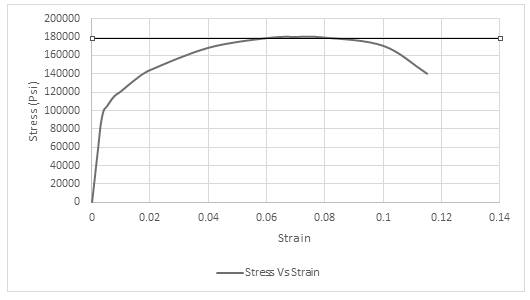
Thus, the required value of tensile strength is
(c)
Interpretation:
The value of Modulus of elasticity for the given condition should be calculated.
Concept introduction:
Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
The graph of Proportionality constant using modulus of elasticity,
Answer to Problem 6.36P
Thus, the required value of modulus of elasticity is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
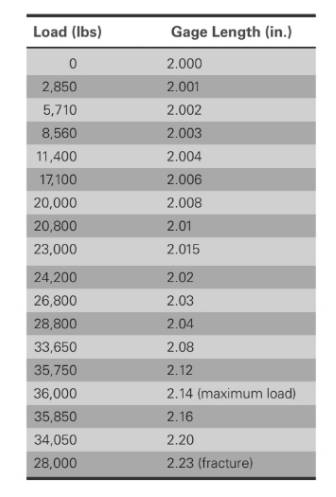
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
Calculation of stress and strain values are done using spreadsheet shown below,
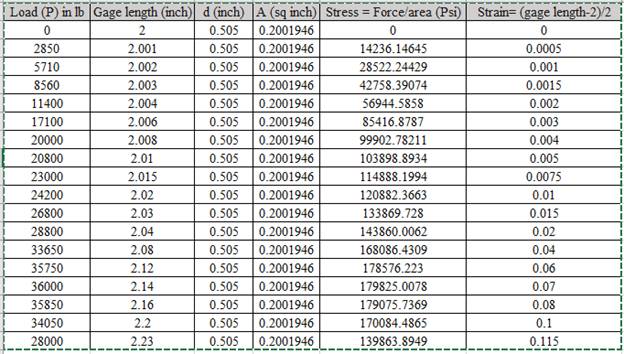
Using the data for Stress-Strain, Drawing the Stress Strain curve,
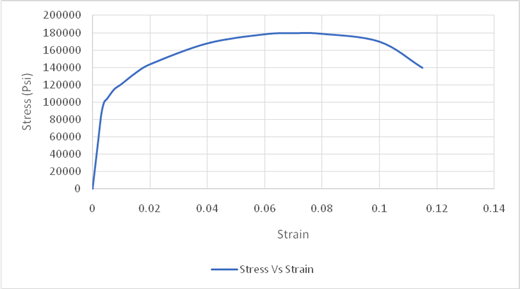
For calculating the modulus of elasticity, the values considered are highlighted in spreadsheet,
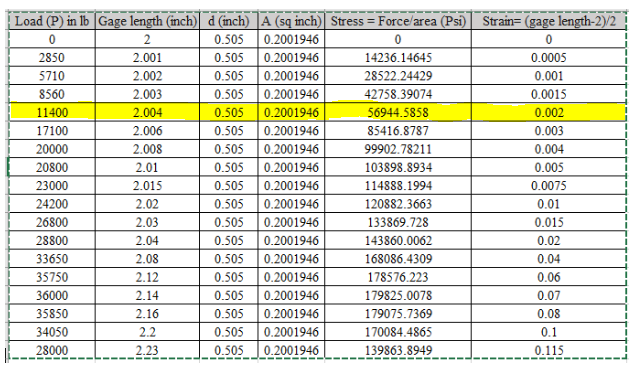
Using the above table the value of stress is
Calculation of modulus of elasticity,
Putting the values in formula,
Thus, the required value of modulus of elasticity is
(d)
Interpretation:
The value of percentage elongation for the given condition should be calculated.
Concept introduction:
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
Percentage elongation:
It is defined as the ratio of difference between final length and initial length to initial length. The relationship is given as,
Where,
Answer to Problem 6.36P
Thus, the required value of percentage elongation is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
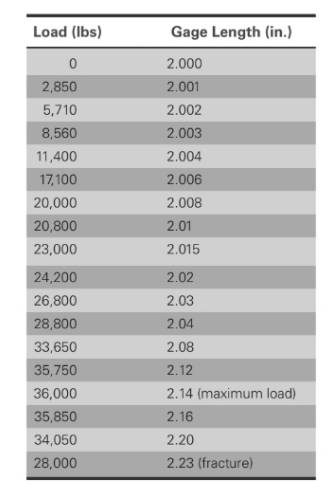
Based on the values,
Gage length before fracture is
Gage length after fracture is
Putting the values in the formula of percentage elongation,
Thus, the required value of percentage elongation is
(e)
Interpretation:
The value of percentage reduction in area for given condition should be calculated.
Concept introduction:
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
True Strain: It is defined as the ratio of gage length to instantaneous gage length. The formula is given below:
Where,
Percentage Reduction in Area:
It is defined as the ratio of difference between final length and initial length to initial length. The relationship is given as,
Where,
Answer to Problem 6.36P
The required value of percentage reduction in area is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
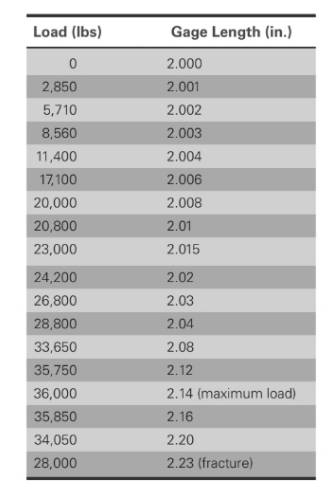
Based on the given values,
Calculation of
Calculation of
Substituting the values in the formula of percentage reduction of area,
The required value of percentage reduction in area is
(f)
Interpretation:
The value of engineering stress at fracture should be determined.
Concept introduction:
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
Answer to Problem 6.36P
Thus, the required value of Stress at fracture is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
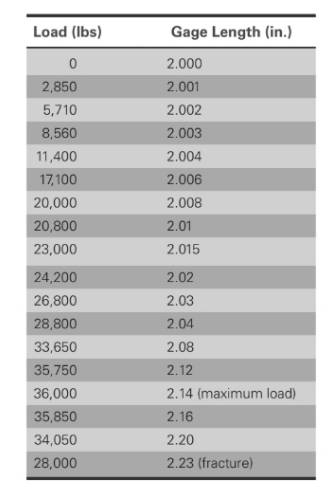
Based on the given values,
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
Calculation of stress and strain values are done using spreadsheet shown below,
Using the data for Stress-Strain, Drawing the Stress Strain curve,
Drawing the tie lie at the fracture point of Stress-Strain curve,
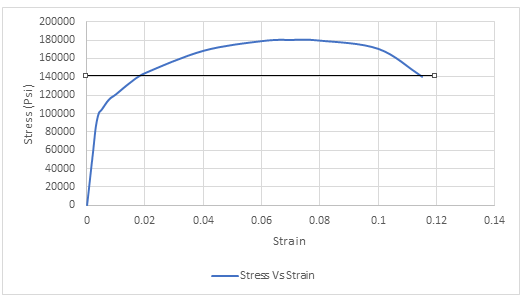
Thus, the required value of Stress at fracture is
(g)
Interpretation:
The value of true stress at necking should be calculated.
Concept introduction:
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
True stress is defined as the ratio of force per unit area. The relationship is given as,
Where,
Answer to Problem 6.36P
Thus, the required value of true stress at neck point is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
Based on the given values,
The different values of stress, Strain, gage diameter is shown below:
Calculation of true stress:
Following points are considered for calculating the values of true stress at gage length of
Calculation of area,
Calculation of strain,
Putting the values in the formula of true stress,
Thus, the required value of true stress at neck point is
(h)
Interpretation:
The value of Modulus of resilience for the given condition should be calculated.
Concept introduction:
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
Modulus of Resilience is defined as the maximum amount of energy that a material can withstand without creating the permanent distortion of the material.
The relationship of Modulus of Resilience is,
Where,
The graph is showing the values of yield stress and strain corresponding to the yield value,
Answer to Problem 6.36P
Thus, the required value of modulus of resilience is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
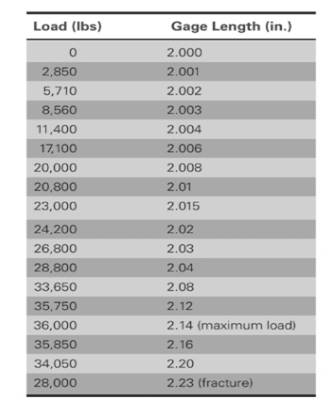
Based on the given values,
The different values of stress, Strain, gage diameter is shown below:
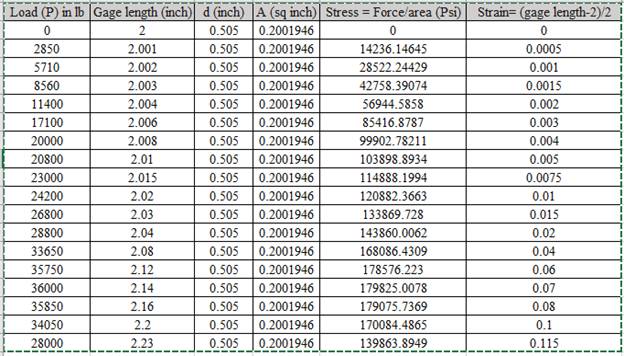
Based on the calculated values of stress and strain. The graph is shown below,
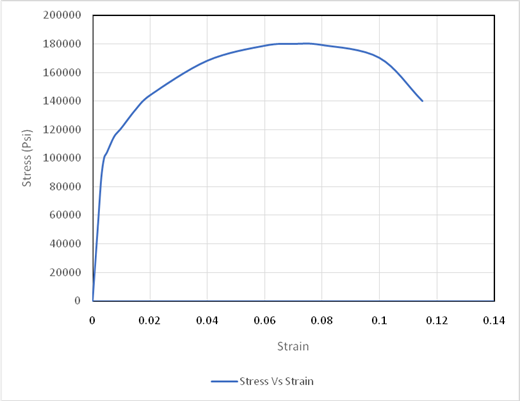
Using the above graph drawing tie lines,
Thus, based on the tie line, The value for yield stress is
Substituting the values for calculating the modulus of resilience,
Thus, the required value of modulus of resilience is
(i)
Interpretation:
The value of elastic and plastic strain corresponding to fracture should be determined.
Concept introduction:
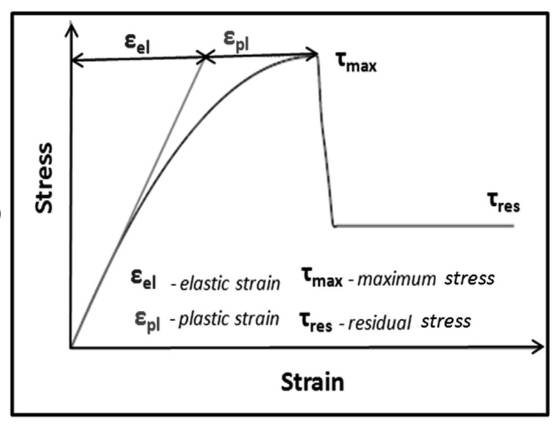
Elastic strainis defined as the distortion in the structure.
Plastic Strain is defined as the permanent distortion of structure.
The graph for elastic and plastic strain is shown below:
Answer to Problem 6.36P
Thus, the required value of elastic strain is
Thus, the required value of plastic strain is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
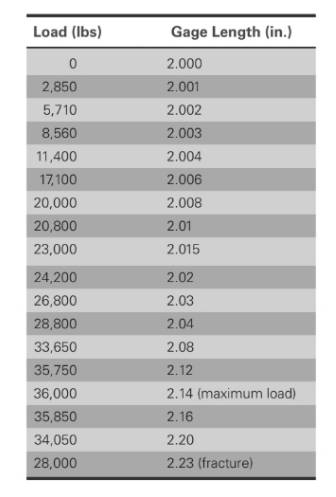
Based on the given values,
The different values of stress, Strain, gage diameter is shown below:
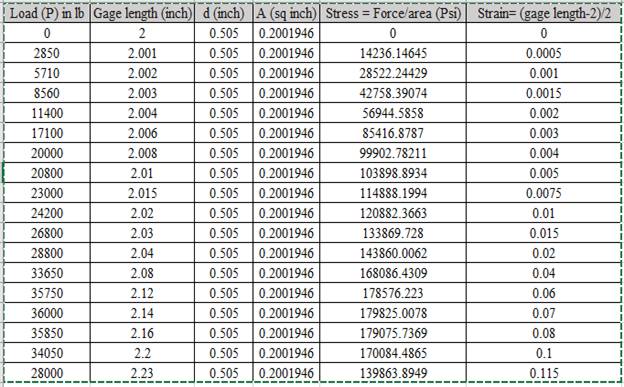
Based on the given values.
Plotting the graph,
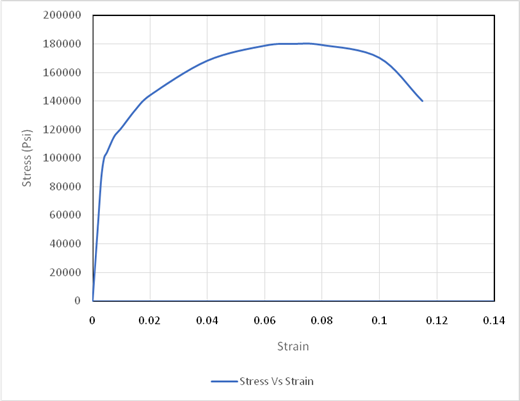
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
For calculating the modulus of elasticity, the values considered are highlighted in spreadsheet,
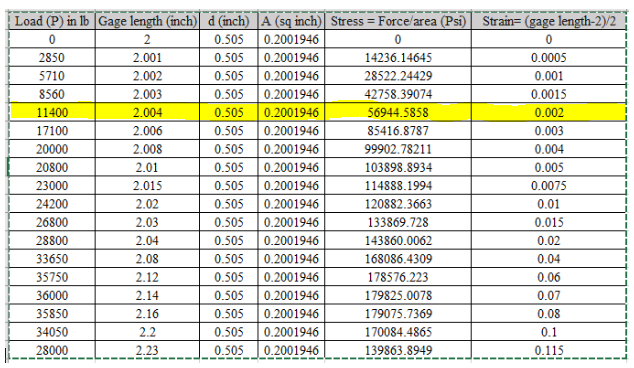
Using the above table the value of stress is
Putting the value of modulus of elasticity and stress,
Calculation of elastic strain,
Putting the values in formula,
Thus, the required value of elastic strain is
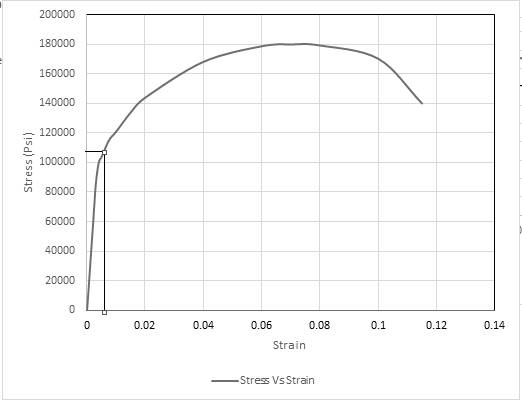
Using graph, drawing tie lines for determining the value of plastic strain,
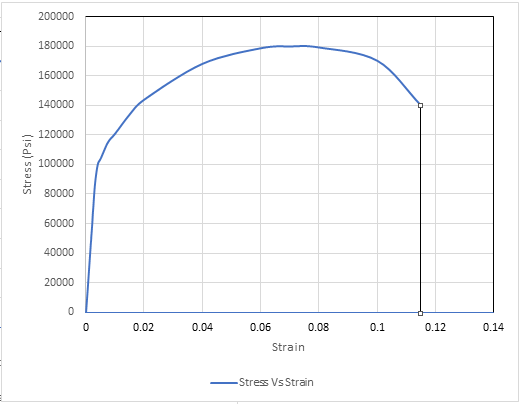
Thus, the required value of plastic strain is
(j)
Interpretation:
The transverse and axial strain for given condition should be determined. Also, the value of Poisson's ratio is to be calculated.
Concept introduction:
Transverse Strain is defined as the ratio of change in diameter to original diameter. The relationship is given as,
Where,
d is the original diameter.
Axial Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
Poisson's Ratio:
It is defined as the ratio of transverse strain to axial strain represented as:
Answer to Problem 6.36P
The required value of transverse strain is
Thus, the required value of axial strain is
The required value of Poisson's ratio is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
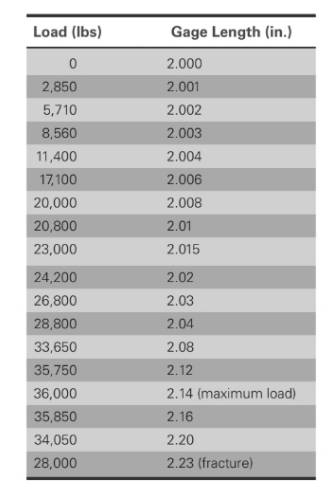
Load for sample is
Diameter of sample is
Based on the given values,
The different values of stress, Strain, gage diameter is shown below:

Calculation of transverse strain,
Where,
Putting the values,
The required value of transverse strain is
Calculation of axial strain,
Where,
Thus, the required value of axial strain is
Calculation of Poisson's ratio,
Putting the value of transverse and axial strain,
Thus, the required value of Poisson's ratio is
(k)
Interpretation:
The value of tensile strength for 416 stainless steel is to be determined. Also, the comparison of values for tensile strength should be explained.
Concept introduction:
Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
Tensile strength is the maximum load that material can withstand without rapture. The above graph is reflecting relationship between stress and strain.
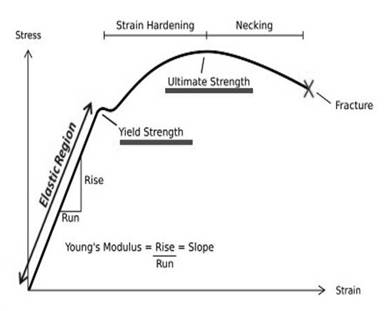
Answer to Problem 6.36P
Thus, the required calculated value of tensile strength is
Thus, the value of tensile strength remains the same after quenching and tempering.
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
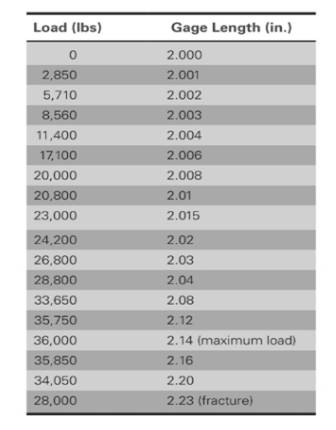
Load for sample is
Diameter of sample is
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
Calculation of stress and strain values are done using spreadsheet shown below,
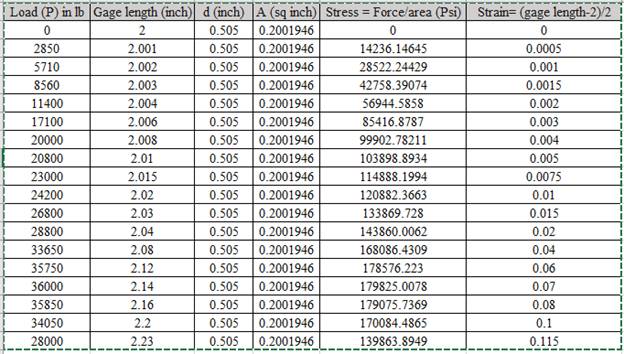
Using the data for Stress-Strain, Drawing the Stress Strain curve,
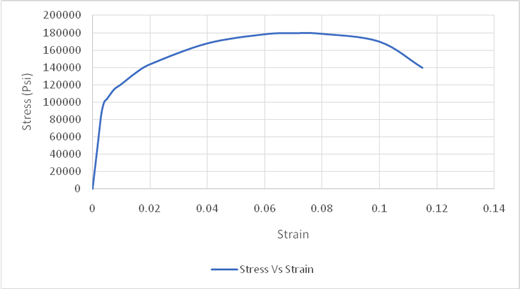
The maximum value of stress is used for obtaining the value of tensile strength. Drawing tie lines as shown in the figure below,
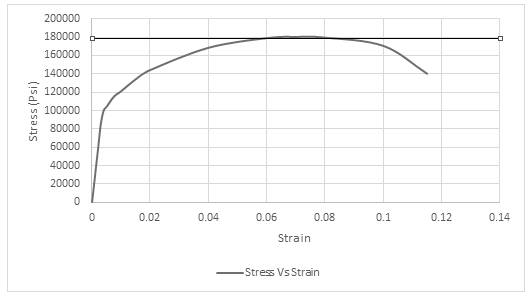
Thus, the required value of tensile strength is
Based on the given information the physical and mechanical properties of 416 stainless steel is shown below:
Thus, the required calculated value of tensile strength is
Thus, the required calculated value of yield strength is
The values of 416 stainless steel when quenched and tempered is shown in table,
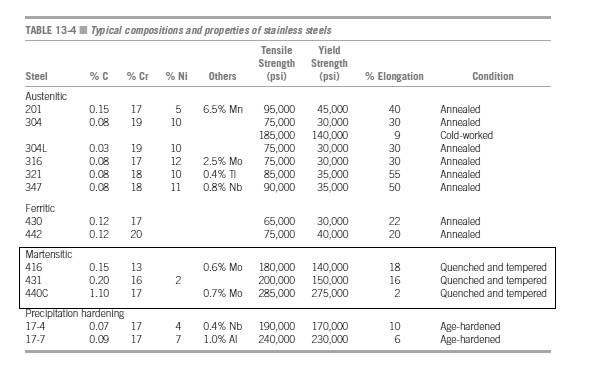
Thus, the value of tensile strength remains the same after quenching and tempering.
Want to see more full solutions like this?
Chapter 6 Solutions
Essentials of Materials Science and Engineering, SI Edition
- What happens to the rotor speed and rotor current when the mechanical load on an in- duction motor increases? Would you recommend using a 50 hp in- duction motor to drive a 10 hp load? Explain. Give two advantages of a wound-rotor mo- tor over a squirrel-cage motor. Both the voltage and frequency induced in the rotor of an induction motor decrease as the rotor speeds up. Explain.arrow_forwardWhat would the electropneumatic diagram of a circuit with the sequence a+b+c+(a-b-c-) look like?arrow_forward### What would the electropneumatic diagram of a circuit with the sequence a+b+c+(a-b-c-) look like, with a counter, in the fluidsim?arrow_forward
- You are asked to design a unit to condense ammonia. The required condensation rate is 0.09kg/s. Saturated ammonia at 30 o C is passed over a vertical plate (10 cm high and 25 cm wide).The properties of ammonia at the saturation temperature of 30°C are hfg = 1144 ́10^3 J/kg andrv = 9.055 kg/m 3 . Use the properties of liquid ammonia at the film temperature of 20°C (Ts =10 o C):Pr = 1.463 rho_l= 610.2 kf/m^3 liquid viscosity= 1.519*10^-4 kg/ ms kinematic viscosity= 2.489*10^-7 m^2/s Cpl= 4745 J/kg C kl=0.4927 W/m CCalculate the surface temperature required to achieve the desired condensation rate of 0.09 kg/s( should be 688 degrees C) a) Show that if you use a bigger vertical plate (2.5 m-wide and 0.8 m-height), the requiredsurface temperature would be now 20 o C. You may use all the properties given as an initialguess. No need to iterate to correct for Tf. b) What if you still want to use small plates because of the space constrains? One way to getaround this problem is to use small…arrow_forwardBorrow pit soil is being used to fill an 900,00 yd3 of depression. The properties of borrowpit and in-place fill soils obtained from laboratory test results are as follows:• Borrow pit soil: bulk density 105 pcf, moisture content = 8%, and specific gravity = 2.65• In-place fill soil: dry unit weight =120 pcf, and moisture content = 16%(a) How many yd3 of borrow soil is required?(b) What water mass is needed to achieve 16% moisture in the fill soil?(c) What is the in-place density after a long rain?arrow_forwardHomework#5arrow_forwardchemical engineering Only solve the specific enthalpies. Be thorough to the fullest for each calculationarrow_forwardQuestion 1: Beam Analysis Two beams (ABC and CD) are connected using a pin immediately to the left of Point C. The pin acts as a moment release, i.e. no moments are transferred through this pinned connection. Shear forces can be transferred through the pinned connection. Beam ABC has a pinned support at point A and a roller support at Point C. Beam CD has a roller support at Point D. A concentrated load, P, is applied to the mid span of beam CD, and acts at an angle as shown below. Two concentrated moments, MB and Mc act in the directions shown at Point B and Point C respectively. The magnitude of these moments is PL. Moment Release A B с ° MB = PL Mc= = PL -L/2- -L/2- → P D Figure 1: Two beam arrangement for question 1. To analyse this structure, you will: a) Construct the free body diagrams for the structure shown above. When constructing your FBD's you must make section cuts at point B and C. You can represent the structure as three separate beams. Following this, construct the…arrow_forward: The Multithreaded Cook In this lab, we'll practice multithreading. Using Semaphores for synchronization, implement a multithreaded cook that performs the following recipe, with each task being contained in a single Thread: 1. Task 1: Cut onions. a. Waits for none. b. Signals Task 4 2. Task 2: Mince meat. a. Waits for none b. Signals Task 4 3. Task 3: Slice aubergines. a. Waits for none b. Signals Task 6 4. Task 4: Make sauce. a. Waits for Task 1, and 2 b. Signals Task 6 5. Task 5: Finished Bechamel. a. Waits for none b. Signals Task 7 6. Task 6: Layout the layers. a. Waits for Task 3, and 4 b. Signals Task 7 7. Task 7: Put Bechamel and Cheese. a. Waits for Task 5, and 6 b. Signals Task 9 8. Task 8: Turn on oven. a. Waits for none b. Signals Task 9 9. Task 9: Cook. a. Waits for Task 7, and 8 b. Signals none At the start of each task (once all Semaphores have been acquired), print out a string of the task you are starting, sleep for 2-11 seconds, then print out a string saying that you…arrow_forwardA differential element on the bracket is subjected to plane strain that has the following components:, Ɛx = 300 × 10-6, Ɛy = 150 × 10-6, Ɛxy = -750 x 10-6. Use the strain-transformation equations and determine the normal strain Ɛx in the X/ direction on an element oriented at an angle of 0 = 40°. Note, a positive angle, 0, is counter clockwise. x Enter your answer in micro strain to a precision of two decimal places. eg. if your answer is 300.15X106, please enter 300.15.arrow_forwardIf the 50 mm diameter shaft is made from brittle material having an ultimate strength of σult=595 MPa for both tension and compression, determine the factor of safety of the shaft against rupture. The applied force, F, is 140 kN. The applied torque T, is 5.0 kN⚫m. Enter your answer to a precision of two decimal places. T Farrow_forwardProgramming Problems 9.28 Assume that a system has a 32-bit virtual address with a 4-KB page size. Write a C program that is passed a virtual address (in decimal) on the command line and have it output the page number and offset for the given address. As an example, your program would run as follows: ./addresses 19986 Your program would output: The address 19986 contains: page number = 4 offset = 3602 Writing this program will require using the appropriate data type to store 32 bits. We encourage you to use unsigned data types as well. Programming Projects Contiguous Memory Allocation In Section 9.2, we presented different algorithms for contiguous memory allo- cation. This project will involve managing a contiguous region of memory of size MAX where addresses may range from 0 ... MAX - 1. Your program must respond to four different requests: 1. Request for a contiguous block of memory 2. Release of a contiguous block of memory 3. Compact unused holes of memory into one single block 4.…arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage,
Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage, Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning
Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION
Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON
Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY
Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY





