Chapter 6, Problem 6.2.14P

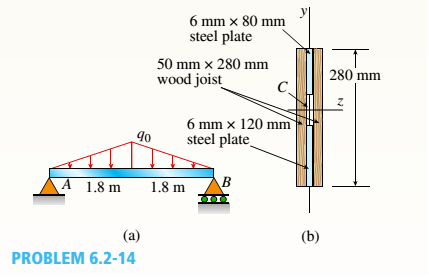
-14 A simply supported composite beam with a 3.6 m span supports a triangularly distributed load of peak intensity q₀at mid-span (see figure part a). The beam is constructed of two wood joists, each 50 mm x 280 mm, fastened to two steel plates, one of dimensions 6 mm × 80 mm and the lower plate of dimensions 6 mm x 120mm (see figure part b). The modulus of elasticity for the wood is 11 GPa and for the steel is 210 GPa.

If the allowable stresses are 7 MPa for the wood and 120 MPa for the steel, find the allowable peak load intensity q_0maxwhen the beam is bent about the z axis. Neglect the weight of the beam.

  

To determine

The peak maximum load intensity $q_{0,\max }$ with the bent beam at the z axis.

Answer to Problem 6.2.14P

The peak maximum load intensity $q_0\approx 15.6kN/m$

Explanation of Solution

Given Information:

The given figure,

  

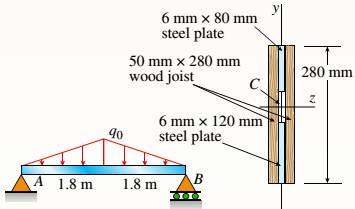
A supported beam with the span of 3.6m supports a load that is triangularly distributed with the peak intensity at the mid span. The two wood joists of the beam each measuring 50mm*280mm that is fastened to steel plates of two that has dimensions of 6mm*80mm and 6mm*120mm. The wood elasticity modulus is 11GPa and for steel it is 210GPa.

By the given equation the neutral axis location is determined,

  $\begin{array}{l}{E}_s{\displaystyle \underset{x}{\int }ydA}+E_w{\displaystyle \underset{w}{\int }ydA}=0\\ E_s(\overline{y_{s1}}{A}_{s1})+E_s(\overline{y_{s2}}{A}_{s2})+E_w(\overline{y_{w3}}{A}_{w3})+E_w(\overline{y_{w4}}{A}_{w4})=0\\ E_s[(\overline{y_{s1}}{A}_{s1})+(\overline{y_{s2}}{A}_{s2})]+E_w(\overline{y_{w3}}{A}_{w3})+E_w(\overline{y_{w4}}{A}_{w4})=0\to (1)\end{array}$

Where,

  $\begin{array}{l}{E}_s-Steelelasticitymodulus\\ E_w-woodelasticitymodulus\end{array}$

Using the figure we have,

The distance between the section 1centroid and composite section neutral axis is,

  $\overline{y_{s1}}=(h_1-40)$

The distance between the section 2 centroid and composite section neutral axis is,

  $\overline{y_{s2}}=(280-h_1-60)$

The distance between the section 3 centroid and composite section neutral axis is,

  $\overline{y_{w3}}=\left(h_1-\frac{280}{2}\right)$

The distance between the section 4 centroid and composite section neutral axis is,

  $\overline{y_{w4}}=\left(h_1-\frac{280}{2}\right)$

Section 1 area $A_{s1}=80*6=480m{m}^2$

Section 2 area $A_{s2}=120*6=720m{m}^2$

Section 3 area $A_{w3}=280*50=14000m{m}^2$

Section 4 area $A_{w4}=280*50=14000m{m}^2$

Substituting the given values in (1)

  $\begin{array}{l}{E}_s[(\overline{y_{s1}}{A}_{s1})+(\overline{y_{s2}}{A}_{s2})]+E_w(\overline{y_{w3}}{A}_{w3})+E_w(\overline{y_{w4}}{A}_{w4})=0\\ 210*\left|{10}^3\right|[(h_1-40)480+[-(280-h_1-60)]720]+11*\left|{10}^3\right|[(h_1-40)14000+[h_1-140]14000]=0\end{array}$

  $h_1=143.6mm$

Assume the load is symmetric at the span centre. So at point A the reaction is half the total load

  $R_A=\frac{1}{2}*1.8*q_0$

  $=0.9q_0$

The bending moment maximum is seen at the mid span as the symmetric load is at the span centre.

In the diagram the beam at the mid span is cut and the equilibrium cut at the left side is considered. Here M is considered as the bending moment maximum.

The right section moment is given as,

  $\begin{array}{l}{\displaystyle \sum M_{mid}}=0\\ -R_A*1.8+\frac{1}{2}*1.8*q_0\left(\frac{1}{3}*1.8\right)+M=0\\ -0.9q_0*1.8+\frac{1}{2}*1.8*q_0\left(\frac{1}{3}*1.8\right)+M=0\\ -0.9q_0*2.3*1.8*q_0\left(0.6\right)+M=0\\ M=1.08q_{0}Nm\end{array}$

  $=1.08q_{0}Nm*\left|\frac{{10}^{3}mm}{1m}\right|\Rightarrow 1080q_{0}Nmm$

With the help of parallel axis theorem the steel section’s second moment of inertia at the neutral axis is determined.

  $I_s=I_{s1}+I_{s2}$

  $\begin{array}{l}=\left(\frac{b_1{d}_1^3}{12}+A_{s1}{\left(\overline{y_{s1}}\right)}^2\right)+\left(\frac{b_2{d}_2^3}{12}+A_{s2}{\left(\overline{y_{s2}}\right)}^2\right)\\ =\left(\frac{6*{80}^3}{12}+(6*80){\left(h_1-40\right)}^2\right)+\left(\frac{6*{120}^3}{12}+(6*120){\left(280-h_1-60\right)}^2\right)\end{array}$

  $\begin{array}{l}=\left(\frac{6*{80}^3}{12}+(6*80){\left(143.6-40\right)}^2\right)+\left(\frac{6*{120}^3}{12}+(6*120){\left(280-143.6-60\right)}^2\right)\\ =\left(3072000+(480){\left(103.6\right)}^2\right)+\left(864000+(720){\left(280-143.6-60\right)}^2\right)\\ =10474432m{m}^4\end{array}$

With the help of parallel axis theorem the wooden section’s second moment of inertia at the neutral axis is determined.

  $I_w=I_{w3}+I_{w4}$

  $\begin{array}{l}=\left(\frac{b_3{d}_3^3}{12}+A_{w3}{\left(\overline{y_{w3}}\right)}^2\right)+\left(\frac{b_4{d}_4^3}{12}+A_{w4}{\left(\overline{y_{s4}}\right)}^2\right)\\ =\left(\frac{50*{280}^3}{12}+(50*2800){\left(h_1-\frac{280}{2}\right)}^2\right)+\left(\frac{50*{280}^3}{12}+(5*2800){\left(h_1-\frac{280}{2}\right)}^2\right)\end{array}$

  $\begin{array}{l}=\left(\frac{50*{280}^3}{12}+(50*2800){\left(143.6-\frac{280}{2}\right)}^2\right)+\left(\frac{50*{280}^3}{12}+(5*2800){\left(143.6-\frac{280}{2}\right)}^2\right)\\ =186562133m{m}^4\end{array}$

The equation of the flexural stress at the maximum of the steel that has the top layer,

  ${\sigma }_{ts}=-\frac{M{h}_1{E}_s}{E_s{I}_s+E_w{I}_w}$

Substituting the values we have,

  $-120=-\frac{1080q_0*143.6*210*\left|{10}^3\right|}{210*\left|{10}^3\right|*10474432+11*\left|{10}^3\right|*186562133}\to (2)$

  $q_0=15666N/m$

As the top layer of the steel is compressive the negative sign is given in the equation (2)

The equation of the flexural stress at the maximum of the steel that has the bottom layer,

  ${\sigma }_{bs}=-\frac{M\left(-h_2\right)E_s}{E_s{I}_s+E_w{I}_w}$

  $\begin{array}{l}120=-\frac{1080q_0{E}_s}{E_s{I}_s+E_w{I}_w}\\ -120=-\frac{1080q_0*\left(-(280-143.6)\right)*210*\left|{10}^3\right|}{210*\left|{10}^3\right|*10474432+11*\left|{10}^3\right|*186562133}\to (3)\end{array}$

  $q_0=16493N/m$

The equation of the flexural stress at the maximum of the wood that has the top layer,

  ${\sigma }_{tw}=-\frac{M\left(h_1\right)E_w}{E_s{I}_s+E_w{I}_w}$

  $-7=-\frac{1080q_0*143.6*11*\left|{10}^3\right|}{210*\left|{10}^3\right|*10474432+11*\left|{10}^3\right|*186562133}\to (4)$

  $q_0=17446N/m$

The equation of the flexural stress at the maximum of the wood that has the bottom layer,

  ${\sigma }_{bw}=-\frac{M\left(-(280-h_1)\right)E_w}{E_s{I}_s+E_w{I}_w}$

  $7=-\frac{1080q_0*\left(-(280-143.6)\right)*11*\left|{10}^3\right|}{210*\left|{10}^3\right|*10474432+11*\left|{10}^3\right|*186562133}\to (5)$

  $q_0=18367N/m$

The load with the lowest magnitude is selected from the equations (2), (3), (4), (5)

  $q_0=15666N/m\approx 15.6kN/m$

Conclusion:

Thus, the peak maximum load intensity is calculated by substituting section areas in equation 1.