
Concept explainers
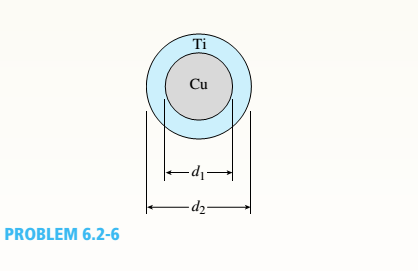
A r o lukI f/frm f «m t ub e of ou t sid e d ia met er ^ and a copper core of diameter dxare bonded to form a composite beam, as shown in the figure,
(a) Derive formulas for the allowable bending moment M that can be carried by the beam based upon an allowable stress <7Ti in the titanium and an allowable stress
copper (Assume that the moduli of elasticity for the titanium and copper are Er- and £Cu, respectively.)
(b)
If d1= 40 mm, d{= 36 mm, ETl= 120 GPa, ECu= 110 GPa, o-Ti = 840 MPa, and
ctqj = 700 MPa, what is the maximum bending moment Ml (c)
What new value of copper diameter dtwill result
in a balanced design? (i.e., a balanced design is
that in which titanium and copper reach allow-
able stress values at the same time).
i.
The formula for the allowable bending moment M for titanium tube and copper core of the composite beam
Answer to Problem 6.2.6P
Explanation of Solution
Given:
Allowable stress for titanium is sti
Allowable stress for titanium is scu
Diameter of the copper rod = d1
Outer Diameter of the titanium rod = d2
Concept Used:
Calculation:
Conclusion:
ii.
The allowable bending moment for titanium and copper.
Answer to Problem 6.2.6P
Allowable bending moment for titanium, Mallowableti = 4989 N-m
Allowable bending moment for Copper, MallowableCu =5039.6 N-m
Explanation of Solution
Given:
Allowable stress for titanium, sti = 840 MPa
Allowable stress for titanium, scu= 700 MPa
Diameter of the copper rod, d1= 36 mm
Outer Diameter of the titanium rod, d2 = 40 mm
Eti= 110 GPa
Ecu= 120 GPa
Concept Used:
Calculation:
Allowable bending moment for titanium, Mallowableti = 4989 N-m
Allowable bending moment for Copper, MallowableCu =5039.6 N-m
iii.
The value of the diameter of the copper rod for a balanced design
Answer to Problem 6.2.6P
The diameter of the copper for a balanced design is 36.4 mm
Explanation of Solution
Given:
Allowable stress for titanium, sti = 840 MPa
Allowable stress for titanium, scu= 700 MPa
Outer Diameter of the titanium rod, d2 = 40 mm
Eti= 110 GPa
Ecu= 120 GPa
Concept Used:
Calculation:
Conclusion:
The diameter of the copper for a balanced design is 36.4 mm
Want to see more full solutions like this?
Chapter 6 Solutions
Mechanics of Materials (MindTap Course List)
- Two large tanks, each holding 100 L of liquid, are interconnected by pipes, with the liquid flowing from tank A into tank B at a rate of 3 L/min and from B into A at a rate of 1 L/min (see Figure Q1). The liquid inside each tank is kept well stirred. A brine solution with a concentration of 0.2 kg/L of salt flows into tank A at a rate of 6 L/min. The diluted solution flows out of the system from tank A at 4 L/min and from tank B at 2 L/min. If, initially, tank A contains pure water and tank B contains 20 kg of salt. A 6 L/min 0.2 kg/L x(t) 100 L 4 L/min x(0) = 0 kg 3 L/min B y(t) 100 L y(0) = 20 kg 2 L/min 1 L/min Figure Q1 - Mixing problem for interconnected tanks Determine the mass of salt in each tank at time t > 0: Analytically (hand calculations)arrow_forwardplease help solvearrow_forwardplease help solvearrow_forward
- please help solvearrow_forwardplease help solvearrow_forwardA steam pipe is covered with two layers of insulation. The inner layer (k = 0.17 W/m-K) is 30 mm thick and outer layer (k = 0.023 W/m-K) is 50 mm thick. The pipe is made of steel (k = 58 W/m-K) and has inner diameter and outer diameter of 160 and 170 mm, respectively. The temperature of saturated steam is 300 °C and the ambient air is at 50 °C. If the inside and outside heat transfer coefficients are 30 W/m²K and 5.8 W/m²-K respectively, calculate the rate of heat loss per unit length of the pipe.arrow_forward
- An aluminium pipe carries steam at 110 °C. The pipe (k 185 W/m °C) has an inner diameter of 100 mm and an outer diameter of 120 mm. the pipe is located in a room where the ambient air temperature is 30 °C and the convective heat transfer coefficient between the pipe and air is 15 W/m2°C. .2.1) Neglecting the convective resistance of the steam, determine the heat transfer rate per unit length of pipe. hs o 1101 2.2) To reduce the heat loss from the pipe, it is covered with a 50 mm thick layer of insulation (k 0.20 W/m C). Determine the heat transfer rate per unit length from the insulated pipe. Assume negligible convective resistance from the steamarrow_forward問題1 Facilities planning activities include... product design facility layout design process design all of the abovearrow_forward16.1. The cart has mass M and is filled with water that has a mass mo. If a pump ejects water through a nozzle having a cross-sectional area A at a constant rate of vo relative to the cart, determine the velocity of the cart as a function of time. What is the maximum speed developed by the cart assuming all the water can be pumped out? Assume the frictional resistance to forward motion is F and the density of water is p.arrow_forward
- 16.2 A block of mass 10 kg is subjected to a force F(t) at an angle 30° from the horizontal that is at a constant 12 N for 3 seconds and is suddenly increased to 18 N afterwards. A constant 1 N force acts on the block as shown as well. The static and kinetic friction coefficients between the block and the ground is 0.15 and 0.10, respectively. Determine the magnitude and direction of the velocity of the block after 5 seconds. Ms=0.15 Mk = 0.10 F(t) [N] F(t) 18 1 N 30° m = 10 kg 12 t [s] 3arrow_forwardNo chatgptarrow_forwardplease help me solve this equationarrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
