Chapter 6, Problem 6.2.15P

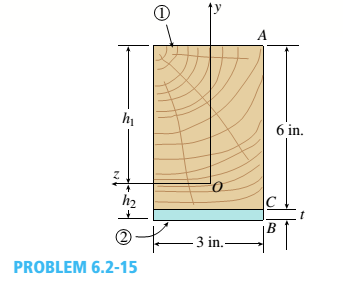
-15 A composite beam is constructed froma wood beam (3 in. x 6 in.) and a steel plate (3 in, wide). The wood and the steel are securely fastened to act as a single beam. The beam is subjected to a positive bending moment M. = 75 kip-in. Calculate the required thickness of the steel plate based on the following limit states:

1. Allowable compressive stress in the wood = 2 ksi
2. Allowable tensile stress in the wood = 2 ksi
3. Allowable tensile stress in the steel plate = 16 ksi
Assume that E_w= 1,500 ksi and e_s= 30,000 ksi.

  

To determine

The thickness required for the steel plate.

Answer to Problem 6.2.15P

The thickness required for the steel plate $t_s=0.356in.$

Explanation of Solution

Given:

The given figure $$

  

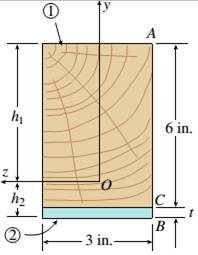
The wooden beam of 3in.*6in. and steel plate with wide 3in. forms the beam. The positive bending moment is given as $M_z=75kip.in$ . Compressive stress that is maximum is 2 ksi.

Concept Used: $$

Normal stress that is maximum for steel,

  ${\sigma }_{sa}=\frac{M_2{h}_2\left(E_s\right)}{E_s{I}_s+E_w{I}_w}$

Where,

  $\begin{array}{l}{M}_2=bendingmoment\\ I_w=woodInertiamoment\\ I_s=steelInertiamoment\\ E_W=wood\mathrm{mod}ulusElasticity\\ E_s=Steel\mathrm{mod}ulusElasticity\\ h_2=height\end{array}$

Calculation:

Neutral axis location at the lower end is given as,

  $h_2=\frac{E_s(b{t}_s)\frac{t_s}{2}+E_w(b{h}_w)\left(t_s+\frac{h_w}{2}\right)}{E_s(b{t}_s)+E_w(b{h}_w)}$

Substituting the values we have,

  $=\frac{30000t_s{}^2+1500(6)\left(2t_s+6\right)}{2(30000t_s)+1500(6)}$

  $\begin{array}{l}=\frac{10t_s{}^2+6t_s+18}{20t_s+6}\\ =\frac{5t_s{}^2+3t_s+9}{10t_s+3}\end{array}$

From the top the neutral axis distance is given as,

  $h_1=h_w+t_s-h_2$

  $\begin{array}{l}=6+t_s-\frac{5t_s^2+3t_s+9}{10t_s+3}\\ =\frac{\left(6+t_s\right)\left(3+10t_s\right)-\left(5t_s^2+3t_s+9\right)}{10t_s+3}\Rightarrow \frac{\left(60t_s\right)+10t_s+3t_s+18-5t_s^2-3t_s-9}{10t_s+3}\\ =\frac{\left(60t_s\right)+5t_s^2+9}{10t_s+3}\end{array}$

The wooden section moment of inertia is given as,

  $I_w=\frac{b{h}_{{}^w}^3}{12}+b{h}_w{\left(h_1-\frac{h_w}{2}\right)}^2$

  $\begin{array}{l}=\frac{3*6_{}^3}{12}+3*6{\left(\frac{\left(60t_s\right)+5t_s^2+9}{10t_s+3}-\frac{6}{2}\right)}^2\\ =\frac{648}{12}+18{\left(\frac{\left(60t_s\right)+5t_s^2+9}{10t_s+3}-\frac{6}{2}\right)}^2\\ =54+18{\left(\frac{5t_s^2+30t_s}{10t_s+3}\right)}^2\end{array}$

The steel section moment of inertia is given as,

  $I_s=\frac{b{t}_{{}^s}^3}{12}+b{t}_s{\left(h_2-\frac{t_s}{2}\right)}^2$

  $\begin{array}{l}=\frac{3t_{{}^s}^3}{12}+3t_s{\left(\frac{5t_s{}^2+3t_s+9}{10t_s+3}-\frac{t_s}{2}\right)}^2\\ =\frac{t_{{}^s}^3}{4}+3t_s{\left(\frac{10t_s{}^2+6t_s+18-10t_s{}^2-3t_s}{20t_s+6}\right)}^2\\ =\frac{t_{{}^s}^3}{4}+3t_s{\left(\frac{3t_s+18}{20t_s+6}\right)}^2\end{array}$

The normal stress that is maximum in the section of steel,

  ${\sigma }_{sa}=\frac{M_2{h}_2\left(E_s\right)}{E_s{I}_s+E_w{I}_w}$

  $16=\frac{75\left(\frac{5t_s{}^2+3t_s+9}{10t_s+3}\right)\left(30000\right)}{30000\left(\frac{t_s^3}{4}+3t_s{\left(\frac{3t_s+18}{20t_s+6}\right)}^2\right)+1500\left(54+18{\left(\frac{5t_s{}^2+30t_s}{10t_s+3}\right)}^2\right)}$

  $16=\frac{225\left(\frac{5t_s{}^2+3t_s+9}{10t_s+3}\right)\left(30000\right)}{0.375\left(\frac{t_s{}^3{(20t_s+6)}^2+12t_s{(3t_s+18)}^2}{{\left(10t_s+3\right)}^2}\right)+0.15\left(\frac{54{(10t_s+3)}^2+18{\left(5t_s{}^2+30t_s\right)}^2}{{\left(10t_s+3\right)}^2}\right)}$

  $t_s=0.356in.$

Conclusion:

Thus, the thickness required for the steel plate is calculated by equating bending movement, wood inertia, steel inertia, steel inertia, wood modulus elasticity, steel modulus elasticity and height.

To determine

The thickness required for the steel plate.

Answer to Problem 6.2.15P

The thickness required for the steel plate $t_s=0.755in.$

Explanation of Solution

Given:

The given figure:

  

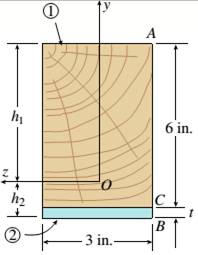
The wooden beam of 3in.*6in. and steel plate with wide 3in. forms the beam. The positive bending moment is given as $M_z=75kip.in$ . Tensile stress that is maximum in the wood is 2 ksi.

Concept Used:

Wood maximum stress of top part is given as,

  ${\sigma }_{wa}=\frac{M_2{h}_1\left(E_w\right)}{E_s{I}_s+E_w{I}_w}$

Where,

  $\begin{array}{l}M=Maximumstress\\ I_s=steelInertiamoment\\ I_w=woodInertiamoment\\ E_W=wood\mathrm{mod}ulusElasticity\\ E_s=steel\mathrm{mod}ulusElasticity\\ h_1=height\end{array}$

Calculation:

Normal Maximum stress for Wood at the top,

  ${\sigma }_{wa}=\frac{M_2{h}_1\left(E_w\right)}{E_s{I}_s+E_w{I}_w}$

Substituting the values we have,

  $2=\frac{75\left(\frac{5t_s{}^2+60t_s+9}{10t_s+3}\right)\left(1500\right)}{30000\left(\frac{t_s^3}{4}+3t_s{\left(\frac{3t_s+18}{20t_s+6}\right)}^2\right)+1500\left(54+18{\left(\frac{5t_s{}^2+30t_s}{10t_s+3}\right)}^2\right)}$

  $2=\frac{11.25\left(\frac{5t_s{}^2+60t_s+9}{10t_s+3}\right)}{0.375\left(\frac{t_s{}^3{(20t_s+6)}^2+12t_s{(3t_s+18)}^2}{{\left(10t_s+3\right)}^2}\right)+0.15\left(\frac{54{(10t_s+3)}^2+18{\left(5t_s{}^2+30t_s\right)}^2}{{\left(10t_s+3\right)}^2}\right)}$

  $t_s=0.755in.$

Conclusion:

Thus, the thickness required for the steel plate is calculated by wood modulus elasticity, steel modulus elasticity and height.

To determine

The thickness required for the steel plate.

Answer to Problem 6.2.15P

  $t_s=0.079in.$

Explanation of Solution

Given:

The given figure:

  

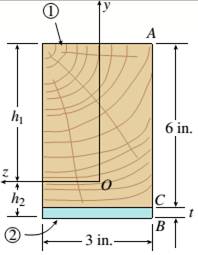
The wooden beam of 3in.*6in. and steel plate with wide 3in. forms the beam. The positive bending moment is given as $M_z=75kip.in$ . Tensile stress that is maximum in the steel is 16 ksi.

Concept Used:

Wood maximum stress of bottom part is given as,,

  ${\sigma }_{wa}=\frac{M_2\left(h_2-t_s\right)\left(E_w\right)}{E_s{I}_s+E_w{I}_w}$

Where,

  $\begin{array}{l}M=Maximumstress\\ I_s=steelInertiamoment\\ I_w=woodInertiamoment\\ E_W=wood\mathrm{mod}ulusElasticity\\ E_s=steel\mathrm{mod}ulusElasticity\\ h_1=height\end{array}$

Calculation:

Maximum stress Maximum for Wood at the bottom,

  ${\sigma }_{pw}=\frac{M_{pw}\left(\frac{h_1}{2}\right)\left(E_{pw}\right)}{E_{pw}{I}_1+E_p{I}_2}$

Substituting the values we have,

  $2=\frac{75\left(\frac{5t_s{}^2+3t_s+9}{10t_s+3}-t_s\right)\left(1500\right)}{30000\left(\frac{t_s^3}{4}+3t_s{\left(\frac{3t_s+18}{20t_s+6}\right)}^2\right)+1500\left(54+18{\left(\frac{5t_s{}^2+30t_s}{10t_s+3}\right)}^2\right)}$

  $2=\frac{11.25\left(\frac{5t_s{}^2+3t_s+9-10t_s^2-3t_s}{10t_s+3}\right)}{0.375\left(\frac{t_s{}^3{(20t_s+6)}^2+12t_s{(3t_s+18)}^2}{{\left(10t_s+3\right)}^2}\right)+0.15\left(\frac{54{(10t_s+3)}^2+18{\left(5t_s{}^2+30t_s\right)}^2}{{\left(10t_s+3\right)}^2}\right)}$

  $t_s=0.079in.$

Conclusion:

Thus, the thickness required for the steel plate is calculated by maximum stress, steel inertia moment, wood inertia moment , wood modulus elasticity, steel modulus elasticity.