
Concept explainers
(a) Find a linear function that contains the points
(b) Find a quadratic function with the vertex
(c) Show that there is no exponential function of the form
(a)
To calculate: The equation, slope, and intercepts of line containing the points
Answer to Problem 14CR
Solution:
The linear equation passing through points
The slope of the linear function passing through points
The
The
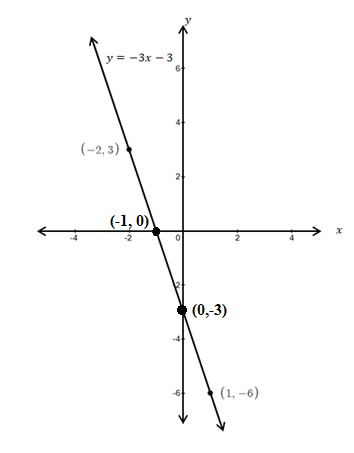
The graph of the linear function is
Explanation of Solution
Given information:
The points
Formula used:
1) Slope formula: The slope between two points
2) Equation of the line using point-slope formula:
The equation of line having slope
Calculation:
Consider
The slope using
Use the point-slope form the equation of the line is
Use the point
Substitute
Thus, the
Substitute
Thus, the
To graph this linear function, follow these steps:
Step 1: Plot the points
Step 2: Sketch a straight line passing through the points

This is the graph of the linear function passing through the points
(b)
The equation and intercepts of the quadratic function with vertex
Answer to Problem 14CR
Solution:
The quadratic equation is
The
The
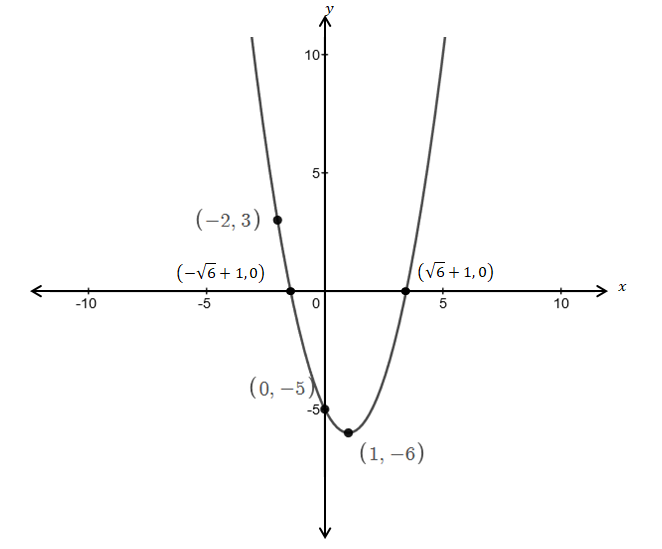
The graph of the quadratic function is
Explanation of Solution
Given information:
The vertex is at
Explanation:
Vertex form of the quadratic equation with vertex at
Vertex is at
Substitute
Consider
Solve for
From
Substitute
Solve for
Thus, the
Substitute
Thus, the
To graph this quadratic function, follow these steps:
Step 1: Plot the vertex
Step 2: Plot the point
Step 2: Sketch a smooth curve passing through all points and the shape is like parabola.

This is the graph of the quadratic function with the vertex is at
(c)
To show: There is no exponential function of the form
Explanation of Solution
Given information:
The points are
Formula used:
If
Proof:
Replace
Using, “If
Consider
Solve for
Consider
Solve for
For point
Hence, proved
Chapter 6 Solutions
Precalculus
Additional Math Textbook Solutions
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Elementary Statistics
College Algebra (7th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Introductory Statistics
Pre-Algebra Student Edition
- nd ave a ction and ave an 48. The domain of f y=f'(x) x 1 2 (= x<0 x<0 = f(x) possible. Group Activity In Exercises 49 and 50, do the following. (a) Find the absolute extrema of f and where they occur. (b) Find any points of inflection. (c) Sketch a possible graph of f. 49. f is continuous on [0,3] and satisfies the following. X 0 1 2 3 f 0 2 0 -2 f' 3 0 does not exist -3 f" 0 -1 does not exist 0 ve tes where X 0 < x <1 1< x <2 2arrow_forwardNumerically estimate the value of limx→2+x3−83x−9, rounded correctly to one decimal place. In the provided table below, you must enter your answers rounded exactly to the correct number of decimals, based on the Numerical Conventions for MATH1044 (see lecture notes 1.3 Actions page 3). If there are more rows provided in the table than you need, enter NA for those output values in the table that should not be used. x→2+ x3−83x−9 2.1 2.01 2.001 2.0001 2.00001 2.000001arrow_forwardFind the general solution of the given differential equation. (1+x)dy/dx - xy = x +x2arrow_forwardEstimate the instantaneous rate of change of the function f(x) = 2x² - 3x − 4 at x = -2 using the average rate of change over successively smaller intervals.arrow_forwardGiven the graph of f(x) below. Determine the average rate of change of f(x) from x = 1 to x = 6. Give your answer as a simplified fraction if necessary. For example, if you found that msec = 1, you would enter 1. 3' −2] 3 -5 -6 2 3 4 5 6 7 Ꮖarrow_forwardGiven the graph of f(x) below. Determine the average rate of change of f(x) from x = -2 to x = 2. Give your answer as a simplified fraction if necessary. For example, if you found that msec = , you would enter 3 2 2 3 X 23arrow_forwardA function is defined on the interval (-π/2,π/2) by this multipart rule: if -π/2 < x < 0 f(x) = a if x=0 31-tan x +31-cot x if 0 < x < π/2 Here, a and b are constants. Find a and b so that the function f(x) is continuous at x=0. a= b= 3arrow_forwardUse the definition of continuity and the properties of limits to show that the function is continuous at the given number a. f(x) = (x + 4x4) 5, a = -1 lim f(x) X--1 = lim x+4x X--1 lim X-1 4 x+4x 5 ))" 5 )) by the power law by the sum law lim (x) + lim X--1 4 4x X-1 -(0,00+( Find f(-1). f(-1)=243 lim (x) + -1 +4 35 4 ([ ) lim (x4) 5 x-1 Thus, by the definition of continuity, f is continuous at a = -1. by the multiple constant law by the direct substitution propertyarrow_forward1. Compute Lo F⚫dr, where and C is defined by F(x, y) = (x² + y)i + (y − x)j r(t) = (12t)i + (1 − 4t + 4t²)j from the point (1, 1) to the origin.arrow_forward2. Consider the vector force: F(x, y, z) = 2xye²i + (x²e² + y)j + (x²ye² — z)k. (A) [80%] Show that F satisfies the conditions for a conservative vector field, and find a potential function (x, y, z) for F. Remark: To find o, you must use the method explained in the lecture. (B) [20%] Use the Fundamental Theorem for Line Integrals to compute the work done by F on an object moves along any path from (0,1,2) to (2, 1, -8).arrow_forwardhelp pleasearrow_forwardIn each of Problems 1 through 4, draw a direction field for the given differential equation. Based on the direction field, determine the behavior of y as t → ∞. If this behavior depends on the initial value of y at t = 0, describe the dependency.1. y′ = 3 − 2yarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





