
Carrying a Ladder around a Corner Two hallways, one of width 3 feet, the other of width 4 feet, meet at a right angle. See the illustration.
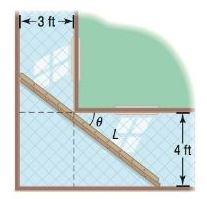
(a) Show that the length of the ladder shown as a function of the angle is
(b) Graph
(c) For what value of is the least?
(d) What is the length of the longest ladder that can be carried around the corner? Why is this also the least value of ?
To find:
a. show that the length
Answer to Problem 51AYU
Solution:
a.
Explanation of Solution
Given:
The function
Calculation:
a. To solve this we divide up the length
To find:
b. Graph
Answer to Problem 51AYU
Solution:
b. graph.
Explanation of Solution
Given:
The function
Calculation:
b. Noting how the interval provided is an open interval(due to the undefined nature of the terms at those end points) we must in reality graph the function along a close but smaller interval, say
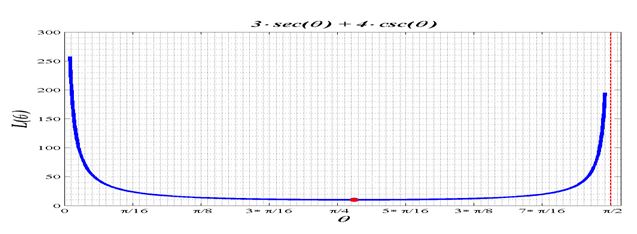
To find:
c. For what value of
Answer to Problem 51AYU
Solution:
c.
Explanation of Solution
Given:
The function
Calculation:
c. From the above figure we can see a symmetric like bowl shape made by the curve for this interval. Being symmetric the curve decreases from the left and increases to the right, which appears to have a minimum right at the center of the interval
To find:
d. What is the length of the longest ladder that can be carried around the corner? Why is this also the least value of
Answer to Problem 51AYU
Solution:
d.
Explanation of Solution
Given:
The function
Calculation:
d. Since the above equation uses the full ladder possible for each value
It is that point where the ladder can perfectly fit and be the longest it can be to be carried around the corner. In calculus class we can show that the angle theta that permits this is:
And the corresponding ladder length is
Chapter 6 Solutions
Precalculus
Additional Math Textbook Solutions
Elementary Statistics (13th Edition)
A First Course in Probability (10th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Elementary Statistics
Thinking Mathematically (6th Edition)
Calculus: Early Transcendentals (2nd Edition)
- "P3 Question 3: Construct the accessibility matrix Passociated with the following graphs, and compute P2 and identify each at the various two-step paths in the graph Ps P₁ P₂arrow_forwardA cable television company estimates that with x thousand subscribers, its monthly revenue and cost (in thousands of dollars) are given by the following equations. R(x) = 45x - 0.24x2 C(x) = 257 + 13xarrow_forwardx³-343 If k(x) = x-7 complete the table and use the results to find lim k(x). X-7 x 6.9 6.99 6.999 7.001 7.01 7.1 k(x) Complete the table. X 6.9 6.99 6.999 7.001 7.01 7.1 k(x) (Round to three decimal places as needed.)arrow_forward
- (3) (4 points) Given three vectors a, b, and c, suppose: |bx c = 2 |a|=√√8 • The angle between a and b xc is 0 = 135º. . Calculate the volume a (bxc) of the parallelepiped spanned by the three vectors.arrow_forwardCalculate these limits. If the limit is ∞ or -∞, write infinity or-infinity. If the limit does not exist, write DNE: Hint: Remember the first thing you check when you are looking at a limit of a quotient is the limit value of the denominator. 1. If the denominator does not go to 0, you should be able to right down the answer immediately. 2. If the denominator goes to 0, but the numerator does not, you will have to check the sign (±) of the quotient, from both sides if the limit is not one-sided. 3. If both the numerator and the denominator go to 0, you have to do the algebraic trick of rationalizing. So, group your limits into these three forms and work with them one group at a time. (a) lim t-pi/2 sint-√ sin 2t+14cos ² t 7 2 2 2cos t (b) lim sint + sin 2t+14cos = ∞ t-pi/2 2 2cos t (c) lim cost-√sin 2t+14cos² t = t-pi/2 2cos t (d) lim t→pi/2 cost+√ sin t + 14cos 2cos ² t = ∞ (e) lim sint-v sin 2 t + 14cos = 0 t-pi/2 (f) lim t-pi/2 sin t +√ sin 2sin 2 t 2 t + 14cos t 2sin t cost- (g)…arrow_forwardThink of this sheet of paper as the plane containing the vectors a = (1,1,0) and b = (2,0,0). Sketch the parallelogram P spanned by a and b. Which diagonal of P represents the vector a--b geometrically?arrow_forward
- (1) (14 points) Let a = (-2, 10, -4) and b = (3, 1, 1). (a) (4 points) Using the dot product determine the angle between a and b. (b) (2 points) Determine the cross product vector axb. (c) (4 points) Calculate the area of the parallelogram spanned by a and b. Justify your answer. 1arrow_forward(d) (4 points) Think of this sheet of paper as the plane containing the vectors a = (1,1,0) and b = (2,0,0). Sketch the parallelogram P spanned by a and b. Which diagonal of P represents the vector ab geometrically? d be .dx adjarrow_forward(2) (4 points) Find all vectors v having length 1 that are perpendicular to both =(2,0,2) and j = (0,1,0). Show all work. a=arrow_forward
- For the following function, find the full power series centered at a of convergence. 0 and then give the first 5 nonzero terms of the power series and the open interval = f(2) Σ 8 1(x)--(-1)*(3)* n=0 ₤(x) = + + + ++... The open interval of convergence is: 1 1 3 f(x)= = 28 3x6 +1 (Give your answer in help (intervals) .)arrow_forwardFor the following function, find the full power series centered at x = 0 and then give the first 5 nonzero terms of the power series and the open interval of convergence. f(x) = Σ| n=0 9 f(x) = 6 + 4x f(x)− + + + ++··· The open interval of convergence is: ☐ (Give your answer in help (intervals) .)arrow_forwardLet X be a random variable with the standard normal distribution, i.e.,X has the probability density functionfX(x) = 1/√2π e^-(x^2/2)2 .Consider the random variablesXn = 20(3 + X6) ^1/2n e ^x^2/n+19 , x ∈ R, n ∈ N.Using the dominated convergence theorem, prove that the limit exists and find it limn→∞E(Xn)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





