Chapter 6.6, Problem 29AYU

(a)

To determine

To find: The scatter diagram for the data for one period.

Answer to Problem 29AYU

The scatter plot is shown in Figure 1

Explanation of Solution

Given:

The given data is shown in Table 1

Table 1

Month $x$	Average Monthly Temperature F
1	24.2
2	28.4
3	32.7
4	39.7
5	47.0
6	53.0
7	56.0
8	55.0
9	49.4
10	42.2
11	32.0
12	27.1

Calculation:

The data of the table represents the average monthly temperature over a period of one year. The scatter diagram is drawn by taking months along the x axis and the average monthly temperature along the y axis.

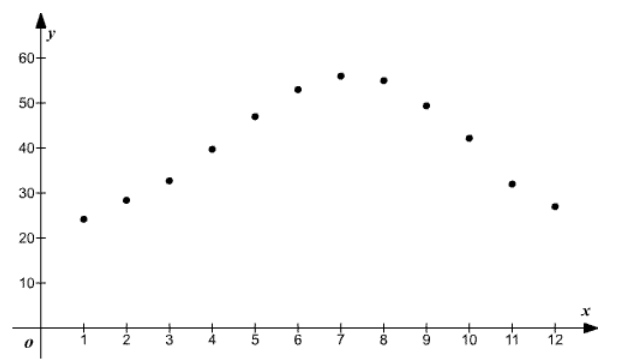
Figure 1

(b)

To determine

To find: The sinusoidal function of the form $y=A\sin \left(\omega x-\varphi \right)+B$ that models the data..

Answer to Problem 29AYU

The sinusoidal model is $y=15.9\sin \left(\frac{\pi }{6}\left(x-4\right)\right)+40.1$ .

Explanation of Solution

Consider the form of the sinusoidal function is,

  $y=A\sin \left(\omega x-\varphi \right)+B$

Consider the amplitude of the sinusoidal function is,

  $\begin{array}{c}A=\frac{56-24.2}{2}\\ =15.9\end{array}$

Consider the value of the vertical shift is,

  $\begin{array}{c}V=\frac{56+24.2}{2}\\ =40.1\end{array}$

Consider the time period of the sinusoidal function is,

  $\begin{array}{l}T=\frac{2\pi }{\omega }\\ 12=\frac{2\pi }{\omega }\\ \omega =\frac{\pi }{6}\end{array}$

The time is divided into four sub intervals as $\left[0,3\right],\left[3,6\right],\left[6,9\right],\left[9,12\right]$ , the time is increasing at the interval $\left(0,3\right)$ and decreasing at the interval $\left(3,9\right)$ .

The local maximum is at $x=3$ .

The local minimum is at $x=7$ .

The required horizontal shift is 4 units to the right.

So, the sinusoidal model is,

  $y=15.9\sin \left(\frac{\pi }{6}\left(x-4\right)\right)+40.1$

(c)

To determine

To find: The scatter diagram for the sinusoidal function found in part (c).

Explanation of Solution

Consider the sinusoidal function is,

  $y=15.9\sin \left(\frac{\pi }{6}\left(x-4\right)\right)+40.1$

The sinusoidal function scatter plot with the help of graphing utility is shown in Figure 2

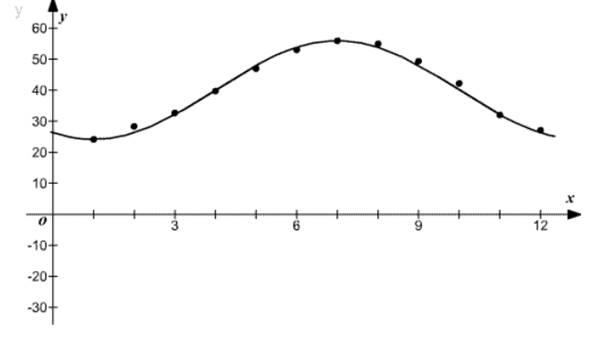
Figure 2

(d)

To determine

To find: The best fit sinusoidal function.

Answer to Problem 29AYU

The expression for the best fit curve is $y=15.619\sin \left(0.517x+4.187\right)+40.377$ .

Explanation of Solution

Consider the sinusoidal function is,

  $y=15.9\sin \left(\frac{\pi }{6}\left(x-4\right)\right)+40.1$

Consider the best fit curve with the help of graphing utility is,

  $y=15.619\sin \left(0.517x+4.187\right)+40.377$

(e)

To determine

To find: The plot of sinusoidal function of best fit.

Answer to Problem 29AYU

The plot is shown in Figure 3

Explanation of Solution

Consider the best fit function is,

  $y=15.619\sin \left(0.517x+4.187\right)+40.377$

The scatter plot for the best fit function is shown in Figure 3

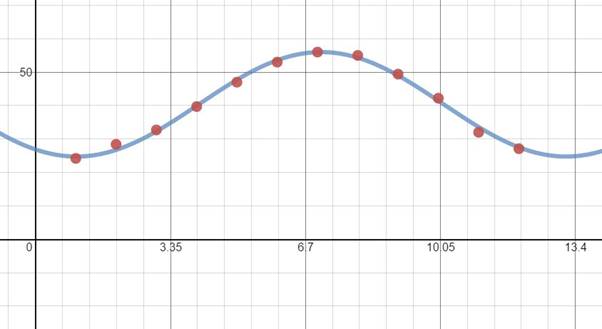
Figure 3