Precalculus
9th Edition
ISBN: 9780321716835
Author: Michael Sullivan
Publisher: Addison Wesley
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 6, Problem 54RE
To determine
Use the graph to determine domain and range of each function.
Expert Solution & Answer
Answer to Problem 54RE
Domain of function: 4tan(2x)={x∈R:2xπ+12∉Z}
Range of function: 4tan(2x)=(−∞,∞)
Explanation of Solution
Given information:
y=4tan(2x)
Graph of y=4tan(2x) :
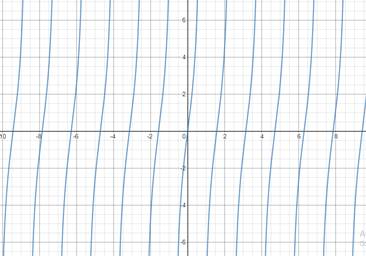
The Domain of the given function is {x∈R:2xπ+12∉Z}
As we can see from the above graph, it is continuous on every point, therefore the Range of graph will be all Real Numbers or (−∞,∞) .
Chapter 6 Solutions
Precalculus
Ch. 6.1 - What is the formula for the circumference C of a...Ch. 6.1 - If an object has a speed of r feet per second and...Ch. 6.1 - An angle is in _____ _____ if its vertex is at...Ch. 6.1 - A _____ _____ is a positive angle whose vertex is...Ch. 6.1 - If the radius of a circle is r and the length of...Ch. 6.1 - On a circle of radius r , a central angle of ...Ch. 6.1 - 180 = _____ radians a. 2 b. c. 3 2 d. 2Ch. 6.1 - An object travels on a circle of radius r with...Ch. 6.1 - True or False The angular speed of an object...Ch. 6.1 - True or False For circular motion on a circle of...
Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 11-22, draw each angle in standard...Ch. 6.1 - In Problems 23-34, convert each angle in degrees...Ch. 6.1 - In Problems 23-34, convert each angle in degrees...Ch. 6.1 - In Problems 23-34, convert each angle in degrees...Ch. 6.1 - In Problems 23-34, convert each angle in degrees...Ch. 6.1 - In Problems 23-34, convert each angle in degrees...Ch. 6.1 - In Problems 23-34, convert each angle in degrees...Ch. 6.1 - In Problems 23-34, convert each angle in degrees...Ch. 6.1 - In Problems 23-34, convert each angle in degrees...Ch. 6.1 - In Problems, convert each angle in degrees to...Ch. 6.1 - In Problems 23-34, convert each angle in degrees...Ch. 6.1 - In Problems 23-34, convert each angle in degrees...Ch. 6.1 - In Problems 23-34, convert each angle in degrees...Ch. 6.1 - In Problems 35—46, convert each angle in radians...Ch. 6.1 - In Problems 35—46, convert each angle in radians...Ch. 6.1 - In Problems 3546, convert each angle in...Ch. 6.1 - In Problems 35—46, convert each angle in radians...Ch. 6.1 - In Problems, convert each angle in radians to...Ch. 6.1 - In Problems 35—46, convert each angle in radians...Ch. 6.1 - In Problems 3546, convert each angle in...Ch. 6.1 - In Problems 35—46, convert each angle in radians...Ch. 6.1 - In Problems 35—46, convert each angle in radians...Ch. 6.1 - In Problems 35—46, convert each angle in radians...Ch. 6.1 - In Problems, convert each angle in radians to...Ch. 6.1 - In Problems 35—46, convert each angle in radians...Ch. 6.1 - In Problems 47-52, convert each angle in degrees...Ch. 6.1 - In Problems 47-52, convert each angle in degrees...Ch. 6.1 - In Problems 47-52, convert each angle in degrees...Ch. 6.1 - In Problems 47-52, convert each angle in degrees...Ch. 6.1 - In Problems 47-52, convert each angle in degrees...Ch. 6.1 - In Problems 47-52, convert each angle in degrees...Ch. 6.1 - In Problems 53-58, convert each angle in radians...Ch. 6.1 - In Problems 53-58, convert each angle in radians...Ch. 6.1 - In Problems 5358, convert each angle in radians to...Ch. 6.1 - In Problems 53-58, convert each angle in radians...Ch. 6.1 - In Problems 5358, convert each angle in radians to...Ch. 6.1 - Prob. 58AYUCh. 6.1 - In Problems 59-64, convert each angle to a decimal...Ch. 6.1 - In Problems 59-64, convert each angle to a decimal...Ch. 6.1 - Prob. 61AYUCh. 6.1 - Prob. 62AYUCh. 6.1 - In Problems 59-64, convert each angle to a decimal...Ch. 6.1 - Prob. 64AYUCh. 6.1 - In Problems 65-70, convert each angle to DMS form....Ch. 6.1 - In Problems 65-70, convert each angle to DMS form....Ch. 6.1 - In Problems 65-70, convert each angle to DMS form....Ch. 6.1 - In Problems 65-70, convert each angle to DMS form....Ch. 6.1 - In Problems 65-70, convert each angle to DMS form....Ch. 6.1 - In Problems 65-70, convert each angle to DMS form....Ch. 6.1 - In Problems 71-78, s denotes the length of the are...Ch. 6.1 - In Problems 71-78, s denotes the length of the are...Ch. 6.1 - In Problems 7178, s denotes the length of the arc...Ch. 6.1 - Prob. 74AYUCh. 6.1 - In Problems 7178, s denotes the length of the arc...Ch. 6.1 - In Problems 71-78, s denotes the length of the are...Ch. 6.1 - In Problems 71-78, s denotes the length of the are...Ch. 6.1 - In Problems 71-78, s denotes the length of the are...Ch. 6.1 - In Problems 79-86, A denotes the area of the...Ch. 6.1 - In Problems 79-86, A denotes the area of the...Ch. 6.1 - In Problems 79-86, A denotes the area of the...Ch. 6.1 - In Problems 79-86, A denotes the area of the...Ch. 6.1 - In Problems 79-86, A denotes the area of the...Ch. 6.1 - Prob. 84AYUCh. 6.1 - In Problems 79-86, A denotes the area of the...Ch. 6.1 - Prob. 86AYUCh. 6.1 - Prob. 87AYUCh. 6.1 - Prob. 88AYUCh. 6.1 - Prob. 89AYUCh. 6.1 - Prob. 90AYUCh. 6.1 - Movement of a Minute Hand The minute hand of a...Ch. 6.1 - Movement of a Pendulum A pendulum swings through...Ch. 6.1 - Area of a Sector Find the area of the sector of a...Ch. 6.1 - Area of a Sector Find the area of the sector of a...Ch. 6.1 - Watering a Lawn A water sprinkler sprays water...Ch. 6.1 - Designing a Water Sprinkler An engineer is asked...Ch. 6.1 - Prob. 97AYUCh. 6.1 - Prob. 98AYUCh. 6.1 - Prob. 99AYUCh. 6.1 - Prob. 101AYUCh. 6.1 - Prob. 102AYUCh. 6.1 - Prob. 103AYUCh. 6.1 - Prob. 104AYUCh. 6.1 - Prob. 105AYUCh. 6.1 - Prob. 106AYUCh. 6.1 - Prob. 107AYUCh. 6.1 - Prob. 108AYUCh. 6.1 - Prob. 109AYUCh. 6.1 - Prob. 110AYUCh. 6.1 - Prob. 111AYUCh. 6.1 - Prob. 112AYUCh. 6.1 - Prob. 113AYUCh. 6.1 - Prob. 100AYUCh. 6.1 - Prob. 115AYUCh. 6.1 - Prob. 116AYUCh. 6.1 - Prob. 117AYUCh. 6.1 - Prob. 118AYUCh. 6.1 - Prob. 123AYUCh. 6.1 - Prob. 124AYUCh. 6.1 - Prob. 119AYUCh. 6.1 - Prob. 120AYUCh. 6.1 - Prob. 121AYUCh. 6.1 - Prob. 122AYUCh. 6.1 - Prob. 114AYUCh. 6.1 - Prob. 125AYUCh. 6.2 - In a right triangle, with legs a and b and...Ch. 6.2 - The value of the function f( x )=3x7 at 5 is...Ch. 6.2 - True or False For a function y=f( x ) , for each x...Ch. 6.2 - If two triangles are similar, then corresponding...Ch. 6.2 - What point is symmetric with respect to the y-axis...Ch. 6.2 - Prob. 6AYUCh. 6.2 - Which function takes as input a real number t that...Ch. 6.2 - The point on the unit circle that corresponds to =...Ch. 6.2 - The point on the unit circle that corresponds to =...Ch. 6.2 - Prob. 12AYUCh. 6.2 - Prob. 11AYUCh. 6.2 - True or False Exact values can be found for the...Ch. 6.2 - In Problems 13-20, P=( x,y ) is the point on the...Ch. 6.2 - In Problems 13-20, P=( x,y ) is the point on the...Ch. 6.2 - In Problems 13-20, P=( x,y ) is the point on the...Ch. 6.2 - In Problems 13-20, P=( x,y ) is the point on the...Ch. 6.2 - In Problems 13-20, P=( x,y ) is the point on the...Ch. 6.2 - In Problems 13-20, P=( x,y ) is the point on the...Ch. 6.2 - In Problems 13-20, P=( x,y ) is the point on the...Ch. 6.2 - In Problems 13-20, P=( x,y ) is the point on the...Ch. 6.2 - In Problems 21-30, find the exact value. Do not...Ch. 6.2 - In Problems 21-30, find the exact value. Do not...Ch. 6.2 - In Problems 21-30, find the exact value. Do not...Ch. 6.2 - In Problems 21-30, find the exact value. Do not...Ch. 6.2 - In Problems 21-30, find the exact value. Do not...Ch. 6.2 - In Problems 21-30, find the exact value. Do not...Ch. 6.2 - In Problems 21-30, find the exact value. Do not...Ch. 6.2 - In Problems 21-30, find the exact value. Do not...Ch. 6.2 - In Problems 21-30, find the exact value. Do not...Ch. 6.2 - In Problems 21-30, find the exact value. Do not...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 31-46, find the exact value of each...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 47-64, find the exact values of the...Ch. 6.2 - In Problems 65-76, use a calculator to find the...Ch. 6.2 - In Problems 65-76, use a calculator to find the...Ch. 6.2 - In Problems 65-76, use a calculator to find the...Ch. 6.2 - In Problems 77-84, a point on the terminal side of...Ch. 6.2 - In Problems 77-84, a point on the terminal side of...Ch. 6.2 - In Problems 77-84, a point on the terminal side of...Ch. 6.2 - In Problems 77-84, a point on the terminal side of...Ch. 6.2 - In Problems 77-84, a point on the terminal side of...Ch. 6.2 - In Problems 77-84, a point on the terminal side of...Ch. 6.2 - In Problems 77-84, a point on the terminal side of...Ch. 6.2 - In Problems 77-84, a point on the terminal side of...Ch. 6.2 - Find the exact value of:...Ch. 6.2 - Find the exact value of: tan 60 +tan 150Ch. 6.2 - Find the exact value of: sin 40 +sin 130 +sin...Ch. 6.2 - Find the exact value of: tan 40 +tan 140Ch. 6.2 - If f( )=sin=0.1 , find f( + ) .Ch. 6.2 - If f( )=cos=0.3 , find f( + ) .Ch. 6.2 - If f( )=tan=3 , find f( + ) .Ch. 6.2 - If f( )=cot=2 , find f( + ) .Ch. 6.2 - If sin= 1 5 , find csc .Ch. 6.2 - If cos= 2 3 , find sec .Ch. 6.2 - In Problems 95-106, f( )=sin and g( )=cos . Find...Ch. 6.2 - In Problems 95-106, f( )=sin and g( )=cos . Find...Ch. 6.2 - In Problems 95-106, f( )=sin and g( )=cos . Find...Ch. 6.2 - In Problems 95-106, f( )=sin and g( )=cos . Find...Ch. 6.2 - In Problems 95-106, f( )=sin and g( )=cos . Find...Ch. 6.2 - In Problems 95-106, f( )=sin and g( )=cos . Find...Ch. 6.2 - In Problems 95-106, f( )=sin and g( )=cos . Find...Ch. 6.2 - In Problems 95-106, f( )=sin and g( )=cos . Find...Ch. 6.2 - In Problems 95-106, f( )=sin and g( )=cos . Find...Ch. 6.2 - In Problems 95-106, f( )=sin and g( )=cos . Find...Ch. 6.2 - Prob. 105AYUCh. 6.2 - Prob. 106AYUCh. 6.2 - In Problems 107-116, f( x )=sinx , g( x )=cosx ,...Ch. 6.2 - Prob. 108AYUCh. 6.2 - In Problems 107-116, f( x )=sinx , g( x )=cosx ,...Ch. 6.2 - Prob. 110AYUCh. 6.2 - In Problems 107-116, f( x )=sinx , g( x )=cosx ,...Ch. 6.2 - Prob. 112AYUCh. 6.2 - Prob. 113AYUCh. 6.2 - Prob. 114AYUCh. 6.2 - In Problems 107-116, f( x )=sinx , g( x )=cosx ,...Ch. 6.2 - In Problems 107-116, f( x )=sinx , g( x )=cosx ,...Ch. 6.2 - Find two negative and three positive angles,...Ch. 6.2 - Find two negative and three positive angles,...Ch. 6.2 - Prob. 119AYUCh. 6.2 - Use a calculator in radian mode to complete the...Ch. 6.2 - Prob. 121AYUCh. 6.2 - For Problems 121-124, use the following...Ch. 6.2 - For Problems 121-124, use the following...Ch. 6.2 - For Problems 121-124, use the following...Ch. 6.2 - Prob. 125AYUCh. 6.2 - Prob. 126AYUCh. 6.2 - Prob. 127AYUCh. 6.2 - Prob. 128AYUCh. 6.2 - Prob. 129AYUCh. 6.2 - Prob. 130AYUCh. 6.2 - Prob. 131AYUCh. 6.2 - Prob. 132AYUCh. 6.2 - Prob. 133AYUCh. 6.2 - Prob. 134AYUCh. 6.2 - Prob. 135AYUCh. 6.3 - The domain of the function f(x)= x+1 2x+1 is _____...Ch. 6.3 - A function for which f(x)=f(x) for all x in the...Ch. 6.3 - True or False The function f(x)= x is even....Ch. 6.3 - True or False The equation x 2 +2x= (x+1) 2 1 is...Ch. 6.3 - The sine, cosine, cosecant, and secant functions...Ch. 6.3 - The domain of the tangent function is _____ .Ch. 6.3 - Which of the following is not in the range of the...Ch. 6.3 - Which of the following functions is even? a....Ch. 6.3 - sin 2 + cos 2 = _____ .Ch. 6.3 - True or False sec= 1 sinCh. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - ln Problems 11-26, use the fact that the...Ch. 6.3 - In Problems 27—34, name the quadrant in which...Ch. 6.3 - In Problems 27—34, name the quadrant in which...Ch. 6.3 - In Problems 27—34, name the quadrant in which...Ch. 6.3 - In Problems 27—34, name the quadrant in which...Ch. 6.3 - In Problems 27—34, name the quadrant in which...Ch. 6.3 - In Problems 27—34, name the quadrant in which...Ch. 6.3 - In Problems 27—34, name the quadrant in which...Ch. 6.3 - Prob. 34AYUCh. 6.3 - In problems 35-42, sin and cos are given. Find the...Ch. 6.3 - In problems 35-42, sin and cos are given. Find the...Ch. 6.3 - In problems 35-42, sin and cos are given. Find the...Ch. 6.3 - In problems 35-42, sin and cos are given. Find the...Ch. 6.3 - In problems 35-42, sin and cos are given. Find the...Ch. 6.3 - In problems 35-42, sin and cos are given. Find the...Ch. 6.3 - In problems 35-42, sin and cos are given. Find the...Ch. 6.3 - In problems 35-42, sin and cos are given. Find the...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 43-58, find the exact value of each of...Ch. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - Prob. 66AYUCh. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - Prob. 68AYUCh. 6.3 - Prob. 69AYUCh. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - Prob. 72AYUCh. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - In Problems 59-76, use the even-odd properties to...Ch. 6.3 - Prob. 76AYUCh. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - In Problems 77-88, use properties of the...Ch. 6.3 - If sin=0.3 , find the value of: sin+sin( +2 )+sin(...Ch. 6.3 - If cos=0.2 , find the value of: cos+cos( +2 )+cos(...Ch. 6.3 - If tan=3 , find the value of: tan+tan( + )+tan( +2...Ch. 6.3 - If cot=2 , find the value of: cot+cot( - )+cot( -2...Ch. 6.3 - Find the exact value of: sin 1 + sin2 + sin3 ++...Ch. 6.3 - Find the exact value of: cos 1 + cos2 + cos3 ++...Ch. 6.3 - What is the domain of the sine function?Ch. 6.3 - What is the domain of the cosine function?Ch. 6.3 - For what numbers is f( )=tan not defined?Ch. 6.3 - For what numbers is f( )=cot not defined?Ch. 6.3 - For what numbers is f( )=sec not defined?Ch. 6.3 - For what numbers is f( )=csc not defined?Ch. 6.3 - What is the range of the sine function?Ch. 6.3 - What is the range of the cosine function?Ch. 6.3 - What is the range of the tangent function?Ch. 6.3 - What is the range of the cotangent function?Ch. 6.3 - What is the range of the secant function?Ch. 6.3 - What is the range of the cosecant function?Ch. 6.3 - Is the sine function even, odd, or neither? Is its...Ch. 6.3 - Is the cosine function even, odd, or neither? Is...Ch. 6.3 - Is the tangent function even, odd, or neither? Is...Ch. 6.3 - Is the cotangent function even, odd, or neither?...Ch. 6.3 - Is the cotangent function even, odd, or neither?...Ch. 6.3 - Is the cotangent function even, odd, or neither?...Ch. 6.3 - In Problems 113-118, use the periodic and even-odd...Ch. 6.3 - In Problems 113-118, use the periodic and even-odd...Ch. 6.3 - In Problems 113-118, use the periodic and even-odd...Ch. 6.3 - In Problems 113-118, use the periodic and even-odd...Ch. 6.3 - In Problems 113-118, use the periodic and even-odd...Ch. 6.3 - In Problems 113-118, use the periodic and even-odd...Ch. 6.3 - Calculating the Time of a Trip From a parking lot,...Ch. 6.3 - Calculating the Time of a Trip Two oceanfront...Ch. 6.3 - Prob. 121AYUCh. 6.3 - Prob. 122AYUCh. 6.3 - Prob. 123AYUCh. 6.3 - Prob. 124AYUCh. 6.3 - Prob. 125AYUCh. 6.3 - Prob. 126AYUCh. 6.3 - Prob. 127AYUCh. 6.3 - Prob. 128AYUCh. 6.3 - Prob. 129AYUCh. 6.3 - Prob. 130AYUCh. 6.3 - Prob. 131AYUCh. 6.3 - Prob. 132AYUCh. 6.3 - Prob. 133AYUCh. 6.3 - Prob. 134AYUCh. 6.3 - Prob. 135AYUCh. 6.3 - Prob. 136AYUCh. 6.4 - Use transformations to graph y=3 x 2 . (pp....Ch. 6.4 - Use transformations to graph y= 2x . (pp. 106-114)Ch. 6.4 - The maximum value of y=sinx , 0x2 , is ____ and...Ch. 6.4 - The function y=Asin( x ) , A0 ,has amplitude 3 and...Ch. 6.4 - The function y=3cos( 6x ) has amplitude ____ and...Ch. 6.4 - True or False The graphs of y=sinx and y=cosx are...Ch. 6.4 - True or false For y=2sin( x ) , the amplitude is 2...Ch. 6.4 - True or False The graph of the sine function has...Ch. 6.4 - f( x )=sinx (a) What is the y-intercept of the...Ch. 6.4 - g( x )=cosx (a) What is the y-intercept of the...Ch. 6.4 - Prob. 11AYUCh. 6.4 - Prob. 12AYUCh. 6.4 - Prob. 13AYUCh. 6.4 - Prob. 14AYUCh. 6.4 - Prob. 15AYUCh. 6.4 - Prob. 16AYUCh. 6.4 - Prob. 17AYUCh. 6.4 - Prob. 18AYUCh. 6.4 - Prob. 19AYUCh. 6.4 - Prob. 20AYUCh. 6.4 - In Problems 23-32, match the given function to one...Ch. 6.4 - In Problems 23-32, match the given function to one...Ch. 6.4 - In Problems 23-32, match the given function to one...Ch. 6.4 - In Problems 23-32, match the given function to one...Ch. 6.4 - In Problems 23-32, match the given function to one...Ch. 6.4 - In Problems 23-32, match the given function to one...Ch. 6.4 - In Problems 23-32, match the given function to one...Ch. 6.4 - In Problems 23-32, match the given function to one...Ch. 6.4 - In Problems 23-32, match the given function to one...Ch. 6.4 - In Problems 23-32, match the given function to one...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 33-56, graph each function using...Ch. 6.4 - In Problems 57-60, write the equation of a sine...Ch. 6.4 - In Problems 57-60, write the equation of a sine...Ch. 6.4 - In Problems 57-60, write the equation of a sine...Ch. 6.4 - In Problems 57-60, write the equation of a sine...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 61-74, find an equation for each...Ch. 6.4 - In Problems 75-78, find the average rate of change...Ch. 6.4 - In Problems 75-78, find the average rate of change...Ch. 6.4 - In Problems 75-78, find the average rate of change...Ch. 6.4 - In Problems 75-78, find the average rate of change...Ch. 6.4 - In Problems 79-82, find ( fg ) (x) and (gf) ( x )...Ch. 6.4 - Prob. 78AYUCh. 6.4 - Prob. 79AYUCh. 6.4 - Prob. 80AYUCh. 6.4 - Prob. 81AYUCh. 6.4 - Prob. 82AYUCh. 6.4 - Prob. 83AYUCh. 6.4 - Prob. 84AYUCh. 6.4 - Prob. 85AYUCh. 6.4 - Prob. 86AYUCh. 6.4 - Alternating Current (ac) Circuits The current I ,...Ch. 6.4 - Alternating Current (ac) Circuits The current I ,...Ch. 6.4 - Prob. 89AYUCh. 6.4 - Prob. 90AYUCh. 6.4 - Prob. 91AYUCh. 6.4 - Prob. 92AYUCh. 6.4 - Prob. 93AYUCh. 6.4 - Prob. 94AYUCh. 6.4 - Prob. 95AYUCh. 6.4 - Prob. 97AYUCh. 6.4 - Prob. 96AYUCh. 6.4 - Prob. 98AYUCh. 6.4 - Prob. 99AYUCh. 6.4 - Prob. 100AYUCh. 6.4 - Prob. 101AYUCh. 6.4 - Prob. 102AYUCh. 6.4 - Prob. 103AYUCh. 6.4 - Prob. 104AYUCh. 6.4 - Prob. 105AYUCh. 6.4 - Prob. 106AYUCh. 6.4 - Prob. 107AYUCh. 6.4 - Prob. 108AYUCh. 6.5 - The graph of y= 3x6 x4 has a vertical asymptote....Ch. 6.5 - True or False If x=3 is a vertical asymptote of a...Ch. 6.5 - The graph of y=tanx is symmetric with respect to...Ch. 6.5 - The graph of y=secx is symmetric with respect to...Ch. 6.5 - It is easiest to graph y=secx by first sketching...Ch. 6.5 - True or False The graphs of...Ch. 6.5 - In Problems 7-16, if necessary, refer to the...Ch. 6.5 - In Problems 7-16, if necessary, refer to the...Ch. 6.5 - In Problems 7-16, if necessary, refer to the...Ch. 6.5 - In Problems 7-16, if necessary, refer to the...Ch. 6.5 - In Problems 7-16, if necessary, refer to the...Ch. 6.5 - In Problems 7-16, if necessary, refer to the...Ch. 6.5 - In Problems 7-16, if necessary, refer to the...Ch. 6.5 - In Problems 7-16, if necessary, refer to the...Ch. 6.5 - In Problems 7-16, if necessary, refer to the...Ch. 6.5 - In Problems 7-16, if necessary, refer to the...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 17-40, graph each function. Be sure to...Ch. 6.5 - In Problems 41-44, find the average rale of change...Ch. 6.5 - In Problems 41-44, find the average rale of change...Ch. 6.5 - In Problems 41-44, find the average rale of change...Ch. 6.5 - In Problems 41-44, find the average rale of change...Ch. 6.5 - In Problems 45-48, find ( fg )( x )and( gf )( x )...Ch. 6.5 - In Problems 45-48, find ( fg )( x )and( gf )( x )...Ch. 6.5 - In Problems 45-48, find ( fg )( x )and( gf )( x )...Ch. 6.5 - In Problems 45-48, find ( fg )( x )and( gf )( x )...Ch. 6.5 - In Problems 49 and 50, graph each function. f( x...Ch. 6.5 - In Problems 49 and 50, graph each function. g( x...Ch. 6.5 - Carrying a Ladder around a Corner Two hallways,...Ch. 6.5 - A Rotating Beacon Suppose that a fire truck is...Ch. 6.5 - Exploration Graph y=tanxandy=cot( x+ 2 ) Do you...Ch. 6.6 - For the graph of y=Asin( x ) , the number is...Ch. 6.6 - True or False A graphing utility requires only two...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 3-14, find the amplitude, period, and...Ch. 6.6 - In Problems 15-18, write the equation of a sine...Ch. 6.6 - In Problems 15-18, write the equation of a sine...Ch. 6.6 - In Problems 15-18, write the equation of a sine...Ch. 6.6 - In Problems 15-18, write the equation of a sine...Ch. 6.6 - Prob. 19AYUCh. 6.6 - Prob. 20AYUCh. 6.6 - Prob. 21AYUCh. 6.6 - Prob. 22AYUCh. 6.6 - Prob. 23AYUCh. 6.6 - Prob. 24AYUCh. 6.6 - Prob. 25AYUCh. 6.6 - Prob. 26AYUCh. 6.6 - Prob. 27AYUCh. 6.6 - Prob. 28AYUCh. 6.6 - Prob. 29AYUCh. 6.6 - Prob. 30AYUCh. 6.6 - Prob. 31AYUCh. 6.6 - Prob. 32AYUCh. 6.6 - Prob. 33AYUCh. 6.6 - Prob. 34AYUCh. 6.6 - Prob. 35AYUCh. 6.6 - Prob. 36AYUCh. 6.6 - Prob. 37AYUCh. 6.6 - Prob. 38AYUCh. 6.6 - Prob. 39AYUCh. 6.6 - Prob. 40AYUCh. 6 - Prob. 1RECh. 6 - Prob. 2RECh. 6 - Prob. 3RECh. 6 - Prob. 4RECh. 6 - Prob. 5RECh. 6 - Prob. 6RECh. 6 - Prob. 7RECh. 6 - Prob. 8RECh. 6 - Prob. 9RECh. 6 - Prob. 10RECh. 6 - Prob. 11RECh. 6 - Prob. 12RECh. 6 - Prob. 13RECh. 6 - Prob. 14RECh. 6 - Prob. 15RECh. 6 - Prob. 16RECh. 6 - Prob. 17RECh. 6 - Prob. 18RECh. 6 - Prob. 19RECh. 6 - Prob. 20RECh. 6 - Prob. 21RECh. 6 - Prob. 22RECh. 6 - Prob. 23RECh. 6 - Prob. 24RECh. 6 - Prob. 25RECh. 6 - Prob. 26RECh. 6 - Prob. 27RECh. 6 - Prob. 28RECh. 6 - Prob. 29RECh. 6 - Prob. 30RECh. 6 - Prob. 31RECh. 6 - Prob. 32RECh. 6 - Prob. 33RECh. 6 - Prob. 34RECh. 6 - Prob. 35RECh. 6 - Prob. 36RECh. 6 - Prob. 37RECh. 6 - Prob. 38RECh. 6 - Prob. 39RECh. 6 - Prob. 40RECh. 6 - Prob. 41RECh. 6 - Prob. 42RECh. 6 - Prob. 43RECh. 6 - Prob. 44RECh. 6 - Prob. 45RECh. 6 - Prob. 46RECh. 6 - Prob. 47RECh. 6 - Prob. 48RECh. 6 - Prob. 49RECh. 6 - Prob. 50RECh. 6 - Prob. 51RECh. 6 - Prob. 52RECh. 6 - Prob. 53RECh. 6 - Prob. 54RECh. 6 - Prob. 55RECh. 6 - Prob. 56RECh. 6 - Prob. 57RECh. 6 - Prob. 58RECh. 6 - Prob. 59RECh. 6 - Prob. 60RECh. 6 - Prob. 61RECh. 6 - Prob. 62RECh. 6 - Prob. 63RECh. 6 - Prob. 64RECh. 6 - Prob. 65RECh. 6 - Prob. 66RECh. 6 - Prob. 67RECh. 6 - Prob. 68RECh. 6 - Prob. 69RECh. 6 - Prob. 70RECh. 6 - Prob. 71RECh. 6 - Prob. 72RECh. 6 - Prob. 73RECh. 6 - Prob. 74RECh. 6 - Prob. 75RECh. 6 - Prob. 76RECh. 6 - Prob. 77RECh. 6 - Prob. 78RECh. 6 - Prob. 79RECh. 6 - Prob. 80RECh. 6 - Prob. 81RECh. 6 - Prob. 82RECh. 6 - Prob. 83RECh. 6 - Prob. 84RECh. 6 - Prob. 85RECh. 6 - Prob. 86RECh. 6 - Prob. 87RECh. 6 - Prob. 88RECh. 6 - Prob. 89RECh. 6 - Prob. 90RECh. 6 - Prob. 91RECh. 6 - Prob. 92RECh. 6 - Prob. 93RECh. 6 - Prob. 94RECh. 6 - Prob. 95RECh. 6 - Prob. 96RECh. 6 - Prob. 97RECh. 6 - In Problem, convert each angle in degrees to...Ch. 6 - In Problem 13, convert each angle in degrees to...Ch. 6 - In problem 13, convert each angle in degrees to...Ch. 6 - In Problem 46, convert each angle in radius to...Ch. 6 - In Problem, convert each angle in radius to...Ch. 6 - In Problem, convert each angle in radius to...Ch. 6 - In Problem 712, find the exact value of each...Ch. 6 - In Problem 712, find the exact value of each...Ch. 6 - In Problem 712, find the exact value of each...Ch. 6 - In Problem, find the exact value of each...Ch. 6 - In Problem 712, find the exact value of each...Ch. 6 - Prob. 12CTCh. 6 - Prob. 13CTCh. 6 - In Problem 1316, use a calculator to evaluate each...Ch. 6 - Prob. 15CTCh. 6 - Prob. 16CTCh. 6 - 17. Fill in each table entry with sign of each...Ch. 6 - 18. If and, find.
Ch. 6 - In Problems 1921, find the value of the remaining...Ch. 6 - Prob. 20CTCh. 6 - In Problems 1921, find the value of the remaining...Ch. 6 - In Problems, the point is on the terminal side of...Ch. 6 - In Problems, the point is on the terminal side of...Ch. 6 - In Problems 2224, the point (x,y) is on the...Ch. 6 - In Problems and, graph the function.
25.
Ch. 6 - In Problems and, graph the function.
25.
Ch. 6 - Write an equation for a sinusoidal graph with the...Ch. 6 - Logan has a garden in the shape of a sector of a...Ch. 6 - Hungarian Adrian Annus won the gold medal for the...Ch. 6 - Find the real solutions, if any, of the equation
Ch. 6 - 2. Find an equation for the line with slope ...Ch. 6 - Prob. 3CRCh. 6 - 4. Describe the equation. Graph it.
Ch. 6 - 5. Describe the equation Graph it.
Ch. 6 - 6. Use the transformation to graph the function
Ch. 6 - 7. Sketch a graph of each of the following...Ch. 6 - Find the inverse function of f(x)=3x2Ch. 6 - 9. Find the exact value of.
Ch. 6 - Graph y=3sin(2x).Ch. 6 - 11. Find the exact value of.
Ch. 6 - 12. Find an exponential function for the following...Ch. 6 - 13. Find a sinusoidal function for the following...Ch. 6 - 14.
(a) Find a linear function that contains the...Ch. 6 - (a) Find a polynomial function of degree 3 whose...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Find the volumes of the regions in Exercises 23–36.
26. The wedge cut from the cylinder by the planes and
University Calculus: Early Transcendentals (4th Edition)
4. You construct a 95% confidence interval for a population mean using a random sample. The confidence interval...
Elementary Statistics: Picturing the World (7th Edition)
The representation of the equation −2x+5y=10 is either linear or non-linear is to be analyze.
Pre-Algebra Student Edition
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
Twenty workers are to be assigned to 20 different jobs, one to each job. How many different assignments are pos...
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 15A cylindrical tank with radius 8 m is being filled with water at a rate of 2 m³/min. What is the rate of change of the water height in this tank? 6)A box with a square base and an open top must box that will minimiarrow_forward#12 The radius of a sphere increases at a rate of 3 in/sec. How fast is the volume increasing when the diameter is 24arrow_forward84 256 cubic inches. Find the dimensions of the of material used (the surface area). A farmer wishes to enclose a rectangular plot using 200 m of fencing material. One side of the land borders a river and does not need fencing. What is the largest area that can be enclosed? For the function y=x³-3x²-1, use derivatives to: 3 b) 2x - 6x2 (a) determine the intarrow_forward
- Can you solve this 6 questions numerical method and teach me how to solve it and what we use.arrow_forward9Wire of length 20m is divided into two pieces and the pieces are bent into a square and a circle. How should this be done in order to minimize the sum of their areas? Round your answer to the nearest hundredth.arrow_forwardUse Laplace transform to solve the initial value problem y' + y = tsin(t), y(0) = 0arrow_forward
- The function g is defined by g(x) = sec² x + tan x. What are all solutions to g(x) = 1 on the interval 0 ≤ x ≤ 2π ? A x = = 0, x == = 3, x = π, x = 7 4 , 4 and x 2π only = B x = 4' 1, x = 1, x = 57 and x = 3 only C x = πk and x = - +πk D , where is any integer П x = +πk and П x = +πk, where k is any integerarrow_forwardVector v = PQ has initial point P (2, 14) and terminal point Q (7, 3). Vector v = RS has initial point R (29, 8) and terminal point S (12, 17). Part A: Write u and v in linear form. Show all necessary work. Part B: Write u and v in trigonometric form. Show all necessary work. Part C: Find 7u − 4v. Show all necessary calculations.arrow_forwardAn object is suspended by two cables attached at a single point. The force applied on one cable has a magnitude of 125 pounds and acts at an angle of 37°. The force on the other cable is 75 pounds at an angle of 150°.Part A: Write each vector in component form. Show all necessary work.Part B: Find the dot product of the vectors. Show all necessary calculations Part C: Use the dot product to find the angle between the cables. Round the answer to the nearest degree. Show all necessary calculations.arrow_forward
- An airplane flies at 500 mph with a direction of 135° relative to the air. The plane experiences a wind that blows 60 mph with a direction of 60°.Part A: Write each of the vectors in linear form. Show all necessary calculations.Part B: Find the sum of the vectors. Show all necessary calculations. Part C: Find the true speed and direction of the airplane. Round the speed to the thousandths place and the direction to the nearest degree. Show all necessary calculations.arrow_forwardUse sigma notation to write the sum. Σ EM i=1 - n 2 4n + n narrow_forwardVectors t = 3i + 7j, u = 2i − 5j, and v = −21i + 9j are given.Part A: Find the angle between vectors t and u. Show all necessary calculations. Part B: Choose a value for c, such that c > 1. Find w = cv. Show all necessary work.Part C: Use the dot product to determine if t and w are parallel, orthogonal, or neither. Justify your answer.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Inverse Functions; Author: Professor Dave Explains;https://www.youtube.com/watch?v=9fJsrnE1go0;License: Standard YouTube License, CC-BY