Chapter 6, Problem 96RE

(a)

To determine

To find: The sinusoidal function.

Answer to Problem 96RE

The sinusoidal function is $y=2.465\sin \left(\frac{2\pi }{356}x-1.39\right)+12.165$ .

Explanation of Solution

Given;

The number of hours on the Summer solstice is 14.63

The number of sunlight on the winter solstice is 9.72

Calculation:

The amplitude is calculated as,

  $\begin{array}{c}A=\frac{\text{largest value}-\text{smallest value}}{2}\\ =\frac{14.63-9.70}{2}\\ =2.465\end{array}$

The vertical shift is calculated as,

  $\begin{array}{c}\text{Vertical shift}=\frac{\text{largest value}+\text{smallest value}}{2}\\ =\frac{14.63+9.70}{2}\\ =12.165\end{array}$

The days are 365.

Write the sinusoidal equation in the form.

  $y=2.465\sin \left(\frac{2\pi }{356}x-\varphi \right)+12.165$

Calculate $\varphi$ .

  $\begin{array}{c}\varphi =172-91.25\\ =80.75\end{array}$

Write the sinusoidal equation in the form.

  $y=2.465\sin \left(\frac{2\pi }{356}x-80.75\right)+12.165$

Solve further as,

  $\begin{array}{c}y=2.465\sin \left(\frac{2\pi }{356}x-\frac{2\pi \left(80.75\right)}{365}\right)+12.165\\ =2.465\sin \left(\frac{2\pi }{356}x-1.39\right)+12.165\end{array}$

Thus, the sinusoidal function is $y=2.465\sin \left(\frac{2\pi }{356}x-1.39\right)+12.165$ .

(b)

To determine

To find: The number of hours of sunlight on April 1.

Answer to Problem 96RE

The number of hours of sunlight on April 1 is 12.6

Explanation of Solution

Substitute 91 for x in $y=2.465\sin \left(\frac{2\pi }{356}x-1.39\right)+12.165$ .

  $\begin{array}{c}y=2.465\sin \left(\frac{2\pi }{356}\left(91\right)-1.39\right)+12.165\\ =12.6\end{array}$

Thus, the number of hours of sunlight on April 1 is 12.6

(c)

To determine

To find: The graph for the function.

Answer to Problem 96RE

The graph for the function is shown in figure 1.

Explanation of Solution

The graph is drawn as,

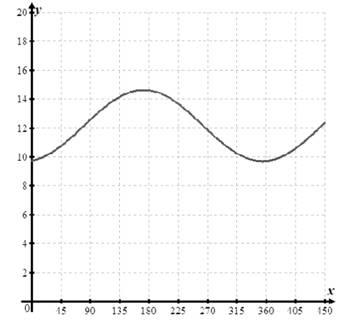
Figure 1

Thus, the graph for the function is shown in figure 1.

(d)

To determine

To find: The comparison of the actual hours of day light.

Answer to Problem 96RE

The hours are same as the predicted time.

Explanation of Solution

The total number of hours is 12.6 of sunlight on April 1 according to the Old Farmers Almanac. The above hours are same as the predicted time.

Thus, the hours are same as the predicted time.