Chapter 6.5, Problem 31AYU

In Problems 17-40, graph each function. Be sure to label key points and show at least two cycles. Use the graph to determine the domain and the range of each function.

$y=-2\csc \left(\pi x\right)$

To determine

To find: Domain and range.

Answer to Problem 31AYU

Solution:

Domain is $\left\{x\text{|}x\ne k,k\text{ is an integer}\right\}$.

Range $\left\{y\text{|}y\le -2\text{ or }y\ge 2\right\}$.

Explanation of Solution

Given:

$y=-2\csc \left(\pi x\right)$

Calculation:

The graph $y=-2\csc \left(\pi x\right)$.

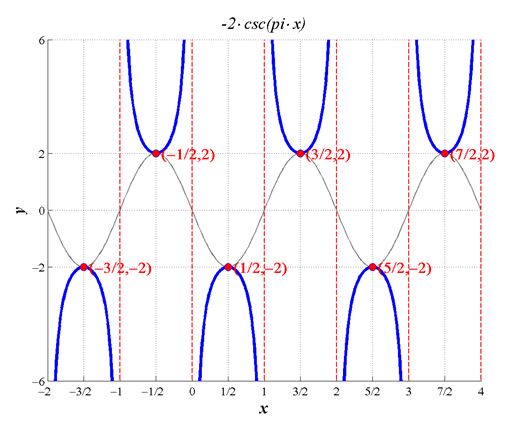
By the graph we determine that the domain of this function is the set of all real numbers where cosecant is defined, which excludes points $x$ where vertical asymptotes occur. Since $-2\csc \left(\pi x\right)=\frac{-2}{\sin \left(\pi x\right)}$ this happens when $\text{sin}\left(\pi x\right)=0\Rightarrow \pi x=k\pi \Rightarrow x=k$. Therefore the domain is $\left\{x\text{|}x\ne k,k\text{ is an integer}\right\}$. To determine the range we take note of the value of $A=-2$, which will scale the underlying reciprocal sine function amplitude to 2. The given function $-2\csc \left(\pi x\right)$ will not enter into the space of the cosine $y=-2\csc \left(\pi x\right)$ (apart from its maxima and minima). Therefore the range is $\left\{y\text{|}y\le -2\text{ or }y\ge 2\right\}$. This agrees with the graph provided.

Therefore the,

Domain is $\left\{x\text{|}x\ne k,k\text{ is an integer}\right\}$.

Range $\left\{y\text{|}y\le -2\text{ or }y\ge 2\right\}$.