Fox And Mcdonald's Introduction To Fluid Mechanics
9th Edition
ISBN: 9781118921876
Author: Pritchard, Philip J.; Leylegian, John C.; Bhaskaran, Rajesh
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5, Problem 62P
Consider again the viscometric flow of Example 5.7. Evaluate the average rate of rotation of a pair of perpendicular line segments oriented at ±45° from the x axis. Show that this is the same as in the example.
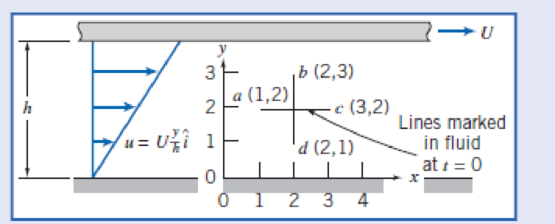
Example 5.7 ROTATION IN VISCOMETRIC FLOW
A viscometric flow in the narrow gap between large parallel plates is shown. The velocity field in the narrow gap is given by
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
velocity field is given by:
A two-dimensional
V = (x - 2y) i- (2x + y)Ĵj
a. Show that the flow is incompressible and irrotational.
b. Derive the expression for the velocity potential, (x,y).
c. Derive the expression for the stream function, 4(x,y).
Please answer with detail
1. For a velocity field described by V = 2x2i − zyk, is the flow two- or threedimensional? Incompressible? 2. For an Eulerian flow field described by u = 2xyt, v = y3x/3, w = 0, find the slope of the streamline passing through the point [2, 4] at t = 2. 3. Find the angle the streamline makes with the x-axis at the point [-1, 0.5] for the velocity field described by V = −xyi + 2y2j
Chapter 5 Solutions
Fox And Mcdonald's Introduction To Fluid Mechanics
Ch. 5 - Which of the following sets of equations represent...Ch. 5 - Which of the following sets of equations represent...Ch. 5 - In an incompressible three-dimensional flow field,...Ch. 5 - In a two-dimensional incompressible flow field,...Ch. 5 - The three components of velocity in a velocity...Ch. 5 - The x component of velocity in a steady,...Ch. 5 - The y component of velocity in a steady...Ch. 5 - The velocity components for an incompressible...Ch. 5 - The radial component of velocity in an...Ch. 5 - A crude approximation for the x component of...
Ch. 5 - A useful approximation for the x component of...Ch. 5 - A useful approximation for the x component of...Ch. 5 - For a flow in the xy plane, the x component of...Ch. 5 - Consider a water stream from a jet of an...Ch. 5 - Which of the following sets of equations represent...Ch. 5 - For an incompressible flow in the r plane, the r...Ch. 5 - A viscous liquid is sheared between two parallel...Ch. 5 - A velocity field in cylindrical coordinates is...Ch. 5 - Determine the family of stream functions that...Ch. 5 - The stream function for a certain incompressible...Ch. 5 - Determine the stream functions for the following...Ch. 5 - Determine the stream function for the steady...Ch. 5 - Prob. 23PCh. 5 - A parabolic velocity profile was used to model...Ch. 5 - A flow field is characterized by the stream...Ch. 5 - A flow field is characterized by the stream...Ch. 5 - Prob. 27PCh. 5 - A flow field is characterized by the stream...Ch. 5 - In a parallel one-dimensional flow in the positive...Ch. 5 - Consider the flow field given by V=xy2i13y3j+xyk....Ch. 5 - Prob. 31PCh. 5 - The velocity field within a laminar boundary layer...Ch. 5 - A velocity field is given by V=10ti10t3j. Show...Ch. 5 - The y component of velocity in a two-dimensional,...Ch. 5 - A 4 m diameter tank is filled with water and then...Ch. 5 - An incompressible liquid with negligible viscosity...Ch. 5 - Sketch the following flow fields and derive...Ch. 5 - Consider the low-speed flow of air between...Ch. 5 - As part of a pollution study, a model...Ch. 5 - As an aircraft flies through a cold front, an...Ch. 5 - Wave flow of an incompressible fluid into a solid...Ch. 5 - A steady, two-dimensional velocity field is given...Ch. 5 - A velocity field is represented by the expression...Ch. 5 - A parabolic approximate velocity profile was used...Ch. 5 - A cubic approximate velocity profile was used in...Ch. 5 - The velocity field for steady inviscid flow from...Ch. 5 - Consider the incompressible flow of a fluid...Ch. 5 - Consider the one-dimensional, incompressible flow...Ch. 5 - Expand (V)V in cylindrical coordinates by direct...Ch. 5 - Determine the velocity potential for (a) a flow...Ch. 5 - Determine whether the following flow fields are...Ch. 5 - The velocity profile for steady flow between...Ch. 5 - Consider the velocity field for flow in a...Ch. 5 - Consider the two-dimensional flow field in which u...Ch. 5 - Consider a flow field represented by the stream...Ch. 5 - Fluid passes through the set of thin, closely...Ch. 5 - A two-dimensional flow field is characterized as u...Ch. 5 - A flow field is represented by the stream function...Ch. 5 - Consider the flow field represented by the stream...Ch. 5 - Consider the flow field represented by the stream...Ch. 5 - Consider the velocity field given by V=Ax2i+Bxyj,...Ch. 5 - Consider again the viscometric flow of Example...Ch. 5 - The velocity field near the core of a tornado can...Ch. 5 - A velocity field is given by V=2i4xjm/s. Determine...Ch. 5 - Consider the pressure-driven flow between...Ch. 5 - Consider a steady, laminar, fully developed,...Ch. 5 - Assume the liquid film in Example 5.9 is not...Ch. 5 - Consider a steady, laminar, fully developed...Ch. 5 - Consider a steady, laminar, fully developed...Ch. 5 - A linear velocity profile was used to model flow...Ch. 5 - A cylinder of radius ri rotates at a speed ...Ch. 5 - The velocity profile for fully developed laminar...Ch. 5 - Assume the liquid film in Example 5.9 is...Ch. 5 - The common thermal polymerase chain reaction (PCR)...Ch. 5 - A tank contains water (20C) at an initial depth y0...Ch. 5 - For a small spherical particle of styrofoam...Ch. 5 - Use Excel to generate the progression to an...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A viscous incompressible liquid of density p and of dynamic viscosity n is carried upwards against gravity with the aid of moving side walls. This laminar flow is steady and fully developed in z-direction and there is no applied pressure gradient. The coordinate is fixed in the midway between the walls as shown below. 2d g=-gk liquid P, n x=-d x=d I. The velocity profile in z-direction is pg w(x) = (x2 – d) + U. 2n II. To be able to carry a net amount of liquid upwards, the wall velocities need to be greater than pgd²/(2n). III. If one of the walls stops, increasing the speed of the other wall to 3/2U would carry the same amount of liquid upwards. Which of the above statements are true?arrow_forwardConsider the flow field V = (ay+dx)i + (bx-dy)j + ck, where a(t), b(t), c(t), and d(t) are time dependent coefficients. Prove the density is constant following a fluid particle, then find the pressure gradient vector gradP, Γ for a circular contour of radius R in the x-y plane (centered on the origin) using a contour integral, and Γ by evaluating the Stokes theorem surface integral on the hemisphere of radius R above the x-y plane bounded by the contour.arrow_forwardThe velocity components for a three dimensional incornpressible flow is given by : u=x° -y-z'x, v=y' -z 3 w = - 3x'z - 3y'z + Check whether the flow satisfies continuity ?arrow_forward
- A fluid has a velocity field defined by u = x + 2y and v = 4 -y. In the domain where x and y vary from -10 to 10, where is there a stagnation point? Units for u and v are in meters/second, and x and y are in meters. Ox = 2 m. y = 1 m x = 2 m, y = 0 No stagnation point exists x = -8 m, y = 4 m Ox = 1 m, y = -1 m QUESTION 6 A one-dimensional flow through a nozzle has a velocity field of u = 3x + 2. What is the acceleration of a fluid particle through the nozzle? Assume u, x and the acceleration are all in consistent units. O 3 du/dt 9x + 6 1.5 x2 + 2x O Oarrow_forwardProblem (5.14): If u = ax and v = ay and w = -2az are the velocity components for a fluid flow in a particular case, check whether they satisfy the continuity equation. If they do, is the flow rotational or irrotational? Also obtain equation of streamline passing through the point (2, 2, 4) [Ans. Yes, irrotational x y, xz/2 = 41arrow_forwardAnswer question 3 in the attached image pleasearrow_forward
- The components of a two-dimensional velocity field are u = 4 + y³ and v = 16. The equation for a streamline can be written as y++ Ay + Bx + C = 0. Determine the values of the coefficients for the streamline passing through (3, 1). A = i B = i C= iarrow_forwardConsider a velocity field where the x and y components of velocity aregiven by u = cx and v = −cy, where c is a constant. Assuming the velocity field given is pertains to an incompressible flow, calculate the stream function and velocity potential.Using your results, show that lines of constant φ are perpendicular to linesof constant ψ.arrow_forwardConsider the velocity field represented by V = K (yĩ + xk) Rotation about z-axis isarrow_forward
- The velocity field for a fluid flow is given by following expression: =(0.2x² + 2y+2.5)î +(0.5x+2y² – 6) ĵ+(0.15x² + 3y° + z)k The strain tensor at (2,1,–1) will be: 0.8 1.25 0.30 a) | -1.25 -4 0.30 -1 (0.8 1.25 0.70 b) | 1.25 2 0.30 -2 1 0.8 1.25 0.30) c) | 1.25 4 -2 0.30 -2 1 0.8 1.25 0.30 d) | 1.25 8. -2 0.8 2 1arrow_forward6)arrow_forwardAn equation for the velocity for a 2D planar converging nozzle is Uy u =U1+ w=0 L Where U is the speed of the flow entering into the nozzle, and L is the length. Determine if these satisfy the continuity equation. Write the Navier-Stokes equations in x and y directions, simplify them appropriately, and integrate to determine the pressure distribution P(x.y) in the nozzle. Assume that at x = 0, y = 0, the pressure is a known value, P.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Introduction to Kinematics; Author: LearnChemE;https://www.youtube.com/watch?v=bV0XPz-mg2s;License: Standard youtube license