Fox And Mcdonald's Introduction To Fluid Mechanics
9th Edition
ISBN: 9781118921876
Author: Pritchard, Philip J.; Leylegian, John C.; Bhaskaran, Rajesh
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5, Problem 53P
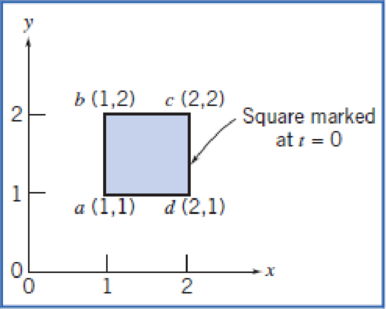
Consider the velocity field for flow in a rectangular “corner,”
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The flow field about a rotating cylinder with the radius a can be modelled by
superimposing the velocity potentials of a uniform flow filed, a doublet and a
potential vortex:
p = Ux[1+ (a/r)²] – (TO)/(2x)
Does this velocity potential satisfy the Laplace equation?
True
False
3.4 Consider a steady, incompressible, 2D velocity field for motion parallel to the
X-axis with constant shear. The shear rate is du/dy Ay. Obtain an expression for
the velocity field V. Calculate the rate of rotation. Evaluate the stream function
%3D
for this flow field.
Ay
Ay
+ В і, о,
Ay
+ By+ C
6.
Ans: V=
2
Velocity components in the flow of an ideal fluid in a horizontal plane; Given as u = 16 y - 12 x , v = 12 y - 9 x
a) Is the current continuous?(YES OR NO)
b) Can the potential function be defined?(YES OR NO)
c) Find the unit width flow passing between the origin and the point A(2,4). (y(0,0)=0)
d) Calculate the pressure difference between the origin and the point B(3;3).
Chapter 5 Solutions
Fox And Mcdonald's Introduction To Fluid Mechanics
Ch. 5 - Which of the following sets of equations represent...Ch. 5 - Which of the following sets of equations represent...Ch. 5 - In an incompressible three-dimensional flow field,...Ch. 5 - In a two-dimensional incompressible flow field,...Ch. 5 - The three components of velocity in a velocity...Ch. 5 - The x component of velocity in a steady,...Ch. 5 - The y component of velocity in a steady...Ch. 5 - The velocity components for an incompressible...Ch. 5 - The radial component of velocity in an...Ch. 5 - A crude approximation for the x component of...
Ch. 5 - A useful approximation for the x component of...Ch. 5 - A useful approximation for the x component of...Ch. 5 - For a flow in the xy plane, the x component of...Ch. 5 - Consider a water stream from a jet of an...Ch. 5 - Which of the following sets of equations represent...Ch. 5 - For an incompressible flow in the r plane, the r...Ch. 5 - A viscous liquid is sheared between two parallel...Ch. 5 - A velocity field in cylindrical coordinates is...Ch. 5 - Determine the family of stream functions that...Ch. 5 - The stream function for a certain incompressible...Ch. 5 - Determine the stream functions for the following...Ch. 5 - Determine the stream function for the steady...Ch. 5 - Prob. 23PCh. 5 - A parabolic velocity profile was used to model...Ch. 5 - A flow field is characterized by the stream...Ch. 5 - A flow field is characterized by the stream...Ch. 5 - Prob. 27PCh. 5 - A flow field is characterized by the stream...Ch. 5 - In a parallel one-dimensional flow in the positive...Ch. 5 - Consider the flow field given by V=xy2i13y3j+xyk....Ch. 5 - Prob. 31PCh. 5 - The velocity field within a laminar boundary layer...Ch. 5 - A velocity field is given by V=10ti10t3j. Show...Ch. 5 - The y component of velocity in a two-dimensional,...Ch. 5 - A 4 m diameter tank is filled with water and then...Ch. 5 - An incompressible liquid with negligible viscosity...Ch. 5 - Sketch the following flow fields and derive...Ch. 5 - Consider the low-speed flow of air between...Ch. 5 - As part of a pollution study, a model...Ch. 5 - As an aircraft flies through a cold front, an...Ch. 5 - Wave flow of an incompressible fluid into a solid...Ch. 5 - A steady, two-dimensional velocity field is given...Ch. 5 - A velocity field is represented by the expression...Ch. 5 - A parabolic approximate velocity profile was used...Ch. 5 - A cubic approximate velocity profile was used in...Ch. 5 - The velocity field for steady inviscid flow from...Ch. 5 - Consider the incompressible flow of a fluid...Ch. 5 - Consider the one-dimensional, incompressible flow...Ch. 5 - Expand (V)V in cylindrical coordinates by direct...Ch. 5 - Determine the velocity potential for (a) a flow...Ch. 5 - Determine whether the following flow fields are...Ch. 5 - The velocity profile for steady flow between...Ch. 5 - Consider the velocity field for flow in a...Ch. 5 - Consider the two-dimensional flow field in which u...Ch. 5 - Consider a flow field represented by the stream...Ch. 5 - Fluid passes through the set of thin, closely...Ch. 5 - A two-dimensional flow field is characterized as u...Ch. 5 - A flow field is represented by the stream function...Ch. 5 - Consider the flow field represented by the stream...Ch. 5 - Consider the flow field represented by the stream...Ch. 5 - Consider the velocity field given by V=Ax2i+Bxyj,...Ch. 5 - Consider again the viscometric flow of Example...Ch. 5 - The velocity field near the core of a tornado can...Ch. 5 - A velocity field is given by V=2i4xjm/s. Determine...Ch. 5 - Consider the pressure-driven flow between...Ch. 5 - Consider a steady, laminar, fully developed,...Ch. 5 - Assume the liquid film in Example 5.9 is not...Ch. 5 - Consider a steady, laminar, fully developed...Ch. 5 - Consider a steady, laminar, fully developed...Ch. 5 - A linear velocity profile was used to model flow...Ch. 5 - A cylinder of radius ri rotates at a speed ...Ch. 5 - The velocity profile for fully developed laminar...Ch. 5 - Assume the liquid film in Example 5.9 is...Ch. 5 - The common thermal polymerase chain reaction (PCR)...Ch. 5 - A tank contains water (20C) at an initial depth y0...Ch. 5 - For a small spherical particle of styrofoam...Ch. 5 - Use Excel to generate the progression to an...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- X=1 X=7 2. A fluid flow is described by the velocity vector; U = 5x³i - 15x²yj (a) Determine the shear strain rate. (b) Find the stream function of the flow. (c) Find the velocity potential of the flow.arrow_forward1. For a certain incompressible two-dimensional flow, the stream function, ψ(x, y) is prescribed. Is the continuity equation satisfied? 2. If u = −Ae−ky cos kx and v = −Ae−ky sin kx, find the stream function. Is this flow rotational, or irrotational?arrow_forwardRequired information A simple flow model for a two-dimensional converging nozzle is the distribution u = U₁(1+z) v = − U₁7/10 w = 0. Find the pressure distribution p(x, y) when the pressure at the origin equals po. Neglect gravity. Multiple Choice p= Po -² (2 + + 7) + P p=-2/²2 (2-) + Po p PU =_/²2(x + 1 + 1) + P. 3L Karrow_forward
- Problem 1 Given a steady flow, where the velocity is described by: u = 3 cos(x) + 2ry v = 3 sin(y) + 2?y !! !! a) Find the stream function if it exists. b) Find the potential function if it exists. c) For a square with opposite diagonal corners at (0,0) and (47, 27), evaluate the circu- lation I = - f V.ds where c is a closed path around the square. d) Calculate the substantial derivative of velocity at the center of the same box.arrow_forward6)arrow_forwardQ.5 The velocity components in x and y direction 2 are given by u = Axy° - xy; v = > ху; v — ху = xy² – 3/4 .4 y*. The value of A for a possible flow field involving an incompressible fluid is: A -3/4 В 3 C 4/3 D -4/3arrow_forward
- Consider a velocity field where the x and y components of velocity aregiven by u = cy/(x2 + y2) and v = −cx/(x2 + y2), where c is a constant. For vortex flow, calculate: a. The time rate of change of the volume of a fluid element per unitvolume.b. The vorticity.arrow_forward1. For a velocity field described by V = 2x2i − zyk, is the flow two- or threedimensional? Incompressible? 2. For an Eulerian flow field described by u = 2xyt, v = y3x/3, w = 0, find the slope of the streamline passing through the point [2, 4] at t = 2. 3. Find the angle the streamline makes with the x-axis at the point [-1, 0.5] for the velocity field described by V = −xyi + 2y2jarrow_forwardThe velocity components for idealised flow along a right angled wall is given by u = 4 x m/s, v = -4 y m/s, w = 0 m/s. Find the vorticity magnitude at position x=(1,2,1) cm. Give your answer to two decimal places.arrow_forward
- Consider the flow field V = (ay+dx)i + (bx-dy)j + ck, where a(t), b(t), c(t), and d(t) are time dependent coefficients. Prove the density is constant following a fluid particle, then find the pressure gradient vector gradP, Γ for a circular contour of radius R in the x-y plane (centered on the origin) using a contour integral, and Γ by evaluating the Stokes theorem surface integral on the hemisphere of radius R above the x-y plane bounded by the contour.arrow_forwardProblem 6: Consider the incompressible Newtonian pipe flow (Fig. 6). Assume the flow is essentially axial, vz + 0 but v = ve = 0 and ôlƏe = 0. The flow is fully developed and steady in a horizontal pipe with the constant pressure gradient. Apply the Navier-Stokes equations and: a) Develop simplified governing equations (continuity and momentum) for this flow; b) Apply the boundary conditions and determine the velocity profile; and c) Develop expressions for the flow rate and mean velocity from the velocity profile. Vz Fig. 6 Flow in circular pipe 1.1 GB used DELL F5 F6 F7 F8 211arrow_forward2. Consider a stream function given by = (²+x²). (a) Does this flow satisfy conservation of mass? Show your work. (b) Plot the streamlines for this flow. Let K= 2. Be sure to indicate the direction of the flow. (c) Is this flow irrotational? If so, find the velocity potential for this flow. If not, show that a velocity potential does not exist. (d) Describe the flow represented by this stream function.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Introduction to Kinematics; Author: LearnChemE;https://www.youtube.com/watch?v=bV0XPz-mg2s;License: Standard youtube license