Fox And Mcdonald's Introduction To Fluid Mechanics
9th Edition
ISBN: 9781118921876
Author: Pritchard, Philip J.; Leylegian, John C.; Bhaskaran, Rajesh
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5, Problem 47P
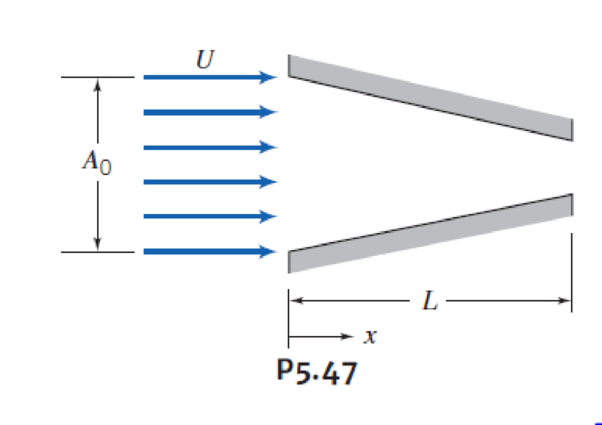
Consider the incompressible flow of a fluid through a nozzle as shown. The area of the nozzle is given by A = A0(l − bx) and the inlet velocity varies according to U = U0(0.5 + 0.5cos ωt) where A0 = 5 ft2, L = 20 ft, b = 0.02 ft-1, ω = 0.16 rad/s and U0 = 20ft/s. Find and plot the acceleration on the centerline, with time as a parameter.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Velocity Profiles for Flow Between Parallel Plates. In Example 8.3-2, a fluid is flowing between vertical parallel plates with one plate moving. Do as follows:
1. Determine the average velocity and the maximum velocity.
2. Make a sketch of the velocity profile for three cases where the surface is moving upward, moving downward, and stationary.
Methane in the gaseous state flows at a rate of 0.072 m^3/s in a pipe at a
temperature of 27°C and gauge pressure of 148.675kPa (point 1). The pipe is
divided into two branches (point 2 and 3), as seen in the figure. If the exit
velocity in pipe 3 is 12 m/s with a density of 1.9 kg/m^3, what is the flow rate and
velocity in pipe 2? Consider that in section 2 the fluid is leaving with a
temperature of 402°C and an absolute pressure of 175 kPa. We have an
atmospheric pressure of 101.325 kPa and R_methane = 0.5182 kJ/kg ⚫K.
(1)
Inflow
D1
D3=50mm
D2=100mm
(3)
(2)
Assume the temperature of the exhaust in an exhaust pipe can be approximated by
T = To (1 + ae-bx) [1 + c cos(@t)],
where To = 100 °C, a = 3, b = 0.03 m ¹, c = 0.066, and w = 100 rad/s. If the exhaust speed is a constant 3 m/s, determine the time rate of
change of temperature of the fluid particles at (a) x = 0 and (b) x = 4 m when t = 0.
DT
(a)
°C/s
(b)
Dt
DT
Dt
=
°C/s
Chapter 5 Solutions
Fox And Mcdonald's Introduction To Fluid Mechanics
Ch. 5 - Which of the following sets of equations represent...Ch. 5 - Which of the following sets of equations represent...Ch. 5 - In an incompressible three-dimensional flow field,...Ch. 5 - In a two-dimensional incompressible flow field,...Ch. 5 - The three components of velocity in a velocity...Ch. 5 - The x component of velocity in a steady,...Ch. 5 - The y component of velocity in a steady...Ch. 5 - The velocity components for an incompressible...Ch. 5 - The radial component of velocity in an...Ch. 5 - A crude approximation for the x component of...
Ch. 5 - A useful approximation for the x component of...Ch. 5 - A useful approximation for the x component of...Ch. 5 - For a flow in the xy plane, the x component of...Ch. 5 - Consider a water stream from a jet of an...Ch. 5 - Which of the following sets of equations represent...Ch. 5 - For an incompressible flow in the r plane, the r...Ch. 5 - A viscous liquid is sheared between two parallel...Ch. 5 - A velocity field in cylindrical coordinates is...Ch. 5 - Determine the family of stream functions that...Ch. 5 - The stream function for a certain incompressible...Ch. 5 - Determine the stream functions for the following...Ch. 5 - Determine the stream function for the steady...Ch. 5 - Prob. 23PCh. 5 - A parabolic velocity profile was used to model...Ch. 5 - A flow field is characterized by the stream...Ch. 5 - A flow field is characterized by the stream...Ch. 5 - Prob. 27PCh. 5 - A flow field is characterized by the stream...Ch. 5 - In a parallel one-dimensional flow in the positive...Ch. 5 - Consider the flow field given by V=xy2i13y3j+xyk....Ch. 5 - Prob. 31PCh. 5 - The velocity field within a laminar boundary layer...Ch. 5 - A velocity field is given by V=10ti10t3j. Show...Ch. 5 - The y component of velocity in a two-dimensional,...Ch. 5 - A 4 m diameter tank is filled with water and then...Ch. 5 - An incompressible liquid with negligible viscosity...Ch. 5 - Sketch the following flow fields and derive...Ch. 5 - Consider the low-speed flow of air between...Ch. 5 - As part of a pollution study, a model...Ch. 5 - As an aircraft flies through a cold front, an...Ch. 5 - Wave flow of an incompressible fluid into a solid...Ch. 5 - A steady, two-dimensional velocity field is given...Ch. 5 - A velocity field is represented by the expression...Ch. 5 - A parabolic approximate velocity profile was used...Ch. 5 - A cubic approximate velocity profile was used in...Ch. 5 - The velocity field for steady inviscid flow from...Ch. 5 - Consider the incompressible flow of a fluid...Ch. 5 - Consider the one-dimensional, incompressible flow...Ch. 5 - Expand (V)V in cylindrical coordinates by direct...Ch. 5 - Determine the velocity potential for (a) a flow...Ch. 5 - Determine whether the following flow fields are...Ch. 5 - The velocity profile for steady flow between...Ch. 5 - Consider the velocity field for flow in a...Ch. 5 - Consider the two-dimensional flow field in which u...Ch. 5 - Consider a flow field represented by the stream...Ch. 5 - Fluid passes through the set of thin, closely...Ch. 5 - A two-dimensional flow field is characterized as u...Ch. 5 - A flow field is represented by the stream function...Ch. 5 - Consider the flow field represented by the stream...Ch. 5 - Consider the flow field represented by the stream...Ch. 5 - Consider the velocity field given by V=Ax2i+Bxyj,...Ch. 5 - Consider again the viscometric flow of Example...Ch. 5 - The velocity field near the core of a tornado can...Ch. 5 - A velocity field is given by V=2i4xjm/s. Determine...Ch. 5 - Consider the pressure-driven flow between...Ch. 5 - Consider a steady, laminar, fully developed,...Ch. 5 - Assume the liquid film in Example 5.9 is not...Ch. 5 - Consider a steady, laminar, fully developed...Ch. 5 - Consider a steady, laminar, fully developed...Ch. 5 - A linear velocity profile was used to model flow...Ch. 5 - A cylinder of radius ri rotates at a speed ...Ch. 5 - The velocity profile for fully developed laminar...Ch. 5 - Assume the liquid film in Example 5.9 is...Ch. 5 - The common thermal polymerase chain reaction (PCR)...Ch. 5 - A tank contains water (20C) at an initial depth y0...Ch. 5 - For a small spherical particle of styrofoam...Ch. 5 - Use Excel to generate the progression to an...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
?.1 Define the different reference meridians that can be used for the direction ofa line.
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Write an accessor method called getPrecision that can be added to the class Calculator in Listing 9.12 and that...
Java: An Introduction to Problem Solving and Programming (8th Edition)
Comprehension Check 8-15
You push an automobile with a constant force of 20 pound-force [lbf] until 1,500 joule...
Thinking Like an Engineer: An Active Learning Approach (4th Edition)
(Temperature Conversions) Implement the following integer methods: Method celsius returns the Celsius equivalen...
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
Create an application that converts Celsius to Fahrenheit. The formula is F = 1.8 C + 32 where F is the Fahren...
Starting Out With Visual Basic (8th Edition)
What does array bounds checking mean?
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Air at 30C and atmospheric pressure flows with a velocity of 6.5 m/s through a 7.5 cmdiameter pipe shown in Figure Q 1(a). The average wall roughness of the pipe is 0.002mmand the value of μ/ρ is 1.6x10-5 m2/s at 30C. Where μ is the coefficient of dynamic viscosityof air and ρ is the density of air. Determine the friction head loss across 30m length of thepipe.arrow_forwardAn incompressible fluid flows in the converging pipe.A=Ao*(1-b*x) is given for pipe area.Input speed is V=Vo*(0,5+0,5*cos*ω*t).Given as Ao=1,5 m2, L=13m, b=0,2/15 , ω =0,16rad/s. , Vo=3 m/sFind the acceleration in the center of pipe as a function of time (t).arrow_forwardWater steam is running through the nozzle. Inlet pressure is P1=25 bars; T1=300C; V1=90m/s; A1=0.2m2. The exit parameters are: P2=11bars; T2=210C. The mass flow rate is m=2 kg/s. Determine: a.Exit velocity V2=?; b.Inlet and outlet diameters D1 and D2. show all stepsarrow_forward
- Please help me with this fluid mechanics question! Thank you!! :) A 1967 Harley-Davidson Shovelhead motorcycle uses a ventruri-carburetor to mix air and fuel for combustion. The venturi reduces the pressure to draw fuel from a reservoir chamber and to mix with the airstream as shown in the figure. The energy loss of the metering line is given by hL= (K*V^2)/2where K = 6.0 and V is the fuel velocity in the metering line. Assume that the air is an ideal fluid (68°F). Calculate the mass flux of air and the mass flux of fuel. Hint: Assume the air intake velocity is negligible.arrow_forwardA brand of toothpaste is made using a mixture of white and red paste. During the manufacturing process, both pastes are pumped through a pipe, with the red paste lying in the center of the pipe, as shown in Figure Q2. The pipe has an internal radius, R2, and the segment of red paste has a radius R1. The flow is found to follow the Poiseuille equation, i.e. 1 dp u(r) = -- 4µdx (R²2-²) Where u is the viscosity of the paste and dp dx is the pressure gradient. The total flow of toothpaste through the pipe is Qtot, and the flowrate of the red paste is Qred. The toothpaste has a density of p = 1200 kg/m3, and a viscosity of 0.03 Pa.s. The pipe has a radius R2 = 5 cm and a length L = 2 m. a) Find an expression for the flowrate of the red toothpaste. You answer should be in terms of µ, R1, R2, dp dx) b) The flow in the pipe becomes turbulent when the Reynolds number reaches 2000 (where Re is calculated using the mean velocity across the pipe). What is the maximum pressure drop along the pipe…arrow_forwardThe velocity profile of a liquid flows through the z direction of the vertical tube (figure right) with the radius ro is given as; r 1 dp Vz = (r² – r3) 2µ dz Specify the maximum velocity and derive an expression for the average velocity.arrow_forward
- Continuity equation: Calculate the inside diameter of the pipes at the inlet and outleta hydraulic pump whose volume flow is 40 l/min, knowing that the oil enters the pump at a speed of 1.2 m/sec andexits at a maximum speed of 3.5 m/sec. Answer: D1 = 26.6 mm and D2 = 15.6 mmarrow_forwardWater steam is running through the nozzle. Inlet pressure is P1=25 bars; T1=300C; V1=90m/s; A1=0.2m2. The exit parameters are: P2=11bars; T2=210C. The mass flow rate is m=2 kg/s. Determine: a.Exit velocity V2=?; b.Inlet and outlet diameters D1 and D2.arrow_forwardPlease Answer Both!!!arrow_forward
- What must the gauge pressure p be at A if the volume flow rate out of the pipe at point B is 0.0800 m^3/s?arrow_forwardplease refer to image tqarrow_forwardWater flows in a 170 mm diameter pipeline (A) divides into two smaller pipelines, one being 100 mm in diameter (D) and the other being 80 mm in diameter (B). If the velocity in the 80 mm pipe (B) is 0.6m/s and that in the 100 mm pipe (D) is 0.9m/s, calculate the velocity in m/s and the mass flow rate in kg/s in the 170 mm pipe (A.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Physics 33 - Fluid Statics (1 of 10) Pressure in a Fluid; Author: Michel van Biezen;https://www.youtube.com/watch?v=mzjlAla3H1Q;License: Standard YouTube License, CC-BY