Chapter 5, Problem 44P

For the problem specified in the table, build upon the results of the original problem to determine the minimum factor of safety for yielding. Use both the maximum-shear-stress theory and the distortion-energy theory, and compare the results. The material is 1018 CD steel.

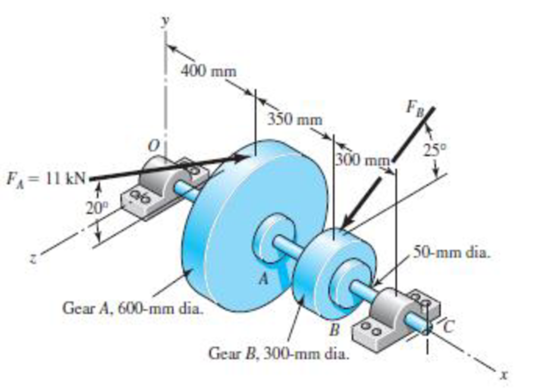
3–72* to 3–73*    A gear reduction unit uses the countershaft shown in the figure. Gear A receives power from another gear with the transmitted force F_A applied at the 20° pressure angle as shown. The power is transmitted through the shaft and delivered through gear B through a transmitted force F_B at the pressure angle shown.

(a)    Determine the force F_B, assuming the shaft is running at a constant speed.

(b)    Find the bearing reaction forces, assuming the bearings act as simple supports.

(c)    Draw shear-force and bending-moment diagrams for the shaft. If needed, make one set for the horizontal plane and another set for the vertical plane.

(d)    At the point of maximum bending moment, determine the bending stress and the torsional shear stress.

(e)    At the point of maximum bending moment, determine the principal stresses and the maximum shear stress.

To determine

The factor of safety for yielding from maximum-shear-stress theory.

The factor of safety for yielding from distortion-energy theory.

Answer to Problem 44P

The factor of safety for yielding from maximum-shear-stress theory is $0.88$.

The factor of safety for yielding from distortion-energy theory is $0.93$.

Explanation of Solution

The figure below shows the free body diagram of pulley A.

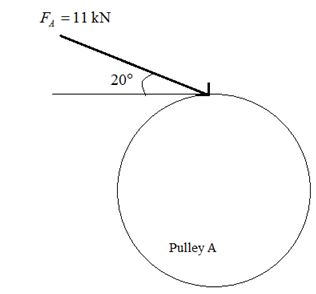
Figure-(1)

The figure below shows the free body diagram of pulley B.

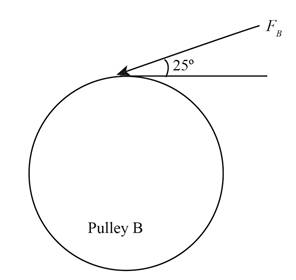
Figure-(2)

Calculate the force $F_B$, using the net torque equation.

    $\begin{array}{l}{\displaystyle \sum T}=0\\ -\left(F_A\times \frac{d_A}{2}\times \cos {\theta }_1\right)+\left(F_B\times \frac{d_B}{2}\times \cos {\theta }_2\right)=0\\ F_B=F_A\frac{d_A\cos {\theta }_1}{d_B\cos {\theta }_2}\end{array}$                                                  (I)

Here, the force acting on pulley $A$ is $F_A$, the diameter of pulley $A$ is $d_A$, the angle at which force acts on pulley $A$ is ${\theta }_1$, the force acting on pulley $B$ is $F_B$, the diameter of pulley $B$ is $d_B$ and the angle at which force acts on pulley $B$ is ${\theta }_2$.

Write the moment about bearing $O$ in $z\text{-}$ direction.

  $\begin{array}{l}{\displaystyle \sum M_{Oz}}=0\\ \left[\begin{array}{l}-\left(F_A\sin {\theta }_1\times l_{OA}\right)\\ -\left(F_B\sin {\theta }_2\times \left(l_{OA}+l_{AB}\right)\right)\\ +R_{Cy}\times \left(l_{OA}+l_{AB}+l_{BC}\right)\end{array}\right]=0\\ R_{Cy}=\frac{\left[\begin{array}{l}\left(F_B\sin {\theta }_2\times \left(l_{OA}+l_{AB}\right)\right)\\ +\left(F_A\sin {\theta }_1\times l_{OA}\right)\end{array}\right]}{\left(l_{OA}+l_{AB}+l_{BC}\right)}\end{array}$                                                                     (II)

Here, the reaction force at bearing $C$ in $y\text{-}$ direction is $R_{Cy}$, the distance between $O$ and $A$ is $l_{OA}$, the distance between $A$ and $B$ is $l_{AB}$ and the distance between $B$ and $C$ is $l_{BC}$.

Write the equation to balance the forces in $y\text{-}$ direction.

    $\begin{array}{l}{\displaystyle \sum F_y}=0\\ R_{Oy}-F_A\sin {\theta }_1+R_{Cy}-F_B\sin {\theta }_2=0\\ R_{Oy}=F_B\sin {\theta }_2-R_{Cy}+F_A\sin {\theta }_1\end{array}$                                                              (III)

Here, the reaction force at bearing $O$ in $y\text{-}$ direction is $R_{Oy}$.

Write the moment about bearing $O$ in $y\text{-}$ direction.

  $\begin{array}{l}{\displaystyle \sum M_{Oy}}=0\\ \left[\begin{array}{l}\left(F_A\cos {\theta }_1\times l_{OA}\right)\\ -\left(F_B\cos {\theta }_2\times \left(l_{OA}+l_{AB}\right)\right)\\ -R_{Cz}\times \left(l_{OA}+l_{AB}+l_{BC}\right)\end{array}\right]=0\\ R_{Cz}=\frac{\left[\begin{array}{l}\left(F_A\cos {\theta }_1\times l_{OA}\right)\\ -\left(F_B\cos {\theta }_2\times \left(l_{OA}+l_{AB}\right)\right)\end{array}\right]}{\left(l_{OA}+l_{AB}+l_{BC}\right)}\end{array}$                                                               (IV)

Here, the reaction force at bearing $C$ in $z\text{-}$ direction is $R_{Cz}$.

Write the equation to balance the forces in $z\text{-}$ direction.

    $\begin{array}{l}{\displaystyle \sum F_z}=0\\ R_{Oz}-F_A\cos {\theta }_1+R_{Cz}+F_B\cos {\theta }_2=0\\ R_{Oz}=F_A\cos {\theta }_1-R_{Cz}+F_B\cos {\theta }_2\end{array}$                                                             (V)

Here, the reaction force at bearing $O$ in $z\text{-}$ direction is $R_{Oz}$.

Calculate the reaction forces at bearing $O$.

    $R_O=\sqrt{R_{Oy}^2+R_{Oz}^2}$                                                                                       (VI)

Here, the reaction force at bearing $O$ is $R_O$.

Calculate the reaction forces at bearing $C$.

    $R_C=\sqrt{R_{Cy}^2+R_{Cz}^2}$                                                                                      (VII)

Here, the reaction force at bearing $C$ is $R_C$.

The calculations for shear force and bending moment diagram in $y\text{-}$ direction.

Calculate the shear force at $O$ in $y\text{-}$ direction.

    $S{F}_{Oy}=R_{Oy}$                                                                                               (VIII)

Here, the shear force at $O$ in $y\text{-}$ direction is $S{F}_{Oy}$.

Calculate the shear force at $A$ in $y\text{-}$ direction.

    $S{F}_{Ay}=S{F}_{Oy}-F_A\sin {\theta }_1$                                                                              (IX)

Here, the shear force at $A$ in $y\text{-}$ direction is $S{F}_{Ay}$.

Calculate the shear force at $B$ in $y\text{-}$ direction.

    $S{F}_{By}=S{F}_{Ay}-\left(F_B\sin {\theta }_2\right)$                                                                            (X)

Here, the shear force at $B$ in $y\text{-}$ direction is $S{F}_{By}$.

Calculate the shear force at $C$ in $y\text{-}$ direction.

    $S{F}_{Cy}=S{F}_{By}+R_{Cy}$                                                                          (XI)

Here, the shear force at $B$ in $y\text{-}$ direction is $S{F}_{By}$.

Calculate the moment at $O$ and $C$.

    $M_O=M_C=0$                                                                                     (XII)

Here, the moment at $O$ is $M_O$ and the moment at $C$ is $M_C$.

Calculate the moment at $A$ in $y\text{-}$ direction.

    $M_{Ay}=S{F}_{Oy}\times l_{OA}$                                                                                 (XIII)

Here, the moment at $A$ in $y\text{-}$ direction is $M_{Ay}$.

Calculate the moment at $B$ in $y\text{-}$ direction.

    $M_{By}=F_B\sin {\theta }_2\times l_{CB}$                                                                        (XIV)

Here, the moment at $B$ in $y\text{-}$ direction is $M_{By}$.

The calculations for shear force and bending moment diagram in $z\text{-}$ direction.

Calculate the shear force at $O$ in $y\text{-}$ direction.

    $S{F}_{Oz}=-R_{Oz}$                                                                                              (XV)

Here, the shear force at $O$ in $z\text{-}$ direction is $S{F}_{Oz}$.

Calculate the shear force at $A$ in $z\text{-}$ direction.

    $S{F}_{Az}=S{F}_{Oz}+F_A\cos {\theta }_1$                                                                            (XVI)

Here, the shear force at $A$ in $z\text{-}$ direction is $S{F}_{Az}$.

Calculate the shear force at $B$ in $z\text{-}$ direction.

    $S{F}_{Bz}=S{F}_{Az}-F_B\cos {\theta }_2$                                                                           (XVII)

Here, the shear force at $B$ in $z\text{-}$ direction is $S{F}_{Bz}$.

Calculate the shear force at $C$ in $z\text{-}$ direction.

    $S{F}_{Cz}=S{F}_{Bz}-R_{Cz}$                                                                        (XVIII)

Here, the shear force at $C$ in $z\text{-}$ direction is $S{F}_{Cz}$.

Calculate the moment at $O$ and $C$.

    $M_O=M_C=0$                                                                                     (XIX)

Here, the moment at $O$ is $M_O$ and the moment at $C$ is $M_C$.

Calculate the moment at $A$ in $z\text{-}$ direction.

    $M_{Az}=S{F}_{Az}\times l_{OA}$                                                                                (XX)

Here, the moment at $A$ in $z\text{-}$ direction is $M_{Az}$.

Calculate the moment at $B$ in $z\text{-}$ direction.

    $M_{Bz}=R_{Cz}\times l_{BC}$                                                                        (XXI)

Here, the moment at $B$ in $z\text{-}$ direction is $M_{Bz}$.

Write the net moment at $A$.

    $M_A=\sqrt{M_{Ay}^2+M_{Az}^2}$                                                                      (XXII)

Here, the net moment at $A$ is $M_A$.

Write the net moment at $B$.

    $M_B=\sqrt{M_{By}^2+M_{Bz}^2}$                                                                      (XXIII)

Here, the net moment at $C$ is $M_C$.

Write the torque transmitted by shaft from $A$ to $B$.

    $T=F_A\cos {\theta }_1\times \frac{d_A}{2}$                                                                        (XXIV)

Here, the torque transmitted by shaft from $A$ to $B$ is $T$.

Calculate the bending stress.

    $\sigma =\frac{32M_B}{\pi d^3}$                                                                                     (XXV)

Here, the bending stress is $\sigma$ and diameter of shaft is $d$.

Calculate the shear stress.

    $\tau =\frac{16T}{\pi d^3}$                                                                                           (XVI)

Here, the shear stress is $\tau$.

Calculate the maximum principal stress.

    ${\sigma }_1=\frac{\sigma }{2}+\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$                                                                   (XXVII)

Here, the maximum principal stress is ${\sigma }_1$.

Calculate the minimum principal stress.

    ${\sigma }_2=\frac{\sigma }{2}-\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$                                                                   (XXVIII)

Here, the minimum principal stress is ${\sigma }_2$.

Calculate the maximum shear stress.

    ${\tau }_{\max }=\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$                                                                           (XXIX)

Here, maximum shear stress is ${\tau }_{\max }$.

Calculate the factor of safety from maximum-shear-stress theory.

    $n=\frac{S_y}{{\sigma }_1-{\sigma }_2}$                                                                                            (XXX)

Here, the maximum yield stress for $1018$ CD steel is $S_y$.

Calculate the factor of safety from distortion-energy theory.

    $n=\frac{S_y}{\sigma \text{'}}$                                                                                              (XXXI)

Here, the Von Mises stress is $\sigma \text{'}$.

Write the expression for von Mises stress.

    $\sigma \text{'}={\left({\sigma }_1^2-{\sigma }_1.{\sigma }_2+{\sigma }_2^2\right)}^{\frac{1}{2}}$

Substitute $\left[{\left({\sigma }_1^2-{\sigma }_1.{\sigma }_2+{\sigma }_2^2\right)}^{\frac{1}{2}}\right]$ for $\sigma \text{'}$ in Equation (XXXI).

    $n=\frac{S_y}{\left[{\left({\sigma }_1^2-{\sigma }_1.{\sigma }_2+{\sigma }_2^2\right)}^{\frac{1}{2}}\right]}$                                                               (XXXII)

Conclusion:

Convert the forces into $\text{N}$.

    $\begin{array}{c}{F}_A=11\text{kN}\times \frac{1000\text{N}}{1\text{kN}}\\ =11000\text{N}\end{array}$

Substitute $11000\text{N}$ for $F_A$, $600\text{mm}$ for $d_A$, $20°$ for ${\theta }_1$, $300\text{mm}$ for $d_B$ and $25°$ for ${\theta }_2$ in Equation (I).

    $\begin{array}{c}{F}_B=11000\text{N}\times \frac{600\text{mm}\times \cos 20°}{300\text{mm}\times \cos 25°}\\ =22810.3\text{N}\\ \approx 22810\text{N}\end{array}$

Substitute $22810\text{N}$ for $F_B$, $20°$ for ${\theta }_1$, $11000\text{N}$ for $F_A$, $25°$ for ${\theta }_2$, $400\text{mm}$ for $l_{OA}$, $350\text{mm}$ for $l_{AB}$ and $300\text{mm}$ for $l_{BC}$ in Equation (II).

    $\begin{array}{c}{R}_{Cy}=\frac{\left[\left(22810\text{N}\times \sin 25°\times \left(400\text{mm}+350\text{mm}\right)\right)+\left(11000\text{N}\times \sin 20°\times 400\text{mm}\right)\right]}{\left(400\text{mm}+350\text{mm}+300\text{mm}\right)}\\ =\frac{\left[\left(22810\text{N}\times \sin 25°\times \left(450\text{mm}\right)\right)+\left(11000\text{N}\times \sin 20°\times 400\text{mm}\right)\right]}{\left(1050\text{mm}\right)}\\ =8318.88\text{N}\\ \approx 8319\text{N}\end{array}$

Substitute $22810\text{N}$ for $F_B$, $25°$ for ${\theta }_2$, $8319\text{N}$ for $R_{Cy}$, $11000\text{N}$ for $F_A$ and $20°$ for ${\theta }_1$ in Equation (III).

    $\begin{array}{c}{R}_{Oy}=\left(22810\text{N}\times \sin 25°\right)-\left(8319\text{N}\right)+\left(11000\text{N}\times \sin 20°\right)\\ =5083.1\text{N}\\ \approx 5083\text{N}\end{array}$

Substitute $22810\text{N}$ for $F_B$, $20°$ for ${\theta }_1$, $11000\text{N}$ for $F_A$, $25°$ for ${\theta }_2$, $400\text{mm}$ for $l_{OA}$, $350\text{mm}$ for $l_{AB}$ and $300\text{mm}$ for $l_{BC}$ in Equation (IV).

    $\begin{array}{c}{R}_{Cz}=\frac{\left[\left(11000\text{N}\times \cos 20°\times 400\text{mm}\right)-\left(22810\text{N}\times \cos 25°\times \left(400\text{mm}+350\text{mm}\right)\right)\right]}{\left(400\text{mm}+350\text{mm}+300\text{mm}\right)}\\ =\frac{\left[\left(11000\text{N}\times \cos 20°\times 400\text{mm}\right)-\left(22810\text{N}\times \cos 25°\times 750\text{mm}\right)\right]}{\left(1050\text{mm}\right)}\\ =-10830\text{N}\end{array}$

Substitute $11000\text{N}$ for $F_A$, $20°$ for ${\theta }_1$, $-10830\text{N}$ for $R_{Cz}$, $22810\text{N}$ for $F_B$ and $25°$ for ${\theta }_2$ in Equation (V).

    $\begin{array}{c}{R}_{Oz}=\left(11000\text{N}\cos 20°\right)+10830\text{N}-\left(22810\text{N}\times \cos 25°\right)\\ =493.7\text{N}\\ \approx 494\text{N}\end{array}$

Substitute $5.083\text{kN}$ for $R_{Oy}$ and $0.494\text{kN}$ for $R_{Oz}$ in Equation (VI).

    $\begin{array}{c}{R}_O=\sqrt{{\left(5083\text{N}\right)}^2+{\left(494\text{N}\right)}^2}\\ =5106.9\text{N}\\ =5107\text{N}\end{array}$

Substitute $8.319\text{kN}$ for $R_{Cy}$ and $-10.83\text{kN}$ for $R_{Cz}$ in Equation (VII).

    $\begin{array}{c}{R}_C=\sqrt{{\left(8319\text{N}\right)}^2+{\left(-10830\text{N}\right)}^2}\\ =13656.3\text{N}\\ \approx 13656\text{N}\end{array}$

Substitute $5083\text{N}$ for $R_{Oy}$ in Equation (VIII).

    $S{F}_{Oy}=5083\text{N}$

Substitute $5083\text{N}$ for $S{F}_{Oy}$, $11000\text{N}$ for $F_A$ and $20°$ for ${\theta }_1$ in Equation (IX.)

    $\begin{array}{c}S{F}_{Ay}=5083\text{N}-\left(11000\text{N}\times \sin 20\right)\\ =1320.7\text{N}\\ \approx 1321\text{N}\end{array}$

Substitute $1321\text{N}$ for $S{F}_{Ay}$, $22810\text{N}$ for $F_B$ and $25°$ for ${\theta }_2$ in Equation (X).

    $\begin{array}{c}S{F}_{By}=1321\text{N}-\left(22810\text{N}\times \sin 25\right)\\ =-8318.92\text{N}\\ \simeq -8319\text{N}\end{array}$

Substitute $-8319\text{N}$ for $S{F}_{By}$ and $8319\text{N}$ for $R_{Cy}$ in Equation (XI).

    $\begin{array}{c}S{F}_{Cy}=-8319\text{N}+8319\text{N}\\ =0\text{N}\end{array}$

Substitute $5083\text{N}$ for $S{F}_{Oy}$ and $400\text{mm}$ for $l_{OA}$ in Equation (XIII).

    $\begin{array}{c}{M}_{Ay}=5083\text{N}\times 400\text{mm}\times \frac{1\text{m}}{1000\text{mm}}\\ =2033.2\text{N}\cdot \text{m}\\ \approx 2033\text{N}\cdot \text{m}\end{array}$

Substitute $22810\text{N}$ for $F_B$, $25°$ for ${\theta }_2$ and $300\text{mm}$ for $l_{BC}$ in Equation (XIV).

    $\begin{array}{c}{M}_{By}=22810\text{N}\times \sin 25°\times 300\text{m}\times \frac{1\text{m}}{1000\text{mm}}\\ =2496\text{N}\cdot \text{m}\end{array}$

Substitute $494\text{N}$ for $R_{Oz}$ in Equation (XV).

    $S{F}_{Oz}=-494\text{N}$

Substitute $-494\text{N}$ for $S{F}_{Oz}$, $11000\text{N}$ for $F_A$ and $20°$ for ${\theta }_1$ in Equation (XVI).

    $\begin{array}{c}S{F}_{Az}=-494\text{N}+\left(11000\text{N}\times \cos 20°\right)\\ =9843\text{N}\end{array}$

Substitute $9843\text{N}$ for $S{F}_{Az}$, $22810\text{N}$ for $F_B$ and $25°$ for ${\theta }_2$ in Equation (XVII).

    $\begin{array}{c}S{F}_{Bz}=9843\text{N}-\left(22810\text{N}\times \cos 25°\right)\\ =-10830\text{N}\end{array}$

Substitute $-10830\text{N}$ for $S{F}_{Bz}$ and $-10830\text{N}$ for $R_{Cz}$ in Equation (XVIII).

    $\begin{array}{c}S{F}_{Cz}=-10830\text{N}-\left(-10830\text{N}\right)\\ =0\text{N}\end{array}$

Substitute $-494\text{N}$ for $S{F}_{Oy}$ and $400\text{mm}$ for $l_{OA}$ in Equation (XX).

    $\begin{array}{c}{M}_{Az}=-494\text{N}\times 400\text{mm}\times \frac{1\text{m}}{1000\text{mm}}\\ =-198\text{N}\cdot \text{m}\end{array}$

Substitute $10830\text{N}$ for $F_B$ and $300\text{mm}$ for $l_{BC}$ in Equation (XXI).

    $\begin{array}{c}{M}_{Bz}=10830\text{N}\times 300\text{mm}\times \frac{1\text{m}}{1000\text{mm}}\\ =3249\text{N}\cdot \text{m}\end{array}$

Substitute $2033\text{N}\cdot \text{m}$ for $M_{Ay}$ and $-198\text{N}\cdot \text{m}$ for $M_{Az}$ in Equation (XXII).

    $\begin{array}{c}{M}_A=\sqrt{{\left(2033\text{N}\cdot \text{m}\right)}^2+{\left(-198\text{N}\cdot \text{m}\right)}^2}\\ =2042.6\text{N}\cdot \text{m}\\ \approx 2043\text{N}\cdot \text{m}\end{array}$

Substitute $2496\text{N}\cdot \text{m}$ for $M_{By}$ and $3249\text{N}\cdot \text{m}$ for $M_{Bz}$ in Equation (XXIII).

    $\begin{array}{c}{M}_B=\sqrt{{\left(2496\text{N}\cdot \text{m}\right)}^2+{\left(3249\text{N}\cdot \text{m}\right)}^2}\\ =4097\text{N}\cdot \text{m}\end{array}$

Since, $M_B>M_A$.

The critical location is at $B$.

Substitute $11000\text{N}$ for $F_A$, $20°$ for ${\theta }_1$ and $600\text{mm}$ for $d_A$ in Equation (XXIV).

    $\begin{array}{c}T=11000\text{N}\times \cos 20°\times \frac{\left(600\text{mm}\times \frac{1\text{m}}{1000\text{mm}}\right)}{2}\\ =3100.98\text{N}\cdot \text{m}\\ \approx 3101\text{N}\cdot \text{m}\end{array}$

Substitute $4097\text{N}\cdot \text{m}$ for $M_B$ and $50\text{mm}$ for $d$ in Equation (XXV).

    $\begin{array}{c}\sigma =\frac{32\times 4097\text{N}\cdot \text{m}}{\pi {\left(50\text{mm}\times \frac{1\text{m}}{1000\text{mm}}\right)}^3}\\ =333853594.5\text{Pa}\times \frac{1\text{MPa}}{{10}^6\text{Pa}}\\ =333.854\text{MPa}\\ \approx 333.9\text{MPa}\end{array}$

Substitute $3101\text{N}\cdot \text{m}$ for $T$ and $50\text{mm}$ for $d$ in Equation (XXVI).

    $\begin{array}{c}\tau =\frac{16\times 3101\text{N}\cdot \text{m}}{\pi {\left(50\text{mm}\times \frac{1\text{m}}{1000\text{mm}}\right)}^3}\\ =126345106.5\text{Pa}\times \frac{1\text{MPa}}{{10}^6\text{Pa}}\\ =1263.45\text{MPa}\\ \approx 126.3\text{MPa}\end{array}$

Substitute $333.9\text{MPa}$ for $\sigma$ and $126.3\text{MPa}$ for $\tau$ in Equation (XXVII).

    $\begin{array}{c}{\sigma }_1=\frac{333.9\text{MPa}}{2}+\sqrt{{\left(\frac{333.9\text{MPa}}{2}\right)}^2+{\left(126.3\text{MPa}\right)}^2}\\ =166.95\text{MPa}+209.34\text{MPa}\\ =376.3\text{MPa}\\ \approx 376\text{MPa}\end{array}$

Substitute $333.9\text{MPa}$ for $\sigma$ and $126.3\text{MPa}$ for $\tau$ in Equation (XXVIII).

    $\begin{array}{c}{\sigma }_2=\frac{333.9\text{MPa}}{2}-\sqrt{{\left(\frac{333.9\text{MPa}}{2}\right)}^2+{\left(126.3\text{MPa}\right)}^2}\\ =166.95-209.34\\ =-42.39\text{MPa}\\ \approx -42.4\text{MPa}\end{array}$

Substitute $333.9\text{MPa}$ for $\sigma$ and $126.3\text{MPa}$ for $\tau$ in Equation (XXIX).

    $\begin{array}{c}{\tau }_{\max }=\sqrt{{\left(\frac{333.9\text{MPa}}{2}\right)}^2+{\left(126.3\text{MPa}\right)}^2}\\ =209.3\text{MPa}\\ \approx \text{209}\text{MPa}\end{array}$

Refer to the Table A-20 “Deterministic ASTM Minimum Tensile and Yield Strengths for Some Hot-Rolled (HR) and Cold-Drawn (CD) Steels” and obtain $S_y=370\text{MPa}$ for $1018$ CD steel.

Substitute $376\text{MPa}$ for ${\sigma }_1$, $370\text{MPa}$ for $S_y$ and $-42.4\text{MPa}$ for ${\sigma }_2$ in the Equation (XXX).

    $\begin{array}{c}n=\frac{370\text{MPa}}{376\text{MPa}-\left(-42.4\text{MPa}\right)}\\ =0.884\\ \approx 0.88\end{array}$

Thus, the factor of safety for yielding from maximum-shear-stress theory is $0.88$.

Substitute $376\text{MPa}$ for ${\sigma }_1$, $370\text{MPa}$ for $S_y$ and $-42.4\text{MPa}$ for ${\sigma }_2$ in Equation (XXXII).

    $\begin{array}{c}n=\frac{370\text{MPa}}{{\left({\left(376\text{MPa}\right)}^2-\left(376\text{MPa}\right)\cdot \left(-42.4\text{MPa}\right)+{\left(-42.4\text{MPa}\right)}^2\right)}^{\frac{1}{2}}}\\ =0.927\\ \approx 0.93\end{array}$

Thus, the factor of safety for yielding from distortion-energy theory is $0.93$.